matlab中主函数调用fmincon函数，结果出问题

Posted 2023-05-13

function f=circle(R)
global R
x0=[2,1,0,0];
nonlcon=@circle1;
[x,feval]=fmincon(@circle2,x0,[],[],[],[],[],[],nonlcon);
function [c,ceq]=circle1(x)
global R
m=length(R);
for i=1:m
w(i)=i*2*3.1415/m
end
u=R.*cos(w);
v=R.*sin(w);
for i=1:m
c(i)=(u(i)-x(3))^2+(v(i)-x(4))^2-x(1)^2;
c(i+m)=-(u(i)-x(3))^2-(v(i)-x(4))^2+x(2)^2;
ceq=[];
end
function f=circle2(x)
f=x(1)-x(2);
Error in circle (line 2)
global j k

Output argument "f" (and maybe others) not assigned during call to "G:\Program
Files\MATLAB\bin\circle.m>circle".

参考技术A 软件卸掉了，所以无法回答

Matlab fmincon函数

文章目录

• • • • 函数功能
      • 函数表达及用法
      • • ==**trust-region-reflective算法的说明 (梯度)**==
        • **==Hessian矩阵应用说明==**
      • 返回值

函数功能

获取约束的非线性多变量函数的最小值
样式：

其中,c(x), ceq(x) 分别表示非线性的约束条件，而A, Aeq表示的是线性约束。

函数表达及用法

x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

1. fun
   minimizes fun
2. 初始值
   starts at x0，x0 can be a scalar, vector, or matrix.
3. 线性约束
   attempts to find a minimizer x of the function described in fun subject to the linear inequalities Ax ≤ b，Aeqx = beq，and the range lb ≤ x ≤ ub
4. 非线性约束
   the nonlinear inequalities c(x) or equalities ceq(x) defined in nonlcon
   For example,

   x = fmincon(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon)
   where mycon is a MATLAB function such as
   function [c,ceq] = mycon(x)
   c = ...     % Compute nonlinear inequalities at x.
   ceq = ...   % Compute nonlinear equalities at x.
   

5. 选项
   Optimization options, specified as the output of optimoptions or a structure such as optimset returns
   

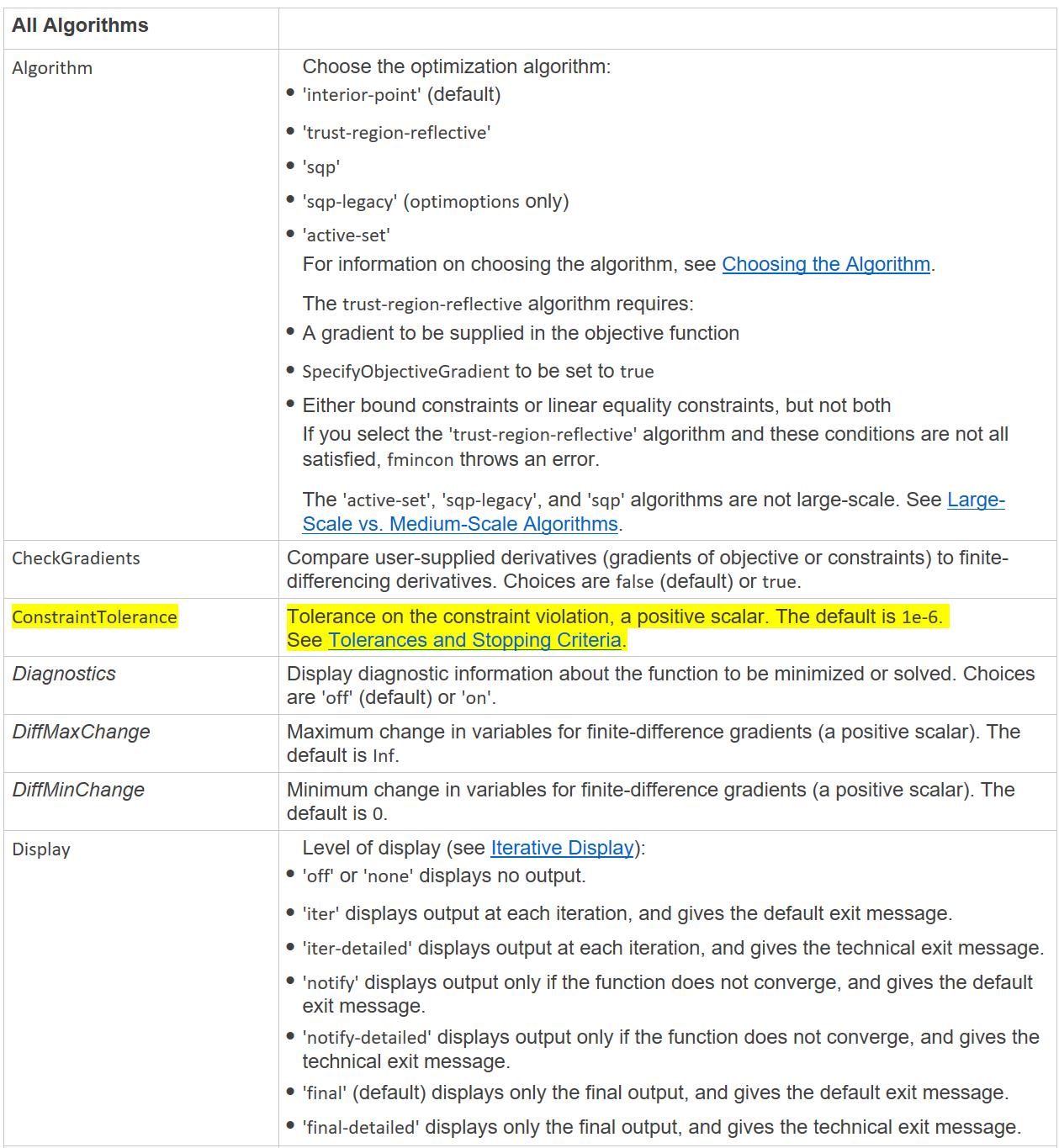
trust-region-reflective算法的说明 (梯度)

针对SpecialObjectiveGradient 将梯度计算加入目标函数中，以实现更快或更可靠的计算。将梯度计算作为条件化输出包含在目标函数文件中

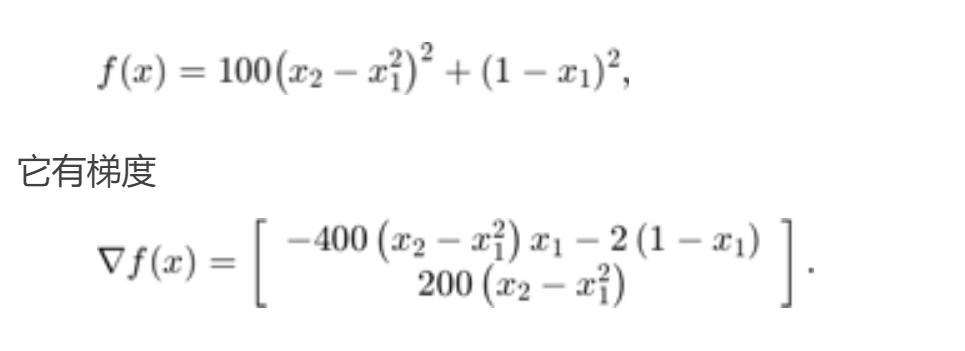
function [f,g] = rosenbrockwithgrad(x)
% Calculate objective f
f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;

if nargout > 1 % gradient required
    g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));
        200*(x(2)-x(1)^2)];
end

注：
1.目标函数（标量）作为第一个输出，梯度（向量）作为第二个输出（应该是默认的）
2.使用 optimoptions 将 SpecifyObjectiveGradient 选项设置为 true。如果有的化，也将 SpecifyConstraintGradient 选项设置为 true。

fun = @rosenbrockwithgrad;
x0 = [-1,2];
A = [];
b = [];
Aeq = [];
beq = [];
lb = [-2,-2];
ub = [2,2];
nonlcon = [];
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

调用

options = optimoptions('fmincon','SpecifyObjectiveGradient',true);

输出结果
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.


x =

    1.0000    1.0000

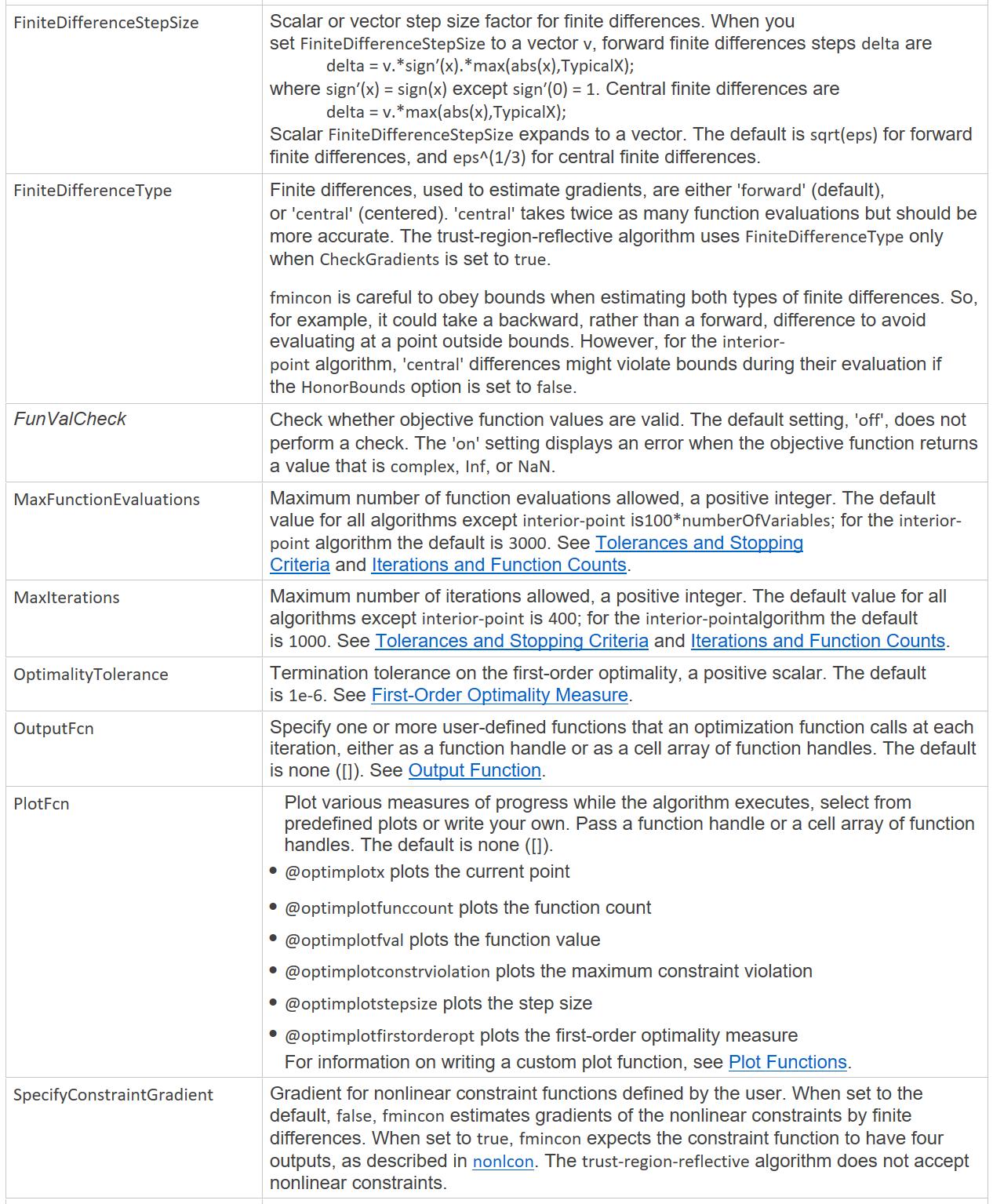
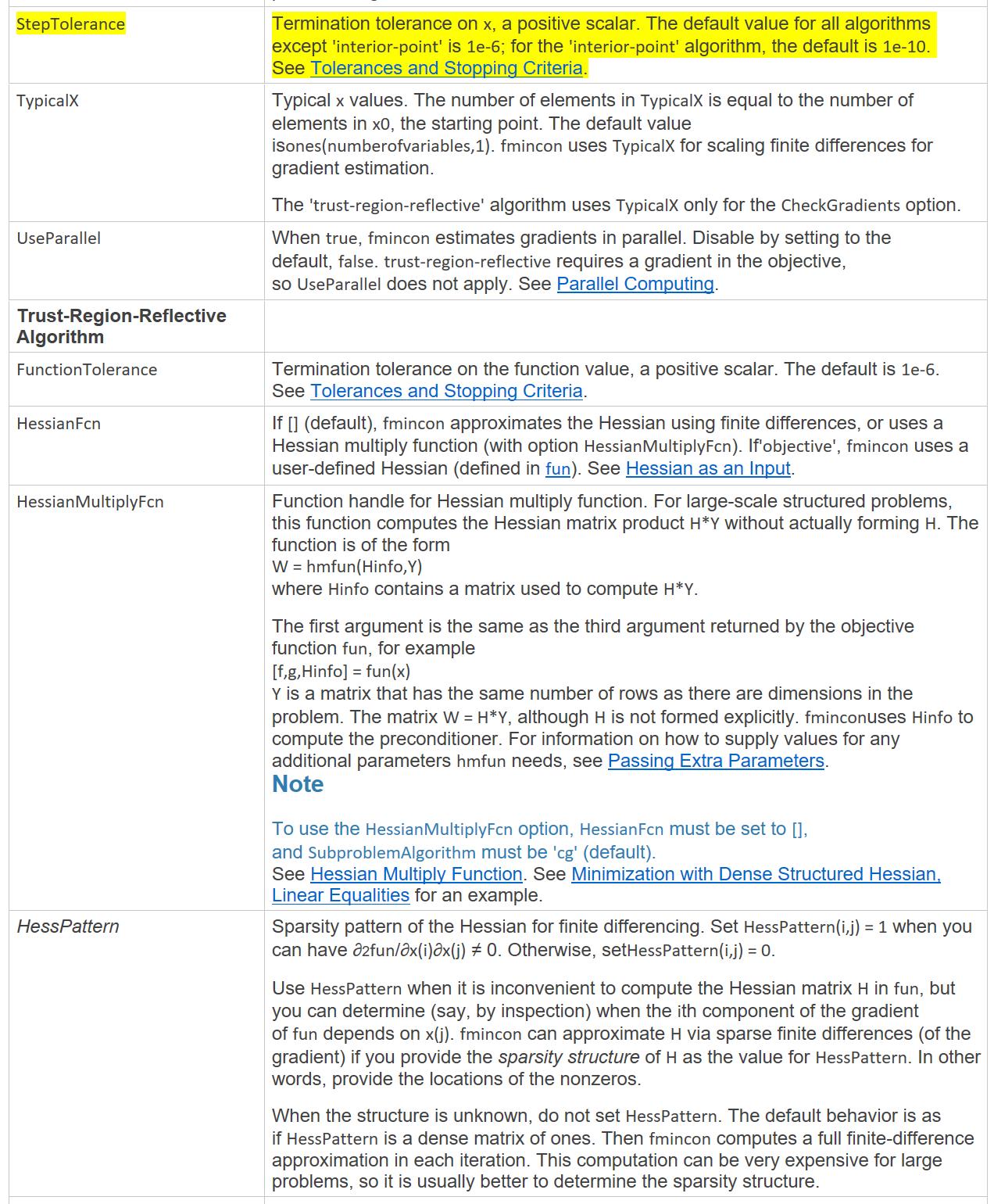
Hessian矩阵应用说明

上例代码修改为

function [f, g, H] = rosenboth(x)
% Calculate objective f
f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;

if nargout > 1 % gradient required
    g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));
        200*(x(2)-x(1)^2)];
    
    if nargout > 2 % Hessian required
        H = [1200*x(1)^2-400*x(2)+2, -400*x(1);
            -400*x(1), 200];  
    end

end

注：
1.使用 fmincon ‘trust-region-reflective’ 和 ‘interior-point’ 算法以及 fminunc ‘trust-region’ 算法来包含二阶导数。根据信息的类型和算法，可通过几种方法来包括 Hessian 矩阵信息。
2. 您还必须包含梯度（将 SpecifyObjectiveGradient 设置为 true，如果适用，还必须将 SpecifyConstraintGradient 设置为 true）以便包含 Hessian 矩阵
调用：

options = optimoptions('fminunc','Algorithm','trust-region',...
    'SpecifyObjectiveGradient',true,'HessianFcn','objective');

适用于 fmincon 内点算法的 Hessian 矩阵. 该 Hessian 矩阵是拉格朗日函数的 Hessian 矩阵，其中 L(x,λ) 是

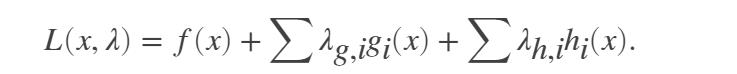
g 和 h 是向量函数，分别表示所有不等式和等式约束（指有界、线性和非线性约束），因此最小化问题的公式为

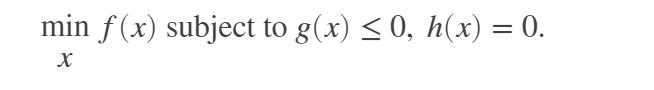
拉格朗日方程的 Hessian 矩阵公式为：

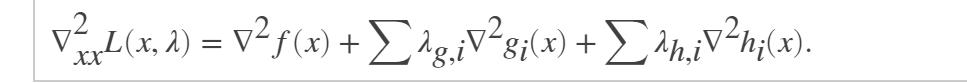
ssian 是 n×n 矩阵（稀疏或稠密），其中 n 是变量的数目。如果 hessian 很大并且非零项相对较少，请将 hessian 表示为稀疏矩阵，以节省运行时间和内存。lambda 是具有与非线性约束相关联的拉格朗日乘数向量的结构体：

lambda.ineqnonlin
lambda.eqnonlin
fmincon 计算结构体 lambda，并将其传递给您的 Hessian 函数。hessianfcn 必须计算上式中的总和。通过设置以下选项表明您提供了 Hessian 函数：

ptions = optimoptions('fmincon','Algorithm','interior-point',...
    'SpecifyObjectiveGradient',true,'SpecifyConstraintGradient',true,...
    'HessianFcn',@hessianfcn);

function Hout = hessianfcn(x,lambda)
% Hessian of objective
H = [1200*x(1)^2-400*x(2)+2, -400*x(1);
            -400*x(1), 200];
% Hessian of nonlinear inequality constraint
Hg = 2*eye(2);
Hout = H + lambda.ineqnonlin*Hg;

将 hessianfcn 保存到 MATLAB 路径。为了完成此示例，包含梯度的约束函数为

function [c,ceq,gc,gceq] = unitdisk2(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];

if nargout > 2
    gc = [2*x(1);2*x(2)];
    gceq = [];
end

调用：

fun = @rosenboth;
nonlcon = @unitdisk2;
x0 = [-1;2];
options = optimoptions('fmincon','Algorithm','interior-point',...
    'SpecifyObjectiveGradient',true,'SpecifyConstraintGradient',true,...
    'HessianFcn',@hessianfcn);
[x,fval,exitflag,output] = fmincon(fun,x0,[],[],[],[],[],[],@unitdisk2,options);

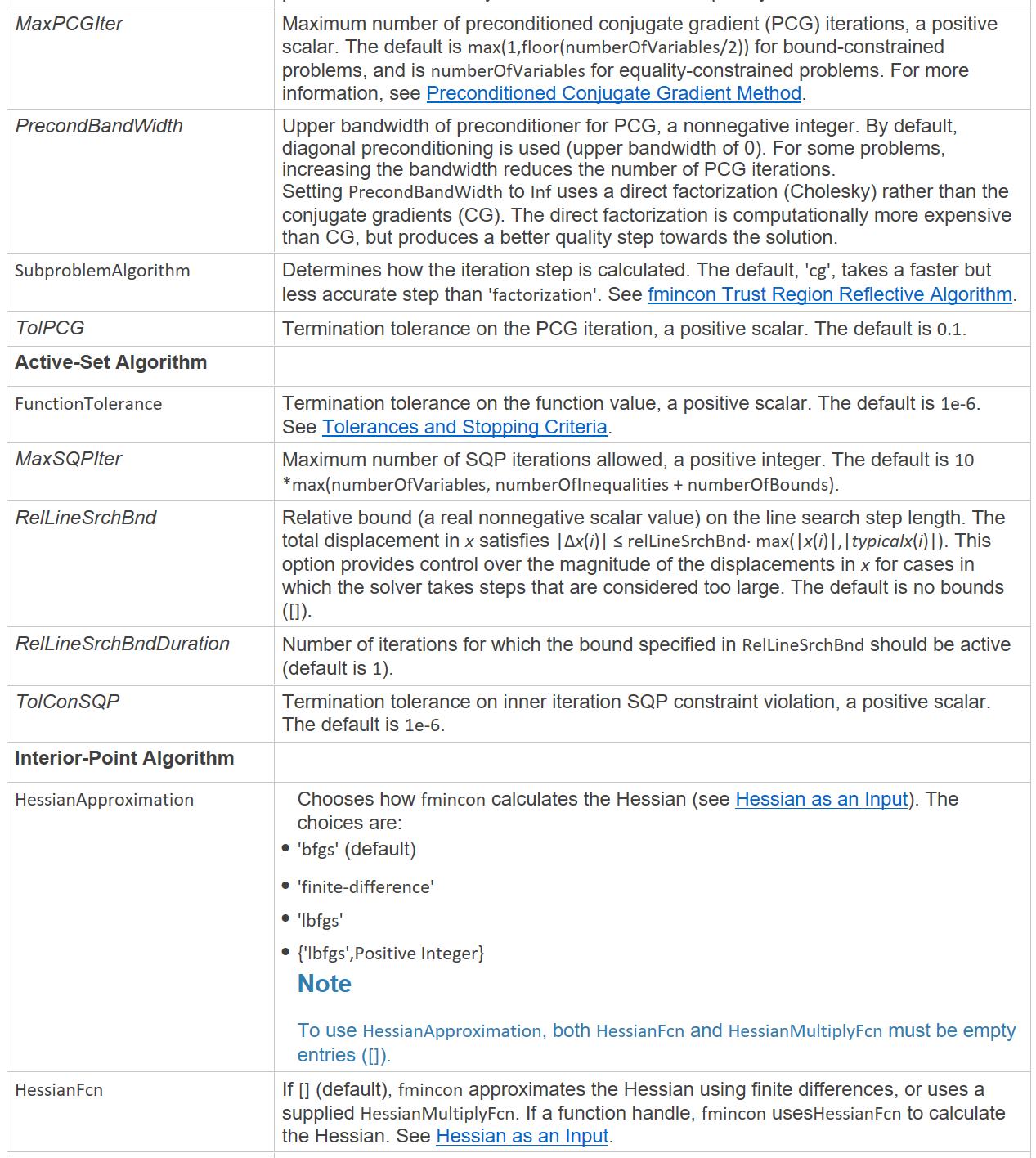
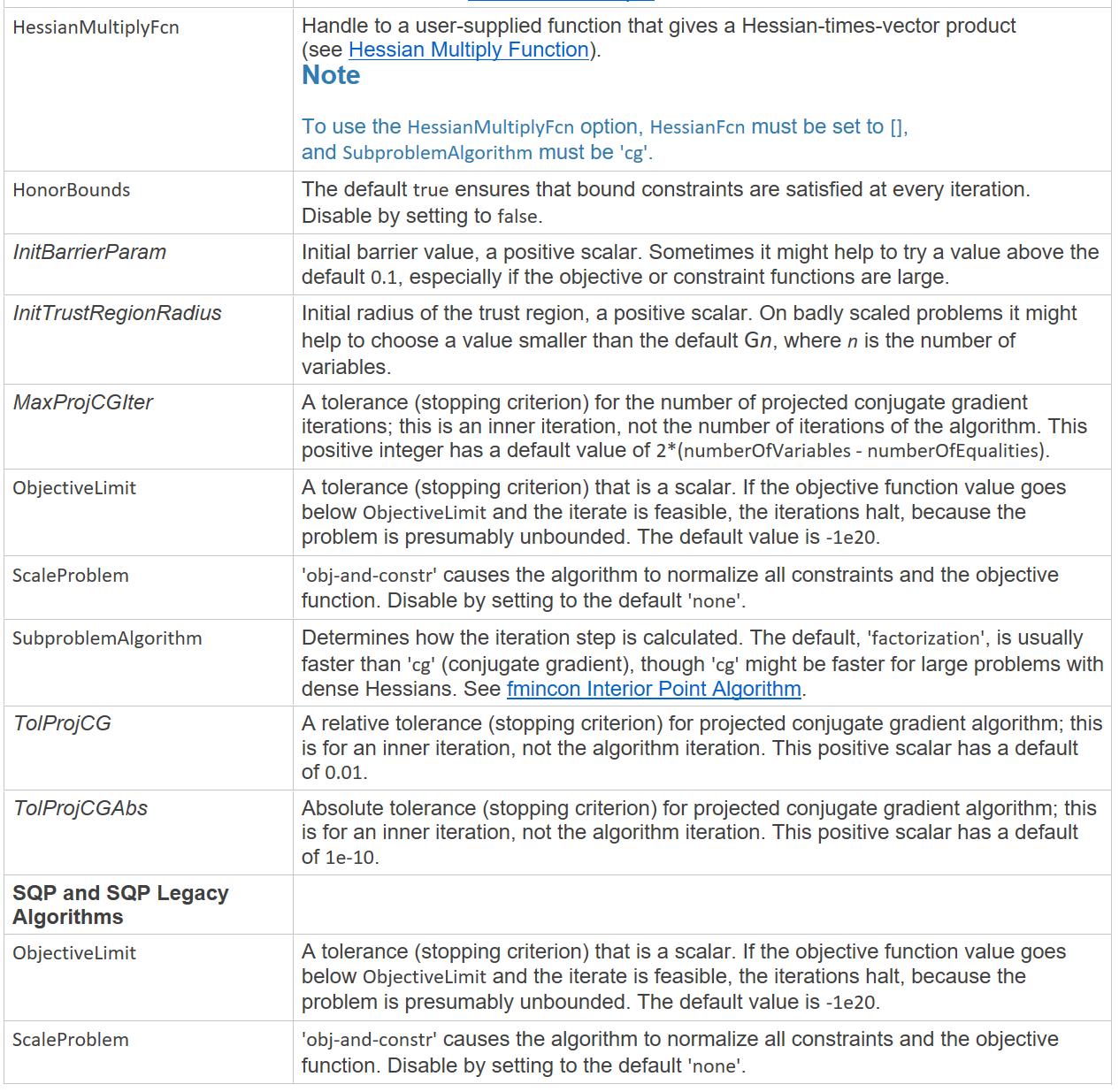
6. Algorithm
   

返回值

[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(___) additionally returns:

x— variable
fval— the value of the objective function fun
exitflag— describes the exit condition of fmincon,
output— a structure output with information about the optimization process.
lambda — Structure with fields containing the Lagrange multipliers at the solution x.
grad — Gradient of fun at the solution x.
hessian — Hessian of fun at the solution x. See fmincon Hessian.

有关拉格朗日算子到底是啥，可参考：如何理解拉格朗日乘子法？
梯度和海森矩阵请参考：牛顿法与拟牛顿法学习笔记

1. exitflag
   
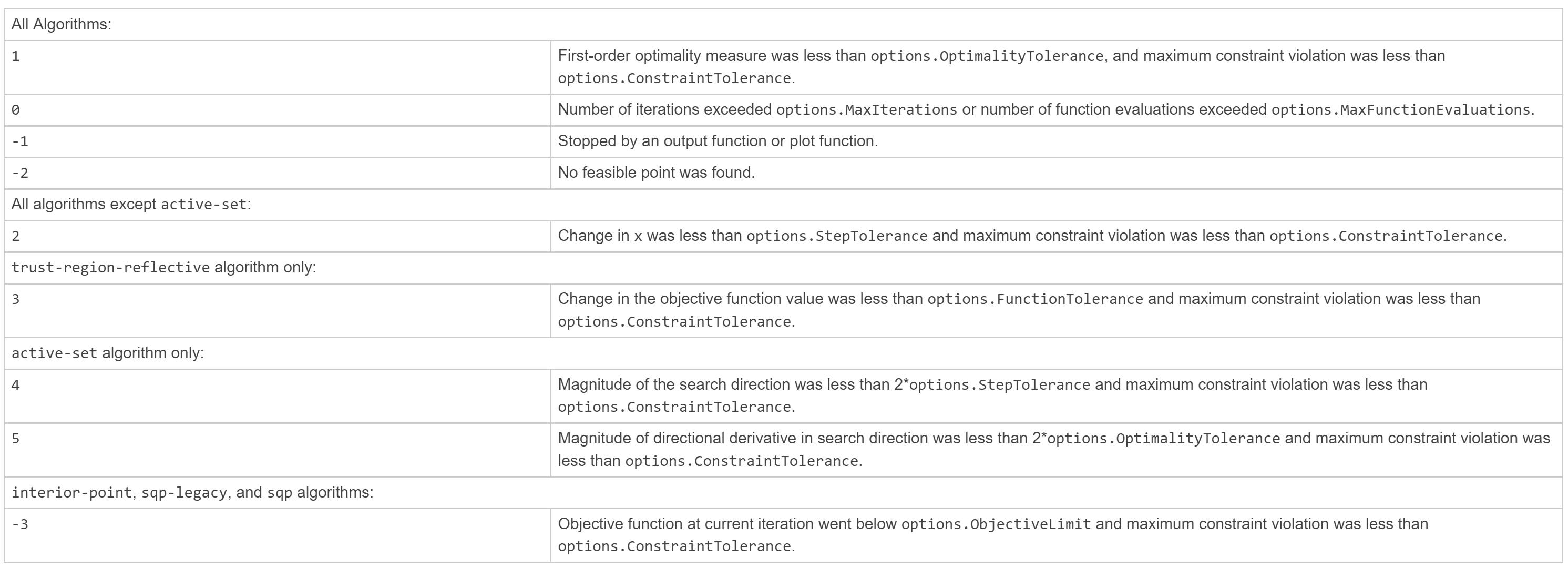
2. output
   
3. lambda
   
4. Hessian