树状数组--动态维护区间操作

Posted 2023-05-12 xuan01

树状数组 (二元索引树 / 二元下标树 / Binary Indexed Tree, BIT / Fenwick Tree): 树状数组虽名为数组，但从其英文名 (Binary Indexed Tree) 可看出它本质上是一种被表达为树的数据结构。对于大小为n 的序列nums ，最基本的树状数组以O(logn) 时间复杂度同时支持如下两种操作。

1）更新nums 中单个元素的值，即 单点修改(Point Update) 。

2）求nums 任意区间的元素值之和，即 区间查询(Range Query) 。

数组：对于单点修改：数组可以利用下标直接修改，O(1),但是对于区间查询则为O(N)；

前缀和：对于区间查询，前缀和可以做到O(1)，但是对于单点修改，需要修改该点以后的所有前缀和数值，O(N)；

学习视频摘自：〔manim | 算法 | 数据结构〕 完全理解并深入应用树状数组 | 支持多种动态维护区间操作_哔哩哔哩_bilibili

学习博客摘自：树状数组从入门到下车 - 力扣（LeetCode）

 

lowbit操作：

t [ ] 数组：

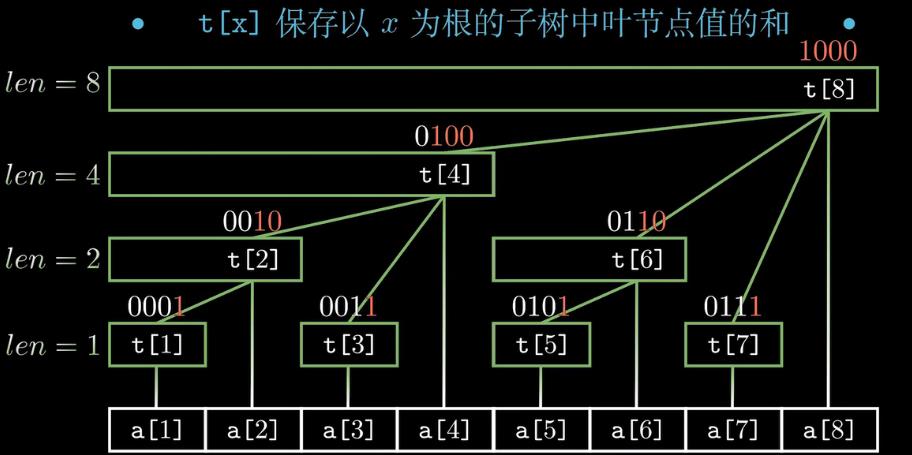
单点修改、区间查询：

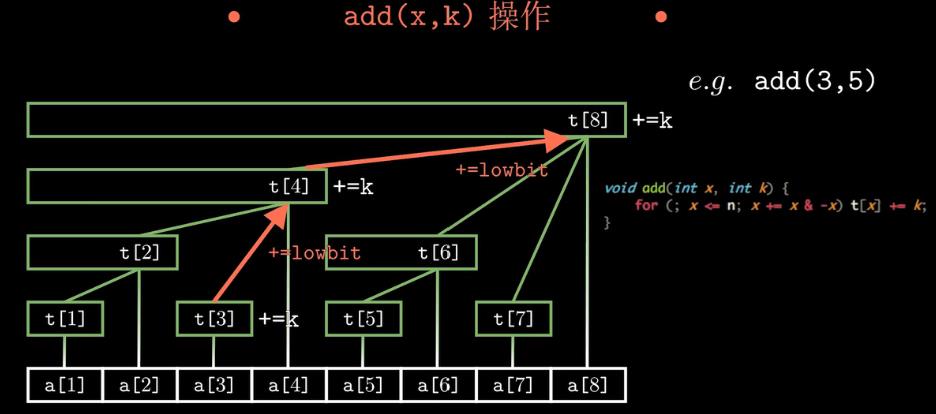
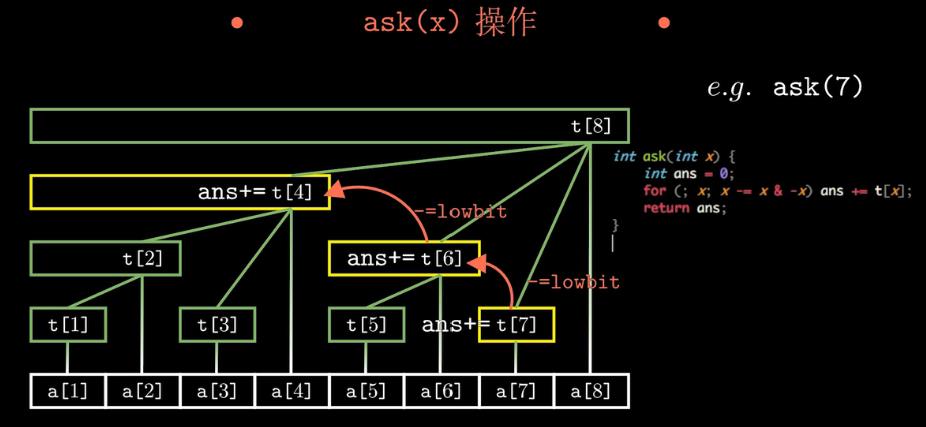
区间修改、单点查询：

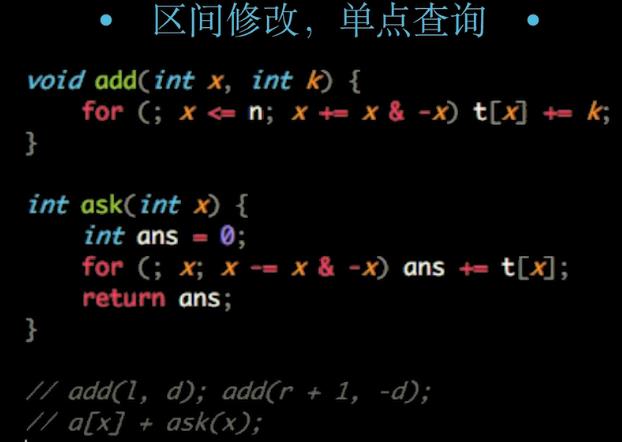
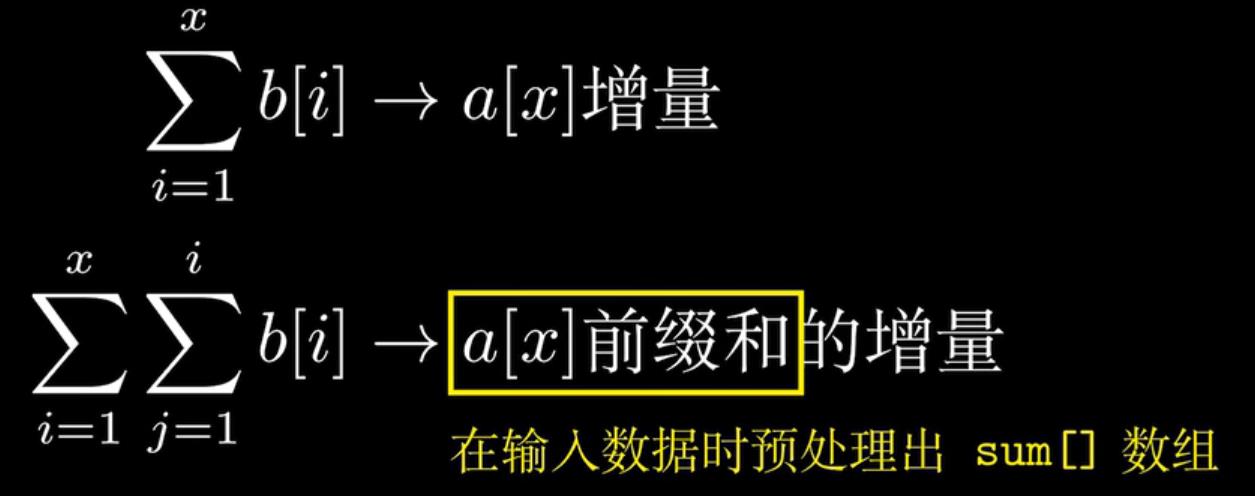
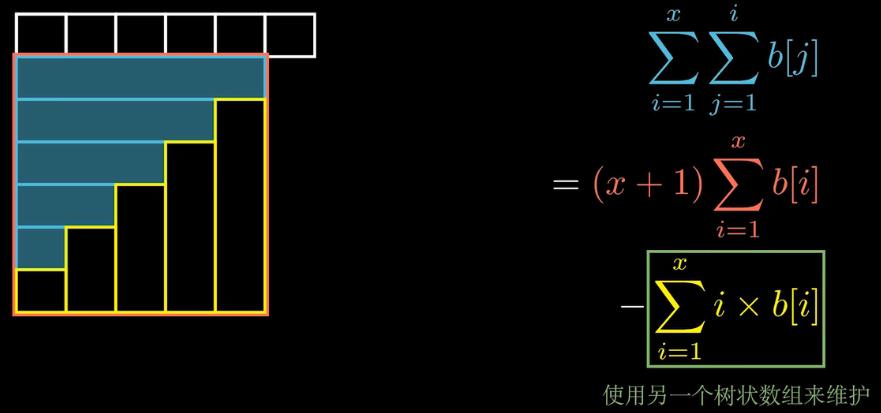
区间修改、区间查询：

整个矩形面积，减去黄色面积；

注意这儿是  前缀和的增量；

 

动态求区间K大值（权值线段树）

我们知道我们可以通过主席树来维护静态区间第K大值。我们又知道主席树满足可加性，所以我们可以用树状数组来维护主席树，树状数组的每一个节点都可以开一颗主席树，然后一起做。

我们注意到树状数组的每一棵树都和前一颗树没有关系，so，并不需要可持久化，一个朴素的权值线段树就可以啦。

我们知道普通的线段树是刚开始就把所有的节点都开了，但我们发现并不需要，因为每个点里的操作并不是很多，很大一部分的节点是用不到的，那么我们就可以不开。用Ls 和 Rs 来记左右儿子的地址，随用随开即可。

#include<bits/stdc++.h>
#define N 100005
#define mid ((l+r)>>1)
using namespace std;
inline int lowbit(int x){return x&-x;}
int n,m,sz,totn,totx,toty,a[N],b[N<<1],ca[N],cb[N],cc[N];
int xx[N],yy[N],rt[N],size[100*N],ls[100*N],rs[100*N];
void ins(int l,int r,int x,int q,int v){
    size[x]+=v;
    if (l==r) return;
    if (q<=mid) { if (!ls[x]) ls[x]=++sz; ins(l,mid,ls[x],q,v);
    } else { if (!rs[x]) rs[x]=++sz; ins(mid+1,r,rs[x],q,v);    
    }
}
int query(int l,int r,int q){
    if(l==r)return l; int sum=0;
    for(int i=1;i<=totx;i++)sum-=size[ls[xx[i]]];
    for(int i=1;i<=toty;i++)sum+=size[ls[yy[i]]];
    if(q<=sum){
        for(int i=1;i<=totx;i++)xx[i]=ls[xx[i]];
        for(int i=1;i<=toty;i++)yy[i]=ls[yy[i]];
        return query(l,mid,q);
    }
    else{
        for(int i=1;i<=totx;i++)xx[i]=rs[xx[i]];
        for(int i=1;i<=toty;i++)yy[i]=rs[yy[i]];
        return query(mid+1,r,q-sum);
    }
}
void add(int x,int v){
    int k=lower_bound(b+1,b+totn+1,a[x])-b;
    for(int i=x;i<=n;i+=lowbit(i))ins(1,totn,rt[i],k,v);
}
inline int read(){
    int f=1,x=0;char ch;
    do{ch=getchar();if(ch==‘-‘)f=-1;}while(ch<‘0‘||ch>‘9‘);
    do{x=x*10+ch-‘0‘;ch=getchar();}while(ch>=‘0‘&&ch<=‘9‘);
    return f*x;
}
int main(){char s[20];
    n=read();m=read();
    for(int i=1;i<=n;i++)a[i]=read(),b[++totn]=a[i];
    for(int i=1;i<=m;i++){
        scanf("%s",s);ca[i]=read();cb[i]=read();
        if(s[0]==‘1‘)cc[i]=read();else b[++totn]=cb[i];
    }
    sort(b+1,b+totn+1);
    totn=unique(b+1,b+totn+1)-b-1;
    for (int i=1;i<=n;i++) rt[i]=i; sz=n;
    for(int i=1;i<=n;i++)add(i,1);
    for(int i=1;i<=m;i++){
        if(cc[i]){
            totx=toty=0;
            for(int j=ca[i]-1;j;j-=lowbit(j))xx[++totx]=rt[j];
            for(int j=cb[i];j;j-=lowbit(j))yy[++toty]=rt[j];
            printf("%d\n",b[query(1,totn,cc[i])]);
        }
        else{add(ca[i],-1);a[ca[i]]=cb[i];add(ca[i],1);}
    }
}

就酱紫。