3853 -- 三只企鹅

Posted 2023-05-11 happy-XQJ

题目大意：
- 给定一棵 n 个点的树，然后有 m 个操作，分为修改操作和查询操作。
- 修改操作：金企鹅向点 u 空投零食，其他每个点产生快递费，快递费等于 u 到该点的距离。
- 查询操作：金企鹅想询问点 u 至今为止产生的快递费。

------------

题解：对于修改操作，每次选一个点，所有点的权值加上到该点的距离，如果暴力修改显然超时。

我们可以先考虑这样一个问题： 选择出点u，那么一个指定点v产生的贡献是多少？答案是 : $dep[u]+dep[v]-2*dep[lca(u,v)]$

这是一对点，如果多次修改呢？

显然我们可以把上面式子拆成两个部分设某次查询操作之前选了这些点空头： $s_1$ , $s_2$ , $s_3$ ,....., $s_n$

那么 $dep[u]$ 就是: $\\sum_i=1^ndep[s_i]$ $\\ $ 这个可以记下来。

 $\\qquad $ $dep[v]$ 就是：$n*dep[v]$ $\\ $ 这个可以查询的时候直接计算
 
 那么剩下我们就只需要统计： $ 2*\\sum_i=1^ndep[lca(s_i,v)] $ 就是所有的 $lca$ 的深度和。
 
 你发现一个点的深度其实是这个点到根节点上所有的边权和，两个点的 $lca$ 的深度就是重合部分，我们考虑把边权下放到点上，那选出点时就可以把这个点到根节点上所有的点都加上相对应的边权，查询的时候就是求出这个点到根节点上所有的权值和。问题就转化成了树上一条链上区间加和区间求和，很自然的想到**树链剖分**。
 
 最后线段树你可能会对状态的设置产生一些疑问，可以设 $s$ 表示总和， $sum$ 表示对应的点权（边权）和， $lazy$ 表示这个区间加了多少次，每次 $pushdown$ 的时候就 $s+=sum*lazy$ 表示直接加上这个区间。本题就做完了。附代码。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,m;
struct stu
  int y,z;
;
vector<stu>p[200005];
long long dd[200005];
int dep[200005];
int siz[200005],son[200005],tp[200005],fa[200005],id[200005],rk[200005],tot=0;
int qz[200005];
void dfs1(int i,int ff)
  fa[i]=ff;
  dep[i]=dep[ff]+1;
  siz[i]=1;
  for(int j=0;j<p[i].size();j++)
    int to=p[i][j].y,val=p[i][j].z;
    if(to==ff)continue;
    qz[to]=val;
    dd[to]=dd[i]+val;
    dfs1(to,i);
    siz[i]=siz[i]+siz[to];
    if(siz[to]>siz[son[i]])son[i]=to;
  

void dfs2(int i,int top)
  tp[i]=top;
  id[i]=++tot;
  rk[tot]=i;
  if(son[i])dfs2(son[i],top);
  for(int j=0;j<p[i].size();j++)
    int to=p[i][j].y;
    if(to==son[i]||to==fa[i])continue;
    dfs2(to,to);
  

long long ans1=0,gs=0,ans2=0;
long long sum[200005*4],lazy[200005*4],tree[200005*4];
void build(int k,int l,int r)
  if(l==r)
    sum[k]=qz[rk[l]];
    return;
  
  int mid=(l+r)/2;
  build(k*2,l,mid);
  build(k*2+1,mid+1,r);
  sum[k]=sum[k*2]+sum[k*2+1];

void pushdown(int k)
  if(lazy[k])
    lazy[k*2]+=lazy[k];
    lazy[k*2+1]+=lazy[k];
    tree[k*2]+=sum[k*2]*lazy[k];
    tree[k*2+1]+=sum[k*2+1]*lazy[k];
    lazy[k]=0;
  

void xg(int k,int l,int r,int L,int R,int val)
  if(l>R||r<L)return;
  if(l>=L&&r<=R)
    lazy[k]++;
    tree[k]+=sum[k];
    return;
  
  pushdown(k);
  int mid=(l+r)/2;
  xg(k*2,l,mid,L,R,val);
  xg(k*2+1,mid+1,r,L,R,val);
  tree[k]=tree[k*2]+tree[k*2+1];

long long query(int k,int l,int r,int L,int R)
  if(l>R||r<L)return 0;
  if(l>=L&&r<=R)return tree[k];
  pushdown(k);
  int mid=(l+r)/2;
  long long res=0;
  res=res+query(k*2,l,mid,L,R);
  res=res+query(k*2+1,mid+1,r,L,R);
  return res;

void change(int x,int y,int u)
  while(tp[x]!=tp[y])
    if(dep[tp[x]]<dep[tp[y]])swap(x,y);
    xg(1,1,n,id[tp[x]],id[x],dd[u]);
    x=fa[tp[x]];
  
  if(id[x]>id[y])swap(x,y);
  xg(1,1,n,id[x],id[y],dd[u]);

long long qquery(int x,int y)
  long long res=0;
  while(tp[x]!=tp[y])
    if(dep[tp[x]]<dep[tp[y]])swap(x,y);
    res=res+query(1,1,n,id[tp[x]],id[x]);
    x=fa[tp[x]];
  
  if(id[x]>id[y])swap(x,y);
  res=res+query(1,1,n,id[x],id[y]);
  return res;

int main()
  // freopen("4.in","r",stdin);
  // freopen("4.out","w",stdout);
  scanf("%d%d",&n,&m);
  for(int i=1;i<n;i++)
    int n1,n2,n3;
    scanf("%d%d%d",&n1,&n2,&n3);
    p[n1].push_back((stu)n2,n3);
    p[n2].push_back((stu)n1,n3);
  
  dfs1(1,1);
  dfs2(1,1);
  build(1,1,n);
  while(m--)
    int opt,u;
    scanf("%d%d",&opt,&u);
    if(opt==1)
      gs++;
      ans1=ans1+dd[u];
      change(u,1,u);
    else 
      ans2=ans1+gs*dd[u];
      ans2=ans2-2*qquery(u,1);
      printf("%lld\\n",ans2);
    
  
  return 0;

 

本题和1988染色本质一样，只是1988一个点只能贡献一次，所以需要开个数组记一下防止加重。（~~双倍经验~~）

干掉这三只“拦路虎”，OpenStack妥了

云计算是一种计算模型，它将诸如运算能力、存储、网络和软件等资源抽象成为服务，用户可通过互联网远程连接并使用；因需而定、提供方便、动态改变和无限的虚拟化扩展能力是云计算的几个重要特征。

OpenStack是现在实现云计算平台非常热门的一种技术实现方式，市场上有非常多的基于OpenStack二次开发的云平台产品。而如何保证为OpenStack提供一个稳定、快速的集群云存储产品，需要解决以下三只“拦路虎”：

如何在OpenStack环境下实现存储的高性能

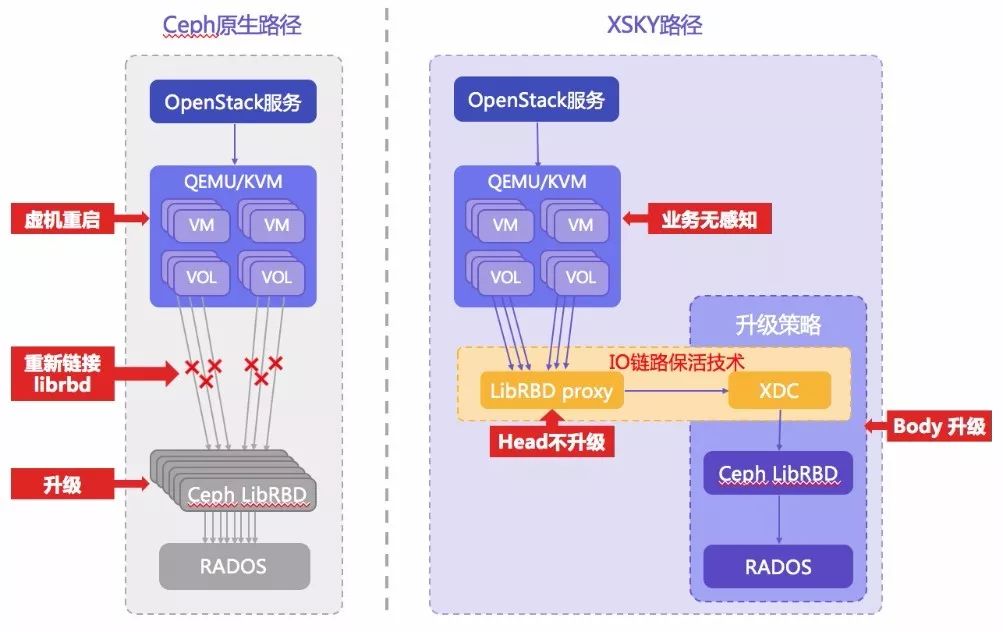
在Ceph对接OpenStack的原生路径中，当虚机挂载卷的时候，每打开一个卷会独占1个RBD连接通道供自己使用，每个RBD通道都具备完整的Ceph Client资源，连接所需要的OSD，这样每个RBD通道都需要占一定量的系统资源(数百TCP连接，几十MB的内存以及额外CPU利用)；如果卷数量少的情况下，往往看不出性能问题，但是真实业务场景下，虚机的数量往往非常多，这样随着访问卷的数目增加，RBD通道数目也会相应增加，这都需要占用更多的内存和CPU的资源，导致整个存储的性能急剧下降。同时，随着 OSD 数目的增多，所有通道都会增加资源消耗，带来极大的系统资源负担，这些真实损耗往往就是辛辛苦苦虚拟化后带来的价值。经常可以看到在生产环境计算节点消耗了上千个线程和TCP连接用于每个QEMU进程，正是因为RBD的消耗算在了QEMU头上，很多用户难以发现背后的问题。除此之外，每个RBD通道对于Ceph集群都是独立客户端，对于Monitor也是负担，大量客户端极大限制了单池的扩展能力。

为了解决资源消耗问题，XSKY自研了具有专利技术的XDC模块，提供LibRBD proxy代理，通过代理劫持客户端访问RBD的命令，将无序的访问命令统一管理起来，根据系统资源使用情况按需打开RBD通道，从而达到资源的有效管理。

举个例子：没有经过优化前，如果集群中某个计算节点运行有50个虚机，每个虚拟机打开2个卷，则需要生成100个连接通道，每一个通道启动20多个线程，系统中将出现2000多个线程抢占CPU资源的情况，导致系统性能显著下降，而经过XSKY的优化后，XDC会根据系统资源使用情况自动按需打开若干个连接通道，这样整个存储平台性能在OpenStack场景下有了显著改善。

如何在OpenStack环境下实现业务无感知的存储在线升级

存储设备作为整个云计算平台的数据支撑，其产品正常的软件升级迭代是必不可少的，Ceph的存储产品需要通过原生路径，即QEMU来连接RBD库，所以存储产品升级时Ceph RBD必须要重新启动，QEMU才能完成对新RBD库的连接，这个过程虚拟机必须宕机，影响业务持续性。由于整个RBD Client非常庞大，包含了所有资源和逻辑，所以当发现重大的客户端BUG时，Ceph的升级虽然很容易，但是客户端的库链接成了巨大的累赘，在某些版本中，用户不得不停机所有QEMU进程进行库重新链接升级。这也使得一些客户端优化和功能无法应用到虚拟机上，失去了日益完善的存储集群升级优化的意义。

XSKY 提供“Head-Body”升级技术能保证升级过程中业务无感知，其中只用作IO转发的LibRBD proxy 作为“head”被链接到QEMU中，这部分的使用和Ceph原有方式一致，但是在升级过程中保持不变，无需更新；实现主要功能的XDC作为“body”可以跟随版本自由升级，在升级过程中XDC具备的“IO链路保活技术”能保证IO的持续性，使存储升级对前端在线业务无感知。

如何便捷的对多云平台进行统一监控

云场景下，不同的虚拟化管理平台如 VMware VCenter、OpenStack 和 ZStack 都可以对接同一个存储池，实现容量、IO资源的虚拟化统一调度。

XSKY 云集成管理功能，不仅能够将资源池化应用到不同的云平台，而且还能将 OpenStack 添加到 XSKY 管理面板中，实现在同一个界面下对于不同虚拟化类型情况下，以虚拟机角度的 IO 性能和容量监控，极大方便了存储管理员对于虚拟化场景使用的管理。

另外，XSKY 管理平台还支持对接 OpenStack KeyStone，利用 KeyStone 作为统一认证系统，提高了与 OpenStack 的粘合度。

XSKY 分布式软件定义存储为OpenStack用户带来的价值

存储性能的整体提升：XSKY产品针对OpenStack的性能优化，帮助用户实现了一台存储设备可以支持更多的云端业务；

便捷的产品升级方式：XSKY产品具有独创的“IO链路保活技术”帮助用户实现在OpenStack下对前端业务无感知的存储在线升级，实现业务的7x24高可靠性；

敏捷运维，高效管理：在同一套系统中提供完整数据服务能力，大大降低了运维管理成本；提供友好的管理工具，提升管理效率，同时可以将存储和云端管理集成到统一管理平台中，使得运维更加敏捷、高效。

经过实测，XSKY分布式SDS在OpenStack场景下为客户带来了如下收益：

单客户端4K随机写IOPS提升20%；

客户端IO延迟降低15%；

每节点CPU利用率降低40%；

每节点存储部分内存使用减少2/3；

人力维护工作量减少30%。

XSKY实现了对社区版本的LibRBD接口100%兼容，使用时只需修改库引用路径即可。不仅支持全系列版本的OpenStack，也可无缝对接CloudStack和ZStack。

应用实践

XSKY已协助东吴证券，光大证券，景芝酒业，某军工云网，某省级电信等多家客户成功对接基于KVM的云平台，在成本下降的同时基于KVM的云平台性能得到了大幅提升，为用户快速构建高效、稳定、可靠的云数据中心环境提供了有力支撑。

点击下方“往期推荐”更多精彩与您分享！

↓↓↓

☞ 往期推荐：

• 
  

• 
  

•