fisher判别方法的主要特点是

Posted 2023-03-09

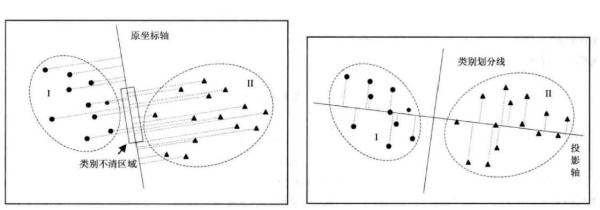
参考技术A

fisher判别方法的主要特点是先对数据进行投影然后再利用距离进行判别。

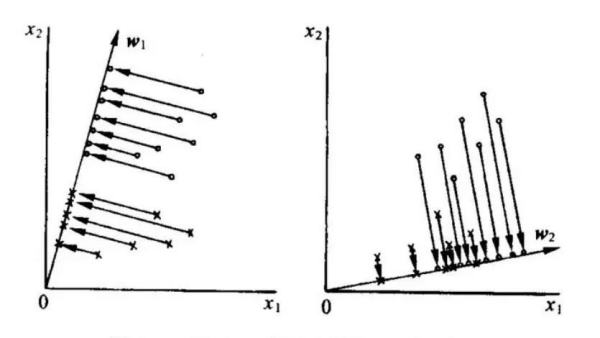
Fisher判别法是判别分析的方法之一，它是借助于方差分析的思想，利用已知各总体抽取的样品的p维观察值构造一个或多个线性判别函数y=l′x其中l= (l1，l2…lp)′，x= (x1，x2，…，xp)′，使不同总体之间的离差(记为B)尽可能地大，而同一总体内的离差(记为E)尽可能地小来确定判别系数l=(l1，l2…lp)′。数学上证明判别系数l恰好是|B-λE|=0的特征根，记为λ1≥λ2≥…≥λr>0。所对应的特征向量记为l1，l2，…lr，则可写出多个相应的线性判别函数，在有些问题中，仅用一个λ1对应的特征向量l1所构成线性判别函数y1=l′1x不能很好区分各个总体时，可取λ2对应的特征向量l′2建立第二个线性判别函数y2=l′2x，如还不够，依此类推。有了判别函数，再人为规定一个分类原则(有加权法和不加权法等)就可对新样品x判别所属。