C/C++交通咨询系统设计哈夫曼编码问题[2023-05-11]

Posted 2023-05-11 codewriter

C/C++交通咨询系统设计哈夫曼编码问题[2023-05-11]

题目三、交通咨询系统设计

最短路径问题
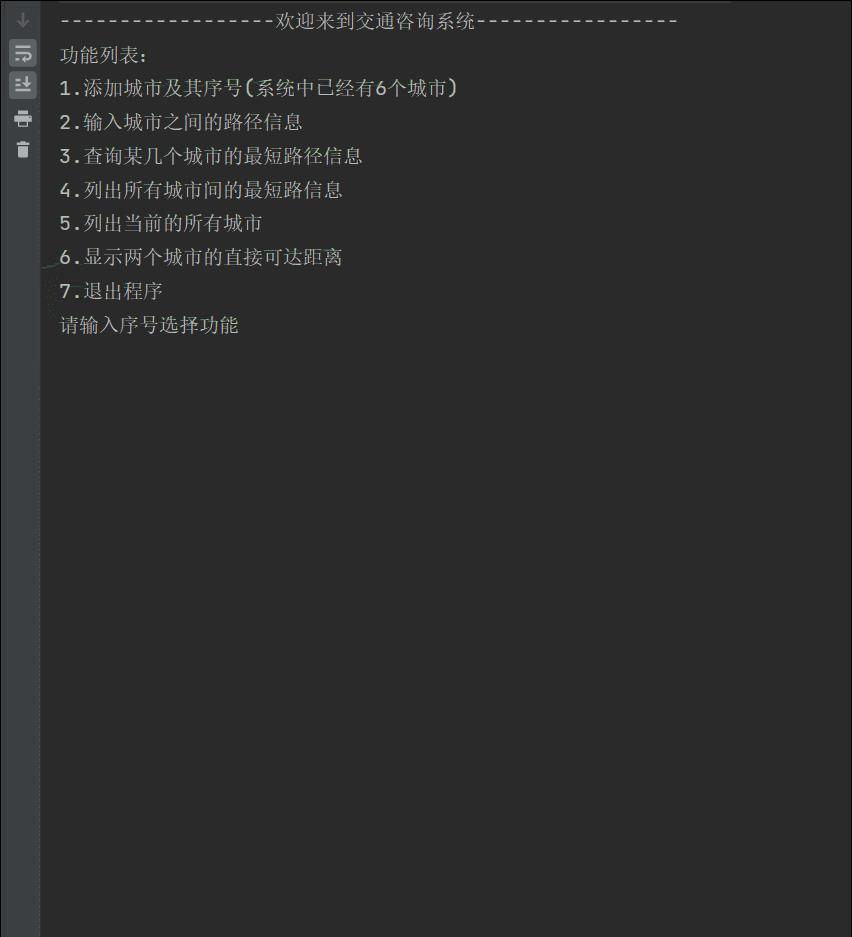
设计要求及分析:
设计一个交通咨询系统，能让旅客咨询从任一个城市顶点到另一城市顶点之间的最短路径(里程) 、最低花费、最少时间等问题。
对于不同咨询要求，可输出城市间的路程、所需时间、所需费用。

交通咨询系统设计

实现要求:

• 建立交通网终图的存储结构 (邻接矩阵、邻接表)；
• 解决单源最短路径问题(评估从一个城市出发到其余所有城市的最短路径规划，Dijkstra算法);
• 实现两个城市顶点之间的最短路径问题(两城市间的最短路径规划，Floyd算法，有加分)。

题目六、哈夫曼编码问题

设计内容:对输入的一串电文字符实现哈夫曼编码，再对哈夫曼编码生成的代码串进行译码，输出电文字符串。

实现功能:
(1)根据输入的字符串，统计每种字符的出现概率，以此为基础完成对应哈夫曼树的建立;
(2)哈夫曼编码的生成;
(3)从文件中读入需要译码的串，完成译码。

设计要求:
(1)三个功能模块要求用函数的形式实现。
(2)以菜单的方式选择编码或者译码。

源码

https://pan.baidu.com/s/1pq1Nwwo0hlc_J84F93HM4A?pwd=1111

太原理工大学2021数据结构课程设计(交通咨询系统（最短路径问题）)

太原理工大学数据结构课程设计(交通咨询系统（最短路径问题）)

声明：这里只是给出核心代码

核心代码指程序的计算部分，不是完整程序

背景题目

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 i号点到 j 号点的最短距离，如果无法从 i 号点走到 j 号点，则输出 −1。

输入格式

第一行包含三个整数n，m，k

接下来 m 行每行包含三个整数x,y,z，表示存在一条从点 x 到点 y的有向边，边长为 z。

接下来k行，每行包含两个整数i，j，表示询问点i到点j的最短距离。

输出格式

共k行，每行输出一个整数，表示i到j的最短路，若询问两点间不存在路径，则输出“impossible”

数据范围

1≤n≤5001≤n≤500,
1≤m≤1051≤m≤105,
图中涉及边长均不超过10000。

输入样例：

3 3 2
1 2 2
2 3 1
1 3 4
1 2
2 3

输出样例：

2 
1

题目背景知识

1.这是一个经典的多源最短路Floyd算法

2.思路是动态规划

3.无向图的邻接矩阵是对称的，与有向图的区别是，读入的时候对称的填入数据即可

Floyd算法代码(java)

import java.io.*;

/**
 * @see 图论 多源最短路 Floyd求最短路 https://www.acwing.com/solution/content/20441/
 */

public class Main {
        /*解题思路，动态规划的思想
    假设节点序号是从1到n。
    假设f[0][i][j]是一个n*n的矩阵，第i行第j列代表从i到j的权值，如果i到j有边，那么其值就为ci,j（边ij的权值）。
    如果没有边，那么其值就为无穷大。

    f[k][i][j]代表（k的取值范围是从1到n），在考虑了从1到k的节点作为中间经过的节点时，从i到j的最短路径的长度。

    比如，f[1][i][j]就代表了，在考虑了1节点作为中间经过的节点时，从i到j的最短路径的长度。
    分析可知，f[1][i][j]的值无非就是两种情况，而现在需要分析的路径也无非两种情况，i=>j，i=>1=>j：
    【1】f[0][i][j]：i=>j这种路径的长度，小于，i=>1=>j这种路径的长度
    【2】f[0][i][1]+f[0][1][j]：i=>1=>j这种路径的长度，小于，i=>j这种路径的长度
    形式化说明如下：
    f[k][i][j]可以从两种情况转移而来：
    【1】从f[k−1][i][j]转移而来，表示i到j的最短路径不经过k这个节点
    【2】从f[k−1][i][k]+f[k−1][k][j]转移而来，表示i到j的最短路径经过k这个节点

    总结就是：f[k][i][j]=min(f[k−1][i][j],f[k−1][i][k]+f[k−1][k][j])
    从总结上来看，发现f[k]只可能与f[k−1]有关。
    */

    static final int N = 210,INF = 9999;
    static int n,m,k;
    static int[][] adjacencyMatrix = new int[N][N];
    static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    static int nextInt() throws Exception{
        in.nextToken();
        return (int)in.nval;
    }
    static String next()throws Exception{
        in.nextToken();
        return in.sval;
    }

    static void floyd(){
        for(int k = 1; k <=n; k++) {
          for(int i = 1; i <=n; i++) {
              for(int j = 1; j <=n; j++) {
                  adjacencyMatrix[i][j] = Math.min(adjacencyMatrix[i][j],adjacencyMatrix[i][k]+adjacencyMatrix[k][j]);
              }
          }
        }
    }

    public static void main(String[] args) throws Exception {
        n = nextInt();
        m = nextInt();
        k = nextInt();
        for(int i = 1; i <=n; i++) {
            for(int j = 1; j <=n; j++) {
                if (i == j) {
                    adjacencyMatrix[i][j] = 0;
                }else {
                    adjacencyMatrix[i][j] = INF;
                }
            }
        }
        while (m-- > 0) {
            int a = nextInt();
            int b = nextInt();
            int c =nextInt();
            adjacencyMatrix[a][b] = Math.min(adjacencyMatrix[a][b],c);
            adjacencyMatrix[b][a] = adjacencyMatrix[a][b];
//--------------------无向图----------------------------------
//            adjacencyMatrix[a][b] = adjacencyMatrix[b][a];
//-----------------------------------------------------------
        }
        //        打印邻接矩阵
//        for(int i = 1; i <=n; i++) {
//            for(int j = 1; j <=n; j++) {
//                System.out.printf("%7d",adjacencyMatrix[i][j]);
//            }
//            System.out.println();
//        }
//        System.out.println("------------------------------------");
        floyd();
        while (k-- > 0) {
            int x = nextInt(),y = nextInt();
            if (adjacencyMatrix[x][y]>INF/2){
                System.out.println("impossible");
            }else {
                System.out.println(adjacencyMatrix[x][y]);
            }
        }
//        打印邻接矩阵
//        for(int i = 1; i <=n; i++) {
//            for(int j = 1; j <=n; j++) {
//                System.out.printf("%7d",adjacencyMatrix[i][j]);
//            }
//            System.out.println();
//        }

    }

}

Floyd算法代码(c++)

#include <iostream>
using namespace std;

const int N = 210, M = 2e+10, INF = 1e9;

int n, m, k, x, y, z;
int d[N][N];

void floyd() {
    for(int k = 1; k <= n; k++)
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main() {
    cin >> n >> m >> k;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= n; j++)
            if(i == j) d[i][j] = 0;
            else d[i][j] = INF;
    while(m--) {
        cin >> x >> y >> z;
        d[x][y] = min(d[x][y], z);
        //注意保存最小的边
    }
    floyd();
    while(k--) {
        cin >> x >> y;
        if(d[x][y] > INF/2) puts("impossible");
        //由于有负权边存在所以约大过INF/2也很合理
        else cout << d[x][y] << endl;
    }
    return 0;
}

完整程序

刷题不迷路，欢迎关注博主的git题集，这里有最详细的分类，最经典的例题和最全面的注释

感兴趣的同学可以赏个star吗：算法刷题集git地址 题目源码地址