Logistic Regression 原理及推导 python实现
Posted Maggie张张
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Logistic Regression 原理及推导 python实现相关的知识，希望对你有一定的参考价值。
一、问题引入
首先，Logistic回归是一种广义的线性回归模型，主要用于解决二分类问题。比如，现在我们有N个样本点，每个样本点有两维特征x1和x2，在直角坐标系中画出这N个样本的散点图如下图所示，
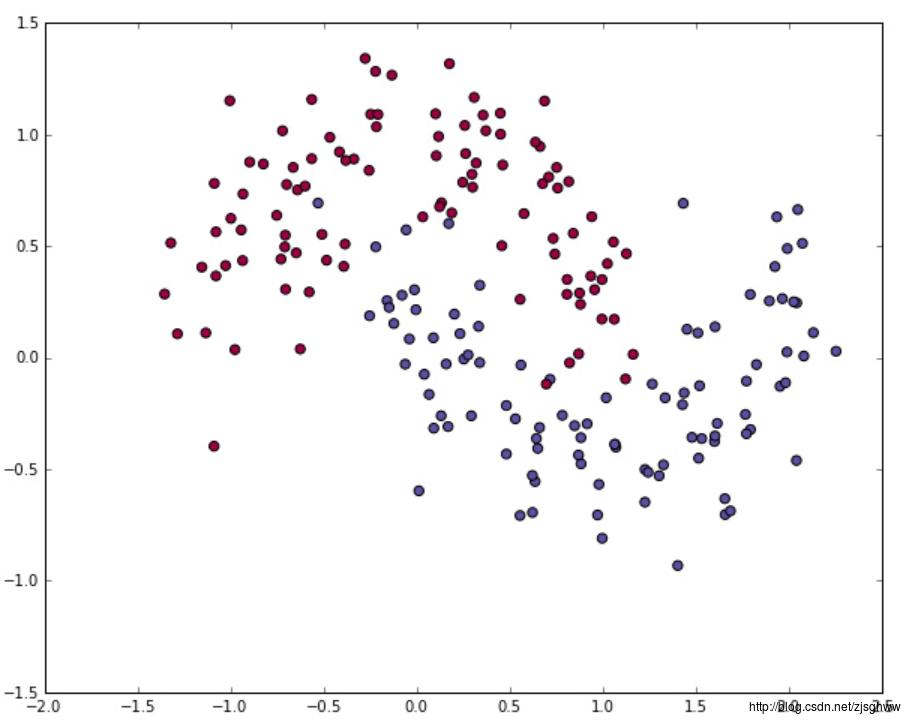
蓝色和红色分别代表两类样本。现在我们的目标是，根据这N个样本所表现出的特征以及他们各自对应的标签，拟合出一条直线对两类样本进行分类，直线的上侧属于第一类，直线的下侧属于第二类。那么我们如何寻找这条直线呢？我们知道，二维空间的一条直线可以用简单的公式表示
y
=
b
+
θ
1
x
1
+
θ
2
x
2
=
θ
T
x
+
b
y= b+\\theta_{1}x_{1}+\\theta_{2}x_{2}= \\theta ^{T}x+b
y=b+θ1x1+θ2x2=θTx+b
参数
θ
T
\\theta^{T}
θT和
b
b
b的选择决定了直线的位置，如果我们选取了一组参数
θ
\\theta
θ和
b
b
b导致直线的位置是这样的
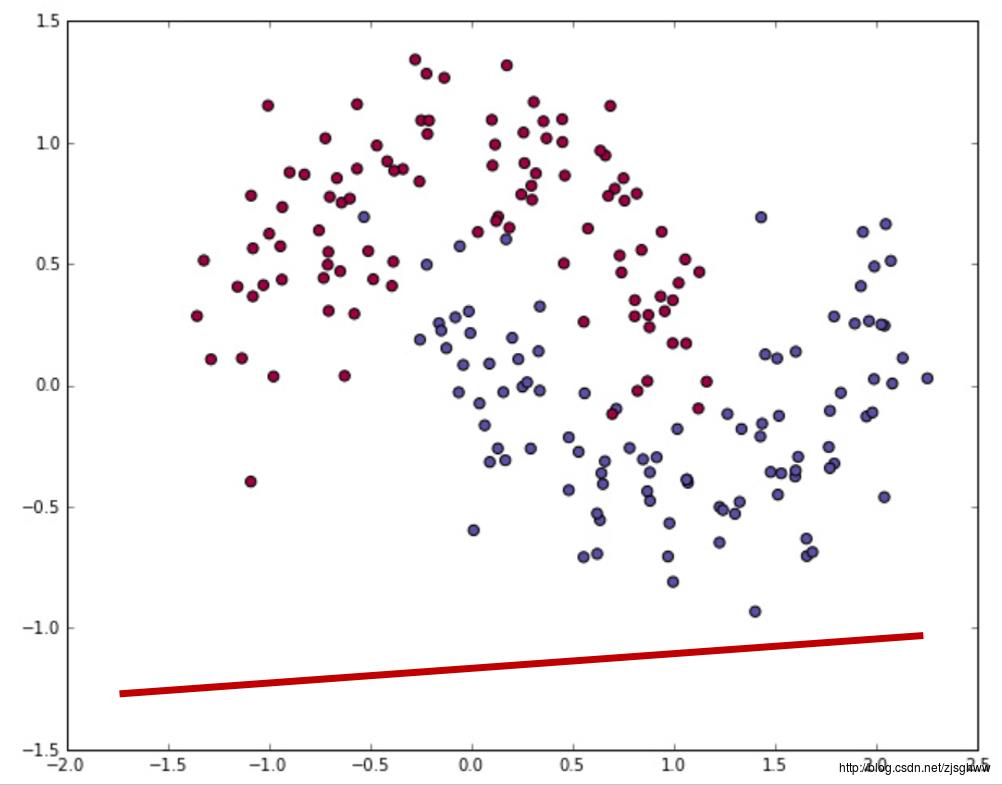
那肯定不合理，因为两类样本完全没有被分开，而如果我们得到了这样一条直线
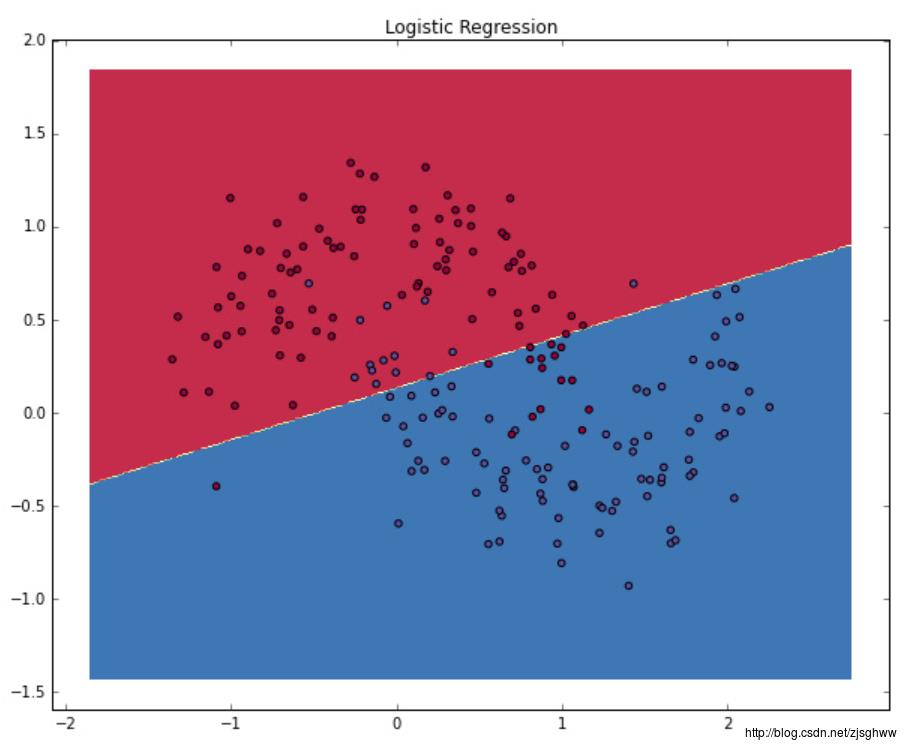
两类样本虽然存在一些小错误，但是基本上被分开了，所以决定这条直线位置的参数和
θ
\\theta
θ 和
b
b
b就是我们想要的答案。由此，我们可以看到，Logistic Regression问题最终变成了求解参数
θ
\\theta
θ的问题。
二、原理
总的来说，Logistic回归的过程就是根据样本求解分类直线（或者超平面）的参数的过程，求解的方法是极大似然估计法，但是因为似然方程最后求导无法得到解析解，所以用了梯度下降法去逐步优化得到极值。
为什么要用极大似然估计法来求解参数呢？
首先，假设样本有k维特征，
x
=
{
x
1
,
x
2
,
.
.
.
,
x
k
}
x=\\left \\{ x_{1},x_{2},...,x_{k} \\right \\}
x={x1,x2,...,xk},
y
∈
{
0
,
1
}
y\\in \\left \\{ 0,1 \\right \\}
y∈{0,1}，用极大似然估计就是在求解怎样的
θ
\\theta
θ 和
b
b
b可以使得出现了某个x时，出现对应的y的概率最大。
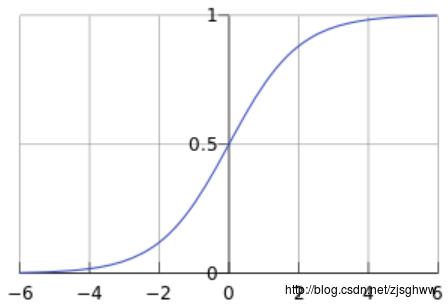
然后，假设这个概率服从的是Sigmoid分布（如下图所示）。样本的每一维特征的取值在经过参数
θ
\\theta
θ线性组合之后取值范围是实数集（-inf, inf），通过Sigmoid变换取值变成了（0，1）。
Sigmoid函数：
g
(
z
)
=
1
1
+
e
−
z
g(z)=\\frac{1}{1+e^{-z}}
g(z)=1+e−z1
三、极大似然估计求解迭代方程
首先，把问题变成一个概率问题：
在某个
x
x
x和
θ
\\theta
θ的取值下，
y
=
1
y=1
y=1的概率为
h
θ
(
x
)
h_{\\theta }(x)
hθ(x)，
P
(
y
=
1
∣
x
;
θ
)
=
h
θ
(
x
)
P(y=1|x;\\theta )=h_{\\theta }(x)
P(y=1∣x;θ)=hθ(x)
在某个
x
x
x和
θ
\\theta
θ的取值下，
y
=
0
y=0
y=0的概率为
1
−
h
θ
(
x
)
1-h_{\\theta }(x)
1−hθ(x)，
P
(
y
=
0
∣
x
;
θ
)
=
1
−
h
θ
(
x
)
P(y=0|x;\\theta )=1-h_{\\theta }(x)
P(y=0∣x;θ)=1−hθ(x)
由于
y
y
y只有两种取值：0和1，因此综合两种情况，对于每一个样本点来说，
P
(
y
∣
x
;
θ
)
=
(
h
θ
(
x
)
)
y
(
1
−
h
θ
(
x
)
)
1
−
y
P(y|x;\\theta )=(h_{\\theta }(x))^{y}(1-h_{\\theta }(x))^{1-y}
P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y
考虑样本集中的所有样本点，由于每个样本之间相互独立，因此它们的联合分布等于各自边际分布之积，
L
(
θ
)
=
∐
i
=
1
m
P
(
y
i
∣
x
i
;
θ
)
=
(
h
θ
(
x
i
)
)
y
i
(
1
−
h
θ
(
x
i
)
)
1
−
y
i
L(\\theta )=\\coprod_{i=1}^{m}P(y_{i}|x_{i};\\theta )=(h_{\\theta }(x_{i}))^{y_{i}}(1-h_{\\theta }(x_{i}))^{1-y_{i}}
L(θ)=i=1∐mP(yi∣xi;θ)=(hθ(xi))yi(1−hθ(xi))1−yi
这就是我们求解 θ \\theta θ需要的似然函数，我们通过他来求解在 θ \\theta θ为何值时， x x x取某个值出现某个 y y y的概率最大。
对 L ( θ ) 取 对 数 L(\\theta)取对数 L(θ)取对数，因为 l n ( x ) ln(x) ln(x)和 x x x单调性相同
l ( θ ) = l n L ( θ ) = ∑ i = 1 m ( y i l n h θ ( x i ) + ( 1 − y i ) l n ( 1 − h θ ( x i ) ) ) l(\\theta )=lnL(\\theta )=\\sum_{i=1}^{m}(y_{i}lnh_{\\theta }(x_{i})+(1-y_{i})ln(1-h_{\\theta }(x_{i}))) l(θ)=lnL(θ)=i=1∑m(yilnhθ(xi)+(1−yi)ln(1−hθ(xi)))
给出损失函数 J ( θ ) = − 1 m l ( θ ) J(\\theta)=-\\frac{1}{m}l(\\theta) J(θ)=−m1l(θ)，对 J ( θ ) J(\\theta) J(θ)求偏导，
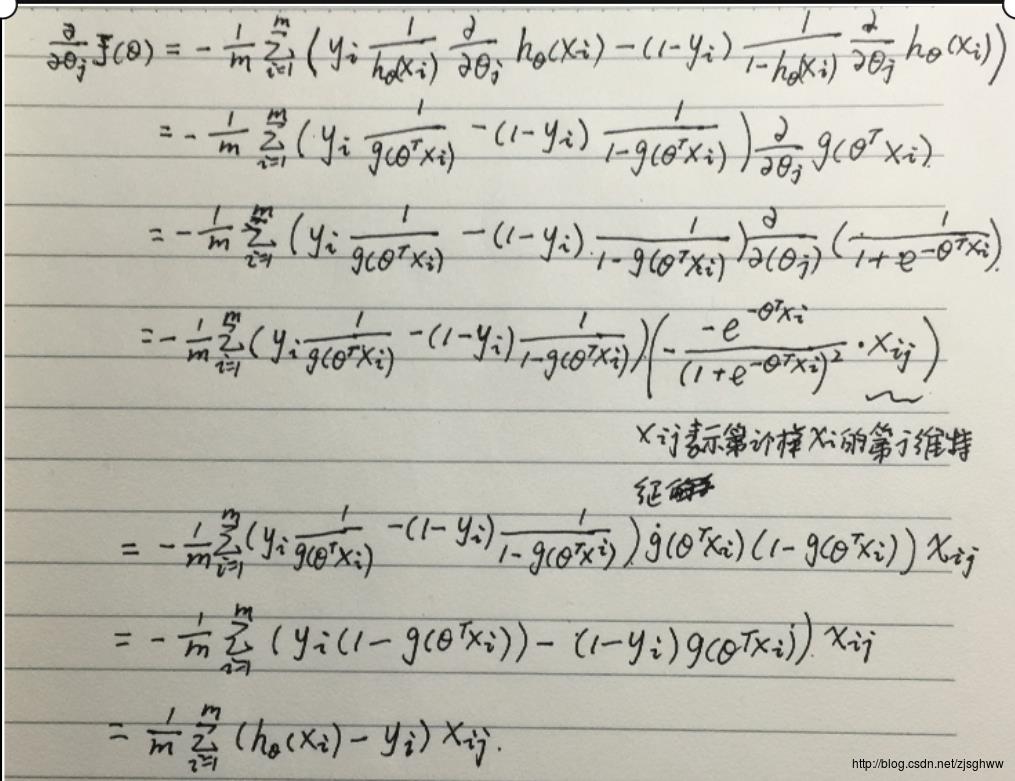
理应令求偏导后的表达式等于零求极值，但是无法解析求解，因此用梯度下降法逐渐迭代，找到局部最优解。
四、梯度下降法求解局部极值
为什么梯度下降法能够做到呢？
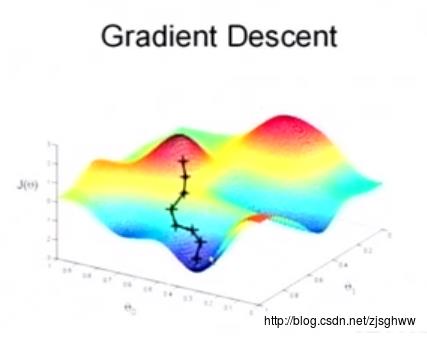
可以看到 θ \\theta θ的取值和 J ( θ ) J(\\theta) J(θ)存在着一一对应的关系，让 θ \\theta 逻辑回归模型 Logistic Regression 详细推导 (含 Numpy 与PyTorch 实现)