N数码问题的启发式搜索算法--A*算法python实现

Posted 2021-01-08 J.mg

• 一、启发式搜索：A算法

1）评价函数的一般形式 : f(n) = g(n) + h(n)

g(n):从S0到Sn的实际代价(搜索的横向因子)

h(n):从N到目标节点的估计代价,称为启发函数(搜索的纵向因子);

特点: 效率高, 无回溯,  

搜索算法

OPEN表 : 存放待扩展的节点.

CLOSED表 : 存放已被扩展过的节点.

2）评价函数  f(x) = g(x) + h(x)   

当f(x) = g(x)   时，为宽度优先搜索

当f(x) = 1/g(x)时，为深度优先搜索

当f(x) = h(x)   时，为全局优先搜索

比较f(x)大小，决定节点搜索顺序，即在OPEN表中的顺序

3)Step1:   把初始节点S0放入OPEN表中;

Step2:   若OPEN表为空,则搜索失败,退出.

Step3:   移出OPEN中第一个节点N放入CLOSED表中, 并标以顺序号n;

Step4:   若目标节点Sg=N, 则搜索成功,结束.

Step5:   若N不可扩展, 则转Step2;

Step6:   扩展N, 生成一组子节点, 对这组子节点作如下处理后, 放入  OPEN表, 按f值重新排序OPEN表, 转 Step2;

删除重复节点和修改返回指针处理.

• 二、启发式搜索：A*算法

1）评价函数的一般形式:

f(n) = g(n) + h(n)  且  h(n) <= h*(n)

g(n),h(n):定义同A算法;

h*(n):从N到目标节点的最短路径; 称此时的A算法为A*算法.

2）程序关键点

节点的扩展：close表存放已经扩展后的状态，open表存放未扩展的状态。首先获取节点能扩展的方向，扩展后将父节点放入close表中，如果转移之后的节点，既不在close表也不再open表，表明该节点还未被扩展，则插入open表，如果在close表中表明之前已经扩展过该状态，为了避免无限扩展应将该状态从open表舍弃，如果在open表则比较这两个矩阵的f值（选取最优解），留小的在open表，之后对open表中的节点根据f值进行排序，pop出f值最小的节点进行扩展，依次进行该过程，直至该节点为目标状态。
解的路径的输出：通过目标状态节点向上回溯找其父节点，直至开始状态。

 

• 三、python代码实现

  1 # -*- coding: utf-8 -*-
  2 """
  3 Created on Sun Sep 16 14:31:40 2018
  4 A*算法解决N数码问题
  5 运行程序后如下是输入格式:
  6         请输入矩阵的行数
  7         
  8         3                            输入对应的N
  9         请输入初始矩阵A               
 10         
 11         1 0 2                        一行行输入，每行数字空格隔开，每行最后一个数字输入完成后直接回车开始输入第二行
 12         
 13         4 5 6
 14         
 15         3 7 8
 16         请输入目标矩阵B
 17         
 18         1 2 3
 19         
 20         8 0 4
 21         
 22         7 6 5
 23     
 24 """
 25 import numpy as np
 26 import copy
 27 import time
 28 from operator import itemgetter
 29 
 30 goal = {}
 31 
 32 def get_location(vec, num):    #根据num元素获取num在矩阵中的位置
 33     row_num = vec.shape[0]     #numpy-shape函数获得矩阵的维数
 34     line_num = vec.shape[1]
 35     
 36     for i in range(row_num):
 37         for j in range(line_num):
 38             if num == vec[i][j]:
 39                 return i, j
 40 
 41 def get_actions(vec):    #获取当前位置可以移动的下一个位置，返回移动列表
 42     row_num = vec.shape[0]
 43     line_num = vec.shape[1]
 44     
 45     (x, y) = get_location(vec, 0)    #获取0元素的位置
 46     action = [(0, 1), (0, -1), (1, 0), (-1, 0)]
 47     
 48     if x == 0:    #如果0在边缘则依据位置情况，减少0的可移动位置
 49         action.remove((-1, 0))
 50     if y == 0:
 51         action.remove((0, -1))
 52     if x == row_num - 1:
 53         action.remove((1, 0))
 54     if y == line_num - 1:
 55         action.remove((0, 1))
 56         
 57     return list(action)
 58 
 59 def result(vec, action):    #移动元素，进行矩阵转化
 60      (x, y) = get_location(vec, 0)    #获取0元素的位置
 61      (a, b) = action    #获取可移动位置
 62                                  
 63      n = vec[x+a][y+b]    #位置移动，交换元素
 64      s = copy.deepcopy(vec)
 65      s[x+a][y+b] = 0
 66      s[x][y] = n
 67      
 68      return s
 69     
 70 def get_ManhattanDis(vec1, vec2):    #计算两个矩阵的曼哈顿距离,vec1为目标矩阵,vec2为当前矩阵
 71     row_num = vec1.shape[0]
 72     line_num = vec1.shape[1]
 73     dis  = 0
 74     
 75     for i in range(row_num):
 76         for j in range(line_num):
 77             if vec1[i][j] != vec2[i][j] and vec2[i][j] != 0:
 78                 k, m = get_location(vec1, vec2[i][j])
 79                 d = abs(i - k) + abs(j - m)
 80                 dis += d
 81                 
 82     return dis
 83 
 84 def expand(p, actions, step):                          #actions为当前矩阵的可扩展状态列表,p为当前矩阵,step为已走的步数
 85     children = []                                      #children用来保存当前状态的扩展节点
 86     for action in actions:
 87         child = {}
 88         child[\'parent\'] = p
 89         child[\'vec\'] = (result(p[\'vec\'], action))
 90         child[\'dis\'] = get_ManhattanDis(goal[\'vec\'], child[\'vec\'])
 91         child[\'step\'] = step + 1                       #每扩展一次当前已走距离加1
 92         child[\'dis\'] = child[\'dis\'] + child[\'step\']    #更新该节点的f值  f=g+h（step+child[dis]）                     
 93         child[\'action\'] = get_actions(child[\'vec\'])
 94         children.append(child)
 95     
 96     return children
 97 
 98 def node_sort(nodelist):    #按照节点中字典的距离字段对列表进行排序,从大到小
 99     return sorted(nodelist, key = itemgetter(\'dis\'), reverse=True)
100 
101 def get_input(num):
102     A = []
103     for i in range(num):
104         temp = []
105         p = []
106         s = input()
107         temp = s.split(\' \')
108         for t in temp:
109             t = int(t)
110             p.append(t)
111         A.append(p)
112    
113     return A  
114 
115 def get_parent(node):
116     q = {}
117     q = node[\'parent\']   
118     return q
119         
120 def test():
121     openlist = []    #open表
122     close = []       #存储扩展的父节点
123     
124     print(\'请输入矩阵的行数\')
125     num = int(input())  
126     
127     print("请输入初始矩阵A")
128     A = get_input(num)
129  
130     print("请输入目标矩阵B")
131     B = get_input(num)
132     
133     print("请输入结果文件名")
134     resultfile = input()
135     
136     goal[\'vec\'] = np.array(B)   #建立矩阵
137    
138     p = {}
139     p[\'vec\'] = np.array(A)
140     p[\'dis\'] = get_ManhattanDis(goal[\'vec\'], p[\'vec\'])
141     p[\'step\'] = 0
142     p[\'action\'] = get_actions(p[\'vec\'])
143     p[\'parent\'] = {}
144 
145     if (p[\'vec\'] == goal[\'vec\']).all():
146         return
147     
148     openlist.append(p)
149     
150     start_CPU = time.clock()    #开始扩展时CPU开始计算
151     
152     while openlist:
153         
154         children = []
155         
156         node = openlist.pop()    #node为字典类型，pop出open表的最后一个元素
157         close.append(node)  #将该元素放入close表
158       
159         if (node[\'vec\'] == goal[\'vec\']).all():    #比较当前矩阵和目标矩阵是否相同
160             end_CPU = time.clock()    #CPU结束计算
161          
162             h = open(resultfile,\'w\',encoding=\'utf-8\',)  #将结果写入文件  并在控制台输出
163             h.write(\'搜索树规模：\' + str(len(openlist)+len(close)) + \'\\n\')
164             h.write(\'close：\' + str(len(close)) + \'\\n\')
165             h.write(\'openlist：\' + str(len(openlist)) + \'\\n\')
166             h.write(\'cpu运行时间：\' + str(end_CPU - start_CPU) + \'\\n\')
167             h.write(\'路径长：\' + str(node[\'dis\']) + \'\\n\')
168             
169             h.write(\'解的路径：\' + \'\\n\')
170             i = 0
171             way = []
172             while close:
173                 way.append(node[\'vec\'])  #从最终状态开始依次向上回溯将其父节点存入way列表中
174                 node = get_parent(node)
175                 if(node[\'vec\'] == p[\'vec\']).all():
176                     way.append(node[\'vec\'])
177                     break
178             while way:
179                 i += 1
180                 h.write(str(i) + \'\\n\')
181                 h.write(str(way.pop()) + \'\\n\')
182             h.close()
183             f = open(resultfile,\'r\',encoding=\'utf-8\',)
184             print(f.read())
185             
186             return
187         
188         children = expand(node, node[\'action\'], node[\'step\'])    #如果不是目标矩阵，对当前节点进行扩展，取矩阵的可能转移情况
189         
190         for child in children:     #如果转移之后的节点，既不在close表也不再open表则插入open表，如果在close表中则舍弃，如果在open表则比较这两个矩阵的f值，留小的在open表
191             f = False
192             flag = False
193             j = 0
194             for i in range(len(openlist)):
195                 if (child[\'vec\'] == openlist[i][\'vec\']).all():
196                     j = i
197                     flag = True
198                     break
199             for i in range(len(close)):
200                 if(child[\'vec\'] == close[i]).all():
201                     f = True
202                     break
203             if  f == False and flag == False :
204                 openlist.append(child)
205                 
206             elif flag == True:
207                 if child[\'dis\'] < openlist[j][\'dis\']:
208                     del openlist[j]
209                     openlist.append(child)
210                     
211         
212         openlist = node_sort(openlist)   #对open表进行从大到小排序
213     
214 test()

 

• 四、程序运行结果如下图所示

 

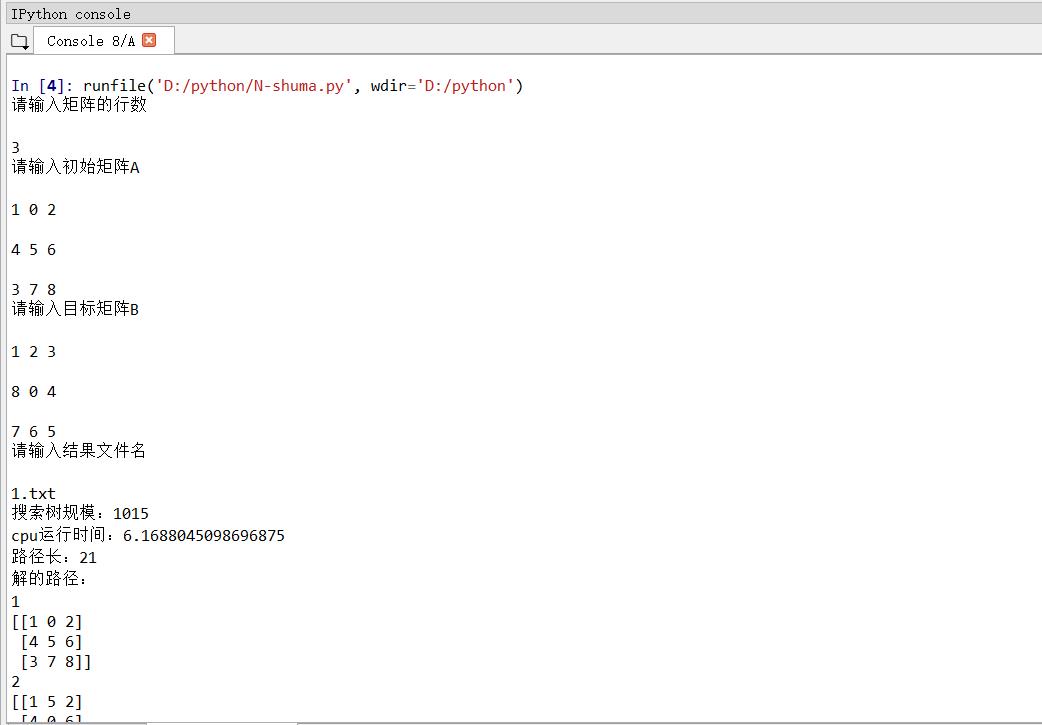
                                                             图 1

 

                                                            图 2

 

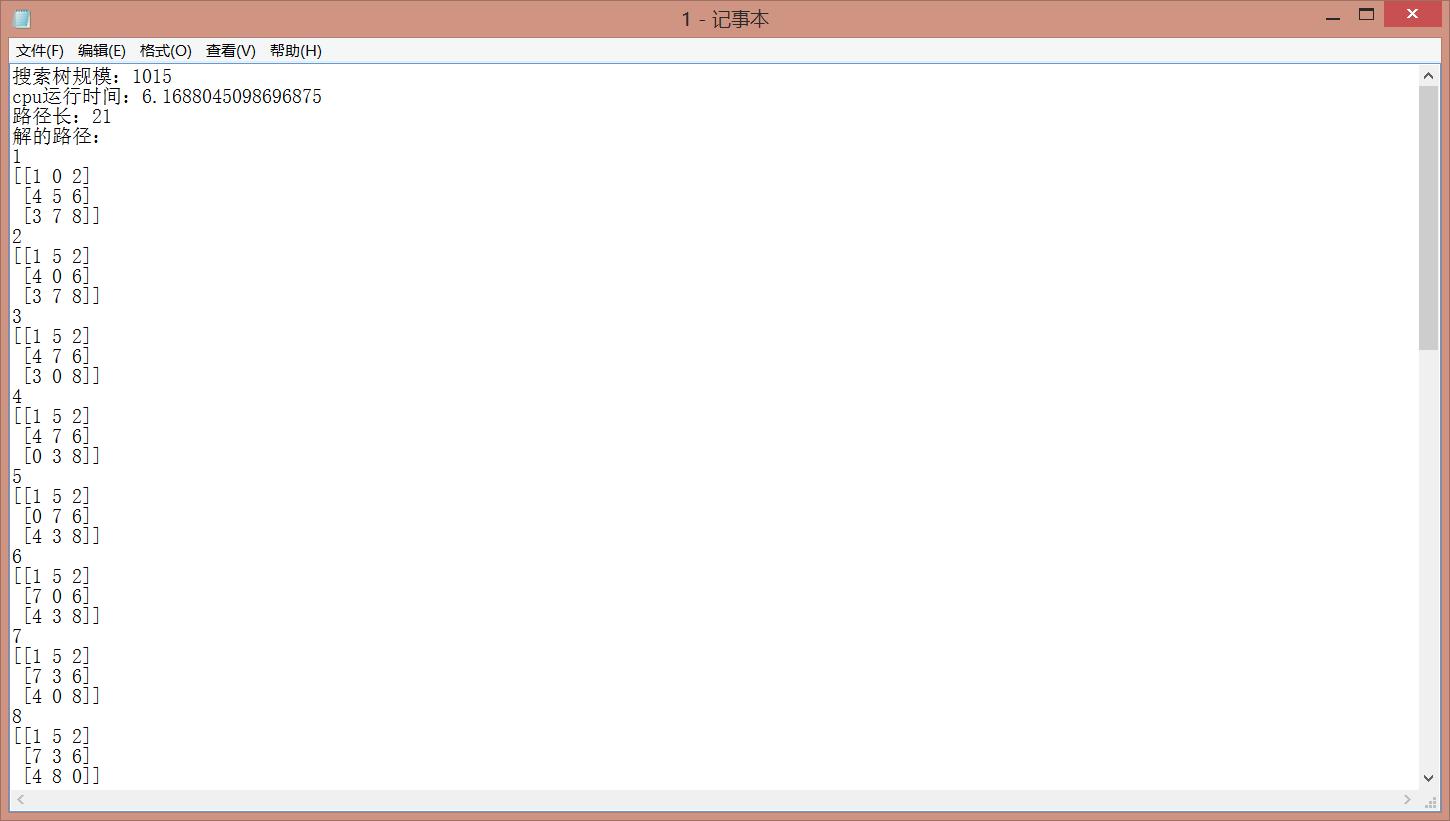
                                                                图 3

• 五、总结

通过这次编程了解到了搜索具有探索性，要提高搜索效率(尽快地找到目标节点)，或要找最佳路径(最佳解)就必须注意搜索策略。对于状态图搜索，已经提出了许多策略，它们大体可分为盲目搜索（bland search)和启发式搜索（heuristic search）两大类。其中盲目搜索是无向导搜索。启发式搜索是有向导搜索，即利用启发信息（函数）引导去寻找问题解。通过A*算法解决N数码问题实验过程中也遇到很多问题，比如节点扩展的方向问题等，通过这次实验不仅锻炼了自己python编程能力，也让自己对N数码求解最优路径问题有了更清晰的认识，希望自己能在老师和同学的帮助下，能不断进步，当然最重要的是自己得付出，只会幻想而不行动的人,永远也体会不到收获果实时的喜悦。加油！！