中心极限定理的最最通俗解释

Posted 2023-05-11

参考技术A 在适当的条件下，大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。每次从这些总体中随机抽取 n 个抽样，一共抽 m 次。 然后把这 m 组抽样分别求出平均值， 这些平均值的分布接近正态分布。设从均值为μ、方差为 （有限）的任意一个总体中抽取样本量为n的样本，当n充分大时，样本均值 的抽样分布近似服从均值为μ、方差为 的正态分布。

中心极限定理告诉我们，当样本量足够大时，样本均值的分布慢慢变成正态分布，就像下图：

下面我们来通过实例来看看一个掷骰子的平均分布，如何组成一个正态分布。

生成在半开半闭区间[low,high)上离散均匀分布的整数值，即1-6的均匀分布

可以看到1-6的点数是比较均匀的分布的【注意，每一次运行的图都不一样的哦】

通过以下程序来从data中随机抽取一组数

返回结果：[2, 3, 2, 1, 1, 4, 2, 1, 5, 3]

我们在生产的随机数中，一次抽取50个作为一组并计算它的平均值，共抽取1000次，得到1000个平均值，然后通过seaborn的distplot看着1000个数值的分布。

当采样的数量接近无穷大时，我们的抽样分布就会近似于正态分布。这个统计学基础理论意味着我们能根据个体样本推断所有样本。结合正态分布的其他知识，我们可以轻松计算出给定平均值的值的概率。在理论上保证了我们可以用只抽样一部分的方法，达到推测研究对象统计参数的目的。

其中要注意的几点：

中心极限定理

中心极限定理指的是给定一个任意分布的总体。每次从这些总体中随机抽取 n 个抽样，一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。

我们先举个栗子
现在我们要统计全国的人的体重，看看我国平均体重是多少。当然，我们把全国所有人的体重都调查一遍是不现实的。所以我们打算一共调查1000组，每组50个人。 然后，我们求出第一组的体重平均值、第二组的体重平均值，一直到最后一组的体重平均值。中心极限定理说：这些平均值是呈现正态分布的。并且，随着组数的增加，效果会越好。 最后，当我们再把1000组算出来的平均值加起来取个平均值，这个平均值会接近全国平均体重。

其中要注意的几点：

1.总体本身的分布不要求正态分布
上面的例子中，人的体重是正态分布的。但如果我们的例子是掷一个骰子（平均分布），最后每组的平均值也会组成一个正态分布。（神奇！）

2.样本每组要足够大，但也不需要太大
取样本的时候，一般认为，每组大于等于30个，即可让中心极限定理发挥作用。

话不多说，我们现在来一步步看到中心极限定理是如何起作用的。

第一步， 生成数据
假设我们现在观测一个人掷骰子。这个骰子是公平的，也就是说掷出1~6的概率都是相同的：1/6。他掷了一万次。我们用python来模拟投掷的结果：

 

 

平均值接近3.5很好理解。 因为每次掷出来的结果是1、2、3、4、5、6。 每个结果的概率是1/6。所以加权平均值就是3.5。

第二步，画出来看看
我们把生成的数据用直方图画出来直观地感受一下：

 

 

 

 

 

 

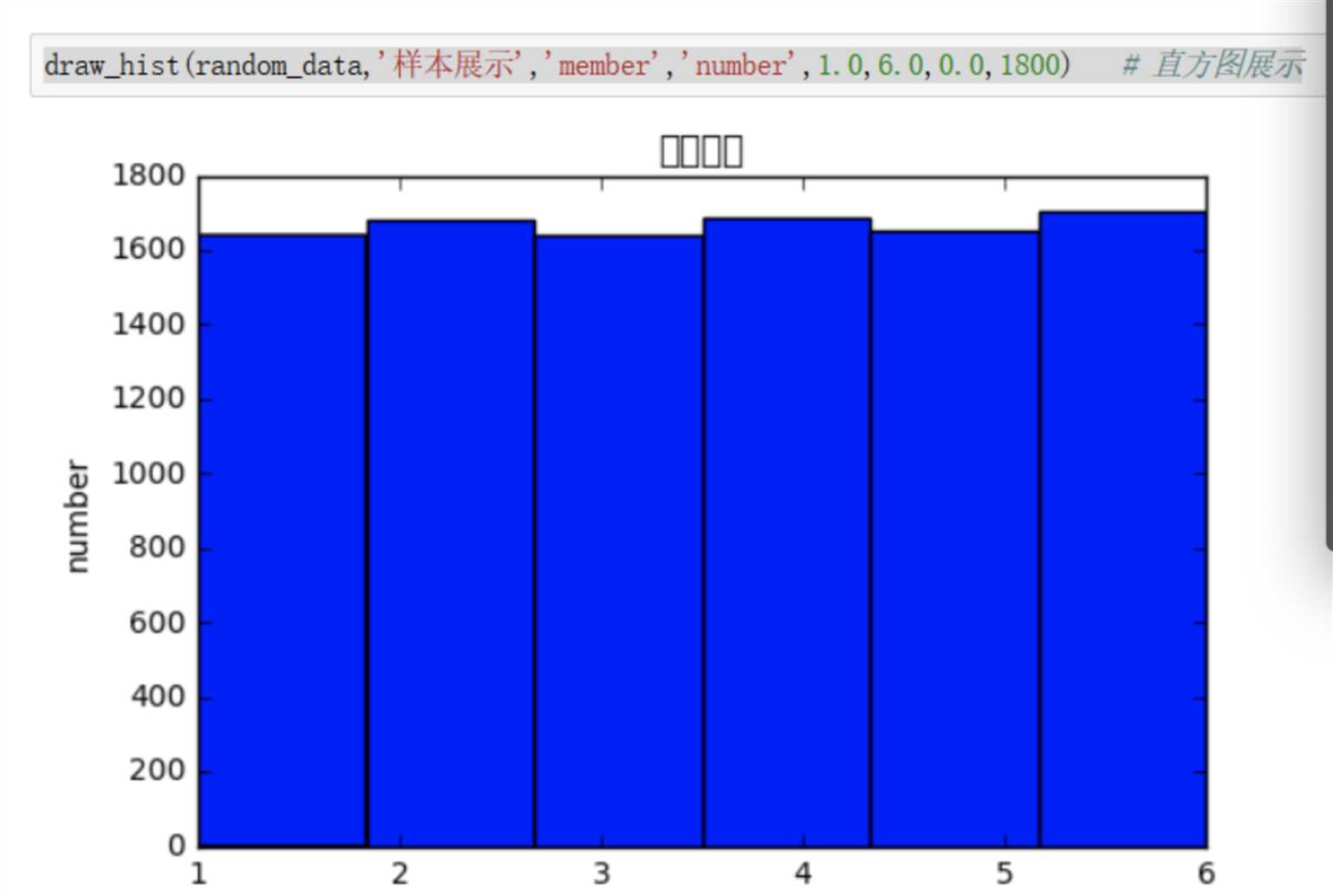
可以看到1~6分布都比较平均，不错。

第三步，抽一组抽样来试试
我们接下来随便先拿一组抽样，手动算一下。例如我们先从生成的数据中随机抽取10个数字：

 

 

平均值：3.9
标准差：1.51
可以看到，我们只抽10个的时候，样本的平均值（3.9）会距离总体的平均值（3.5）有所偏差。
有时候我们运气不好，抽出来的数字可能偏差很大，比如抽出来10个数字都是6。那平均值就是6了。 为什么会出现都是6的情况呢？因为这就是随机的魅力呀！
不过不要担心，接下去就是见证奇迹的时刻。
第四步，见证奇迹的时刻
我们让中心极限定理发挥作用。现在我们抽取1000组，每组50个。
我们把每组的平均值都算出来。

 

 

 

 

我们把这1000个数字用直方图画出来：

 

 

 

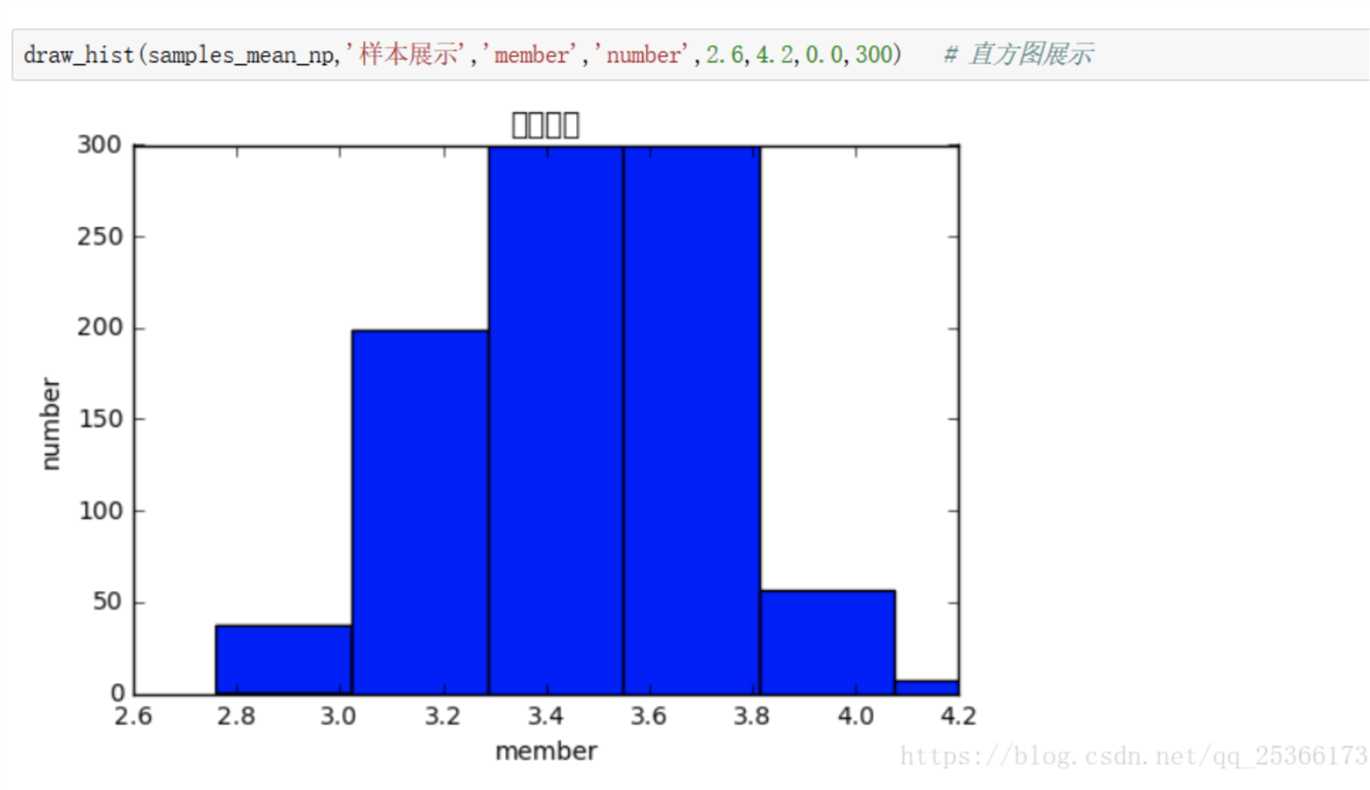
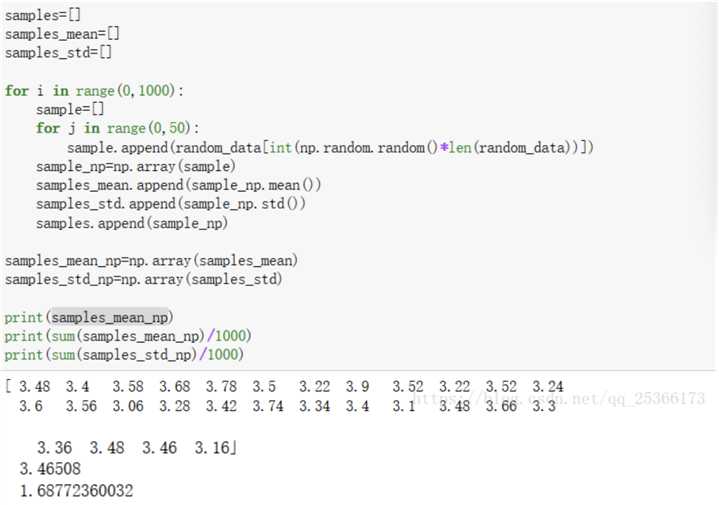
结果打印如下：
平均值：3.46508
标准差：1.68772

在实际生活当中，我们不能知道我们想要研究的对象的平均值，标准差之类的统计参数。中心极限定理在理论上保证了我们可以用只抽样一部分的方法，达到推测研究对象统计参数的目的。
在上文的例子中，掷骰子这一行为的理论平均值3.5是我们通过数学定理计算出来的。而我们在实际模拟中，计算出来的样本平均值的平均值（3.48494）确实已经和理论值非常接近了。