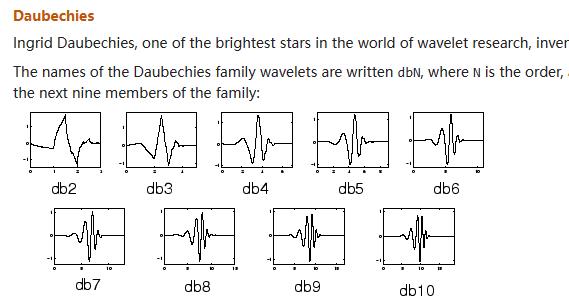
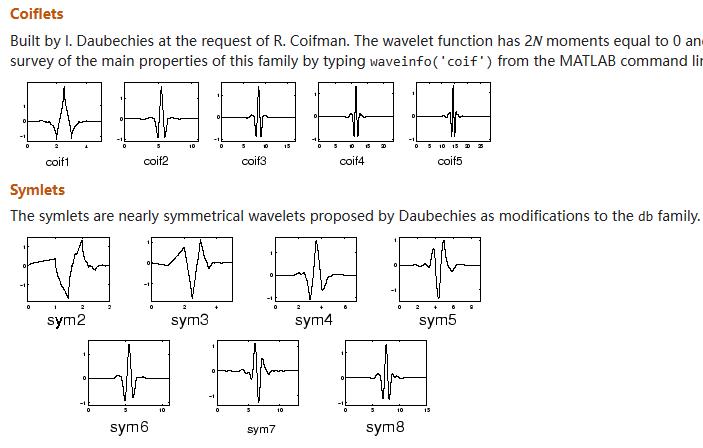
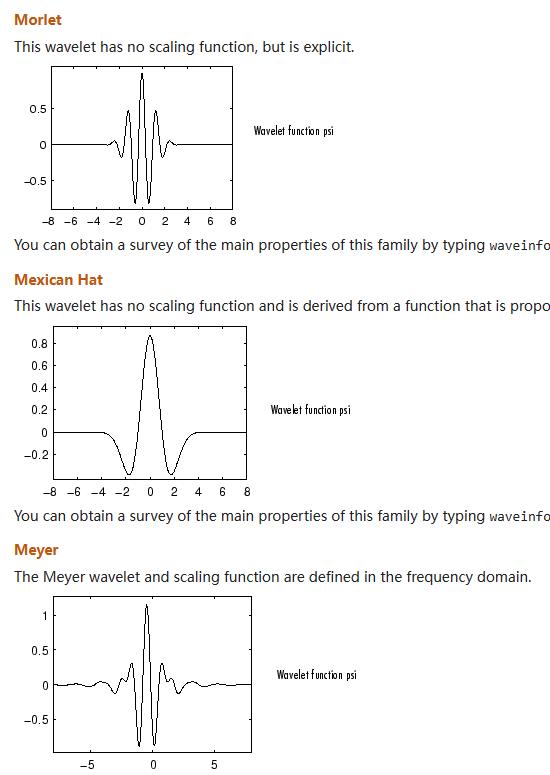
小波家族（Wavelet Families）

Posted 2023-05-10 SusieSnail_SUN

摘自： Introduction to Wavelet Families - MATLAB & Simulink - MathWorks 中国

 

 

 

 

用pyWavelet进行多级部分小波重构

我正在寻找一种方法来部分重建小波分解的分支，以便总和将重建原始信号。这可以使用Matlab实现：

DATA = [0,1,2,3,4,5,6,7,8,9]
N_LEVELS = 2;
WAVELET_NAME = 'db4';
[C,L] = wavedec(DATA, N_LEVELS, WAVELET_NAME);
A2 = wrcoef('a', C, L, WAVELET_NAME, 2);
D2 = wrcoef('d', C, L, WAVELET_NAME, 2);
D1 = wrcoef('d', C, L, WAVELET_NAME, 1);
A2+D2+D1

ans =

    0.0000    1.0000    2.0000    3.0000    4.0000    5.0000    6.0000    7.0000    8.0000    9.0000

我想用pywt实现同样的目标，但我不知道如何解决这个问题。 pywt.waverec函数创建完整重建，但没有用于部分重建的级别参数。 pywt.upcoef函数可以完成单个级别所需的功能，但我不确定如何将其扩展为多个级别：

>>> import pywt
>>> data = [1,2,3,4,5,6]
>>> (cA, cD) = pywt.dwt(data, 'db2', 'smooth')
>>> n = len(data)
>>> pywt.upcoef('a', cA, 'db2', take=n) + pywt.upcoef('d', cD, 'db2', take=n)
array([ 1.,  2.,  3.,  4.,  5.,  6.])

答案

我设法写了我自己的wrcoef函数版本，看起来像预期的那样工作：

import pywt
import numpy as np

def wrcoef(X, coef_type, coeffs, wavename, level):
    N = np.array(X).size
    a, ds = coeffs[0], list(reversed(coeffs[1:]))

    if coef_type =='a':
        return pywt.upcoef('a', a, wavename, level=level)[:N]
    elif coef_type == 'd':
        return pywt.upcoef('d', ds[level-1], wavename, level=level)[:N]
    else:
        raise ValueError("Invalid coefficient type: ".format(coef_type))



level = 4
X = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]
coeffs = pywt.wavedec(X, 'db1', level=level)
A4 = wrcoef(X, 'a', coeffs, 'db1', level)
D4 = wrcoef(X, 'd', coeffs, 'db1', level)
D3 = wrcoef(X, 'd', coeffs, 'db1', 3)
D2 = wrcoef(X, 'd', coeffs, 'db1', 2)
D1 = wrcoef(X, 'd', coeffs, 'db1', 1)
print A4 + D4 + D3 + D2 + D1

# Results:
[  9.99200722e-16   1.00000000e+00   2.00000000e+00   3.00000000e+00
   4.00000000e+00   5.00000000e+00   6.00000000e+00   7.00000000e+00
   8.00000000e+00   9.00000000e+00   1.00000000e+01   1.10000000e+01
   1.20000000e+01   1.30000000e+01   1.40000000e+01   1.50000000e+01
   1.60000000e+01   1.70000000e+01]

另一答案

目前，pywt尚未实现wrcoef等效功能。但您仍然可以分解1-D多电平信号，然后分别重建其组件。

import pywt
def decomposite(signal, coef_type='d', wname='db6', level=9):
    w = pywt.Wavelet(wname)
    a = data
    ca = []
    cd = []
    for i in range(level):
        (a, d) = pywt.dwt(a, w, mode)
        ca.append(a)
        cd.append(d)
    rec_a = []
    rec_d = []
    for i, coeff in enumerate(ca):
        coeff_list = [coeff, None] + [None] * i
        rec_a.append(pywt.waverec(coeff_list, w))
    for i, coeff in enumerate(cd):
        coeff_list = [None, coeff] + [None] * i
        rec_d.append(pywt.waverec(coeff_list, w))
    if coef_type == 'd':
        return rec_d
    return rec_a

我们需要将返回值切片以使输入信号具有相同的长度。然后我们可以在分解后获得每个组件。

X = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]
rec_d = decomposite(X, 'd', 'db6', level=9)
# slice rec_d
print sum(rec_d )