Python 实现快排

Posted 2021-01-05 QQ_990814268

快速排序简介
快速排序，又称划分交换排序，从无序队列中挑取一个元素，把无序队列分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
简单来说：挑元素、划分组、分组重复前两步

快速排序原理示意图
通过上面对快速排序的简介，我们知道了，快速排序主要包括以下两方面：
挑元素划分组、整体递归分组
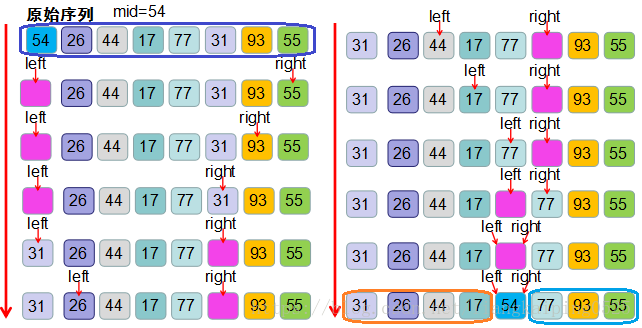
挑元素划分组示意图：

特点：
1、因为是无序队列，所以位置可以随机挑
2、临时划分一个空间，存放我们挑选出来的中间元素
3、左标签位置空，移动右标签，反之一样
4、重复3，直到左右侧标签指向同一个位置，
5、把临时存放的中间元素，归位
一句话：左手右手一个慢动作，右手左手慢动作重播

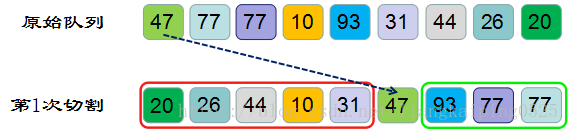
整体划分示意图：

特点：
1、递归拆分
2、拆分到最后，所有小组内的元素个数都是1
一句话：递归拆分到不能再拆

代码实践分析
根据上面两个示意图的分析，我们要从两个大方面分析：
序列切割 和 递归拆分

1、序列切割
序列切割这个知识点，我们从四个方面分别介绍：
3个基本标签、右侧推进、左侧推进、停止推进(即元素归位)

1.1、3个基本标签
大小区域切割，至少涉及到三个标签：
mid：指定要切割的临时中间数字    
left：从队列左侧推进的标签
right：从队列右侧推进的标签                                     

 1 def quick_sort(li, start, end):
 2     # 分治 一分为二
 3     # start=end ,证明要处理的数据只有一个
 4     # start>end ,证明右边没有数据
 5     if start >= end:
 6         return
 7     # 定义两个游标，分别指向0和末尾位置
 8     left = start
 9     right = end
10     # 把0位置的数据，认为是中间值
11     mid = li[left]
12     while left < right:
13         # 让右边游标往左移动，目的是找到小于mid的值，放到left游标位置
14         while left < right and li[right] >= mid:
15             right -= 1
16         li[left] = li[right]
17         # 让左边游标往右移动，目的是找到大于mid的值，放到right游标位置
18         while left < right and li[left] < mid:
19             left += 1
20         li[right] = li[left]
21     # while结束后，把mid放到中间位置，left=right
22     li[left] = mid
23     # 递归处理左边的数据
24     quick_sort(li, start, left-1)
25     # 递归处理右边的数据
26     quick_sort(li, left+1, end)
27  
28 if __name__ == ‘__main__‘:
29     l = [6,5,4,3,2,1]
30     # l = 3 [2,1,5,6,5,4]
31     # [2, 1, 5, 6, 5, 4]
32     quick_sort(l,0,len(l)-1)
33     print(l)
34     # 稳定性：不稳定
35     # 最优时间复杂度：O(nlogn)
36     # 最坏时间复杂度：O(n^2)

 

关键点：
序列切割：
1、挑中间元素：mid = alist[start]
2、右推进：while right > left and alist[right] >= mid:
3、左推进：while left < right and alist[left] < mid:
4、推进循环：while left < right:
5、元素归位：alist[left] = mid
递归拆分：
1、小组边界确定：left = start、right = end
2、递归退出条件：if start < end:
3、函数自调用：quick_sort(alist, start, end)

时间复杂度
最优时间复杂度：O(nlogn)
对于每次快排，left和right的标签分别在左右两册数据全部都移动了一遍，相当于遍历了所有数据，那么时间复杂度是O(n)
因为涉及到了递归分组，所以他的时间复杂度是O(logn)
整体来说：最优的时间复杂度是 O(nlogn)

最坏时间复杂度：O(n2)

因为递归分组分组的条件不一定是二分，有可能每一次mid指定的都是最大或者最小，那么有多少个元素，我们就可能分多少次组，这种情况时间复杂度就是O(n)了
所以最坏的时间复杂度就是O(n2)，那么最坏也不过如此了。
稳定性：不稳定

思考：
改哪个地方，结果是降序？
while right > left and alist[right] >= mid:     代码中的 >= 改为 <=
while left < right and alist[left] < mid         代码中的 < 改为 >
本节内容小结：
1、快速排序原理：挑元素、划分组，分组重复前两步。
2、快速排序实践步骤：
划分组:准备工作+左右移动+元素归位
递归:函数自调用+退出条件