图像标注 python实现-LSTM篇

Posted 2021-01-03 Super_JJboom

上一篇文章介绍了RNN的工作原理和在图像标注上的应用，这篇介绍RNN的变体LSTM。

要知道为什么会出现LSTM，首先来看RNN存在什么问题。RNN由于激活函数和本身结构的问题，存在梯度消失的现象，导致

（1）网络结构不能太深，不然深层网络的梯度可以基本忽略，没有起到什么作用，白白增加训练时间。

（2）只能形成短期记忆，不能形成长期记忆。 因为梯度逐层减少，只有比较临近的层梯度才会相差不多，所以对临近的信息记忆比较多，对较远的信息记忆差。

接下来看看LSTM怎么解决这个问题：

所有 RNN 都具有一种重复神经网络模块的链式的形式。在标准的 RNN 中，这个重复的模块只有一个非常简单的结构，例如一个 tanh 层。

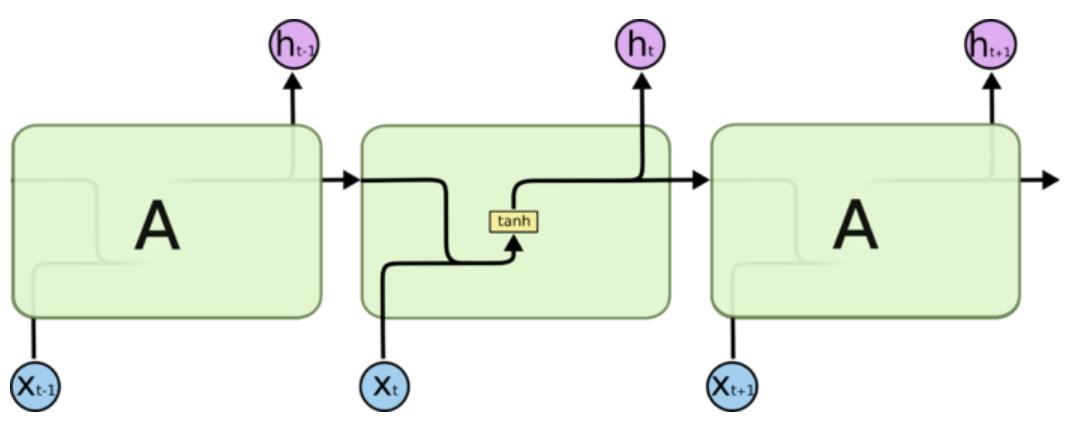
正是由于tanh导数恒小于1，出现的梯度越来越小的问题。

 

LSTM通过更加精细的在每步时间节点的计算克服梯度问题，RNN把一个状态信息用一次计算更新，LSTM用四次计算来更新，即“四个门”。

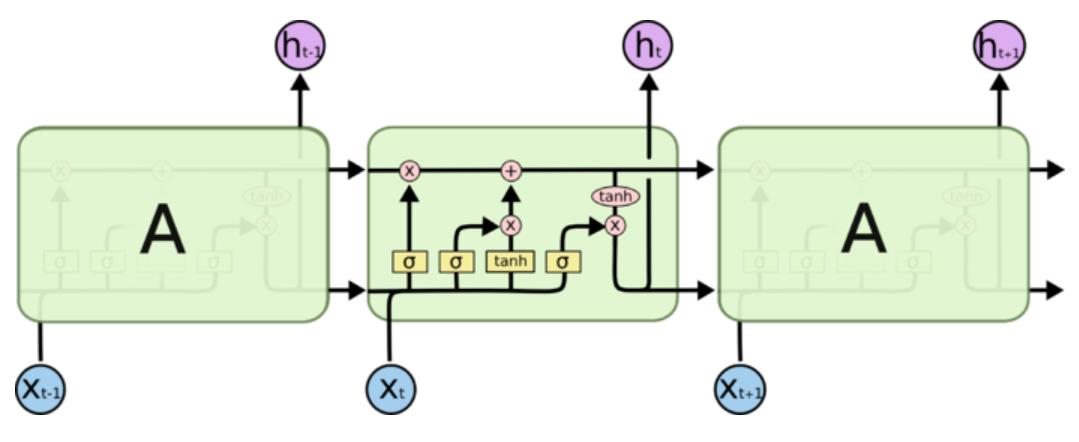
原本我是把h叫做状态的，但是在这个新的结构里，h叫状态已经不太合适了，有一个新的变量C才是真正意义上的状态，好像大部分资料都把C叫做细胞状态，至于h，我现在也不知道怎么称呼它好了，它确实也在传播状态信息，但是却是可有可无的，因为h的值完全可以由C得到，不显式传递也不会有任何问题。

 

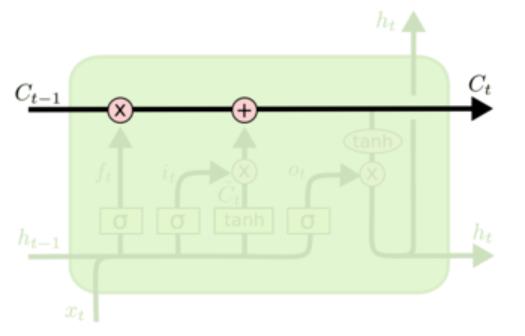
在RNN中，$x_t\\in \\mathbb{R}^{D} ,h_t\\in \\mathbb{R}^H, W_x\\in\\mathbb{R}^{H\\times D}, W_h\\in\\mathbb{R}^{H\\times H},b\\in\\mathbb{R}^{H}$。

在LSTM中，$x_t\\in \\mathbb{R}^{D}, h_t\\in \\mathbb{R}^H, W_x\\in\\mathbb{R}^{4H\\times D}, W_h\\in\\mathbb{R}^{4H\\times H},b\\in\\mathbb{R}^{4H}$。

第一步还是一样，$a\\in\\mathbb{R}^{4H}$ ， $a=W_xx_t + W_hh_{t-1}+b$，RNN得到a直接就可以直接激活当作下一个状态了，而LSTM中得到了四个输出。

$$
\\begin{align*}
i = \\sigma(a_i) \\hspace{2pc}
f = \\sigma(a_f) \\hspace{2pc}
o = \\sigma(a_o) \\hspace{2pc}
g = \\tanh(a_g)
\\end{align*}
$$

i，f，o，g分别叫做输入门，遗忘门，输出门，阻塞门，$i,f,o,g\\in\\mathbb{R}^H$。

$$
c_{t} = f\\odot c_{t-1} + i\\odot g \\hspace{4pc}
h_t = o\\odot\\tanh(c_t)
$$

下面来理解一下这些公式：

“遗忘“可以理解为“之前的内容记住多少“，其精髓在于只能输出（0，1）小数的sigmoid函数和粉色圆圈的乘法，LSTM网络经过学习决定让网络记住以前百分之多少的内容。

下一步是确定什么样的新信息被存放在细胞状态中。这里包含两个部分。第一，sigmoid 层称 “输入门层” 决定什么值我们将要更新。然后，一个 tanh 层称“阻塞门层”创建一个新的候选值向量加入到状态中。下一步，我们会讲这两个信息来产生对状态的更新。

最终，我们需要确定输出什么值。这个输出将会基于我们得到的的新的细胞状态和“输出门”的信息。

有了遗忘门和输入门之后，在对h求导，这时候的导数已经不是恒小于1了，所以克服了梯度消失的问题。（关于RNN和LSTM的梯度可以在代码中很清晰的看到对比，当然也可以手动直接求梯度，也可以发现LSTM中h的梯度不是恒小于1）。

正向计算和反向求梯度

def lstm_step_forward(x, prev_h, prev_c, Wx, Wh, b):
    """
    Forward pass for a single timestep of an LSTM.

    The input data has dimension D, the hidden state has dimension H, and we use
    a minibatch size of N.

    Inputs:
    - x: Input data, of shape (N, D)
    - prev_h: Previous hidden state, of shape (N, H)
    - prev_c: previous cell state, of shape (N, H)
    - Wx: Input-to-hidden weights, of shape (D, 4H)
    - Wh: Hidden-to-hidden weights, of shape (H, 4H)
    - b: Biases, of shape (4H,)

    Returns a tuple of:
    - next_h: Next hidden state, of shape (N, H)
    - next_c: Next cell state, of shape (N, H)
    - cache: Tuple of values needed for backward pass.
    """
    next_h, next_c, cache = None, None, None
    #############################################################################
    # TODO: Implement the forward pass for a single timestep of an LSTM.        #
    # You may want to use the numerically stable sigmoid implementation above.  #
    #############################################################################
    H=Wh.shape[0]
    a = np.dot(x, Wx) + np.dot(prev_h, Wh) + b    # (1)
    i = sigmoid(a[:, 0:H])                # (2-5)
    f = sigmoid(a[:, H:2*H])
    o = sigmoid(a[:, 2*H:3*H])
    g = np.tanh(a[:, 3*H:4*H])
    next_c = f * prev_c + i * g           # (6)
    next_h = o * np.tanh(next_c)          # (7)

    cache = (i, f, o, g, x, Wx, Wh, prev_c, prev_h,next_c)
    
    return next_h, next_c, cache


def lstm_step_backward(dnext_h, dnext_c, cache):
    """
    Backward pass for a single timestep of an LSTM.

    Inputs:
    - dnext_h: Gradients of next hidden state, of shape (N, H)
    - dnext_c: Gradients of next cell state, of shape (N, H)
    - cache: Values from the forward pass

    Returns a tuple of:
    - dx: Gradient of input data, of shape (N, D)
    - dprev_h: Gradient of previous hidden state, of shape (N, H)
    - dprev_c: Gradient of previous cell state, of shape (N, H)
    - dWx: Gradient of input-to-hidden weights, of shape (D, 4H)
    - dWh: Gradient of hidden-to-hidden weights, of shape (H, 4H)
    - db: Gradient of biases, of shape (4H,)
    """
    dx, dh, dc, dWx, dWh, db = None, None, None, None, None, None
    #############################################################################
    # TODO: Implement the backward pass for a single timestep of an LSTM.       #
    #                                                                           #
    # HINT: For sigmoid and tanh you can compute local derivatives in terms of  #
    # the output value from the nonlinearity.                                   #
    #############################################################################
    
    
    
    i, f, o, g, x, Wx, Wh, prev_c, prev_h,next_c =cache
    
    do=dnext_h*np.tanh(next_c)
    dnext_c+=o*(1-np.tanh(next_c)**2)*dnext_h
    di,df,dg,dprev_c=dnext_c*(g,prev_c,i,f)
    da=np.hstack([i*(1-i)*di,f*(1-f)*df,o*(1-o)*do,(1-g*g)*dg])
    
    dx=np.dot(da,Wx.T)
    dWx=np.dot(x.T,da)
    dprev_h=np.dot(da,Wh.T)
    dWh=np.dot(prev_h.T,da)
    db=np.sum(da,axis=0)
    
    return dx, dprev_h, dprev_c, dWx, dWh, db


def lstm_forward(x, h0, Wx, Wh, b):
    """
    Forward pass for an LSTM over an entire sequence of data. We assume an input
    sequence composed of T vectors, each of dimension D. The LSTM uses a hidden
    size of H, and we work over a minibatch containing N sequences. After running
    the LSTM forward, we return the hidden states for all timesteps.

    Note that the initial cell state is passed as input, but the initial cell
    state is set to zero. Also note that the cell state is not returned; it is
    an internal variable to the LSTM and is not accessed from outside.

    Inputs:
    - x: Input data of shape (N, T, D)
    - h0: Initial hidden state of shape (N, H)
    - Wx: Weights for input-to-hidden connections, of shape (D, 4H)
    - Wh: Weights for hidden-to-hidden connections, of shape (H, 4H)
    - b: Biases of shape (4H,)

    Returns a tuple of:
    - h: Hidden states for all timesteps of all sequences, of shape (N, T, H)
    - cache: Values needed for the backward pass.
    """
    h, cache = None, None
    #############################################################################
    # TODO: Implement the forward pass for an LSTM over an entire timeseries.   #
    # You should use the lstm_step_forward function that you just defined.      #
    #############################################################################
    N,T,D=x.shape
    H=h0.shape[1]
    h=np.zeros((N,T,H))
    cache={}
    prev_h=h0
    prev_c=np.zeros((N,H))
    
    for t in range(T):
        xt=x[:,t,:]
        next_h,next_c,cache[t]=lstm_step_forward(xt,prev_h,prev_c,Wx,Wh,b)
        prev_h=next_h
        prev_c=next_c
        h[:,t,:]=prev_h
    
    return h, cache


def lstm_backward(dh, cache):
    """
    Backward pass for an LSTM over an entire sequence of data.]

    Inputs:
    - dh: Upstream gradients of hidden states, of shape (N, T, H)
    - cache: Values from the forward pass

    Returns a tuple of:
    - dx: Gradient of input data of shape (N, T, D)
    - dh0: Gradient of initial hidden state of shape (N, H)
    - dWx: Gradient of input-to-hidden weight matrix of shape (D, 4H)
    - dWh: Gradient of hidden-to-hidden weight matrix of shape (H, 4H)
    - db: Gradient of biases, of shape (4H,)
    """
    dx, dh0, dWx, dWh, db = None, None, None, None, None
    #############################################################################
    # TODO: Implement the backward pass for an LSTM over an entire timeseries.  #
    # You should use the lstm_step_backward function that you just defined.     #
    #############################################################################
    N, T, H = dh.shape
    D = cache[0][4].shape[1]

    dprev_h = np.zeros((N, H))
    dprev_c = np.zeros((N, H))
    dx = np.zeros((N, T, D))
    dh0 = np.zeros((N, H))
    dWx= np.zeros((D, 4*H))
    dWh = np.zeros((H, 4*H))
    db = np.zeros((4*H,))

    for t in range(T):
        t = T-1-t
        step_cache = cache[t]
        dnext_h = dh[:,t,:] + dprev_h
        dnext_c = dprev_c
        dx[:,t,:], dprev_h, dprev_c, dWxt, dWht, dbt = lstm_step_backward(dnext_h, dnext_c, step_cache)
        dWx, dWh, db = dWx+dWxt, dWh+dWht, db+dbt

    dh0 = dprev_h 
    
    return dx, dh0, dWx, dWh, db

剩下的代码和昨天几乎没有区别，还有昨天代码中留下了一个问题，现在应该也能轻松解答了吧hhh。

 

参考：

https://blog.csdn.net/zhaojc1995/article/details/80572098

http://cs231n.github.io