视频时间序列分类方法：动态时间规整算法DTW和R语言实现|附代码数据

Posted 大数据部落

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了视频时间序列分类方法：动态时间规整算法DTW和R语言实现|附代码数据相关的知识，希望对你有一定的参考价值。

原文链接：http://tecdat.cn/?p=22945

最近我们被客户要求撰写关于动态时间规整算法的研究报告，包括一些图形和统计输出

动态时间扭曲算法何时、如何以及为什么可以有力地取代常见的欧几里得距离，以更好地对时间序列数据进行分类

时间序列分类的动态时间扭曲

使用机器学习算法对时间序列进行分类需要一定的熟悉程度。

时间序列分类（TSC）任务通常由监督算法解决，它旨在创建分类器，将输入时间序列映射到描述时间序列本身的一个或多个特征的离散变量（类）中。

可以在语音识别或手势和运动识别中找到时序分类任务的有趣示例。

图 — 移动识别示例

用于其他类型的数据（例如表格数据）的标准分类算法不能直接应用，因为它们将每个样本与其他样本分开处理。

对于时间序列，不能忽略数据的时间顺序，因此，不能考虑时间序列的每个样本而考虑其他样本，但必须保留时间顺序。

出于这个原因，在文献中，有几种类型的时间序列分类技术，将在下一段中简要解释。

时间序列分类方法

作为TSC不同类型方法的简要概述。

  • 基于区间的方法：从不同的区间中提取时间序列的特征和信息，并将标准分类器应用于特征本身。算法的一个示例是时序森林分类器。
  • 基于字典 的方法：将时间序列的特征转换为代表类的单词。标准分类器应用于提取单词的分布。算法的一个例子是模式袋。
  • 基于频率的方法：在频谱水平上提取时间序列的特征，通过频率分析和连续的标准分类器。算法的一个示例是随机间隔频谱集成。
  • 基于形状的方法：形状是代表类的时间序列的子序列。提取时间序列中k个最具特征的形状，然后使用标准分类器。算法的一个示例是 Shapelet 变换分类器。
  • 集成方法：对于一般问题非常有竞争力，它们结合了几个估计器，例如HIVE-COTE算法。

基于距离的方法

在本文中，我们将重点介绍基于距离的方法。

它是一种将距离度量与分类器混合以确定类成员的非参数方法。分类器通常是 k 最近邻 （KNN）  算法，用于了解要标记的时间序列是否与训练数据集中的某些时间序列相似。根据邻域，最近的类或最近类的聚合与所分析的时间序列相关联。动态时间扭曲（DTW）是基于距离的方法的一个示例。

 图  — 基于距离的方法

距离指标

在时间序列分类中，我们需要计算两个序列之间的距离，同时牢记每个序列内样本之间的时间关系和依赖性。选择正确的指标是这种方法的基础。

欧几里得距离

让我们开始考虑常见的欧几里得距离。

鉴于时间序列分类，欧几里得距离是不合适的，因为即使它保留了时间顺序，它也以逐点的方式测量距离。实际上，与两个时间序列的欧几里得距离的相似性是通过考虑它们的振幅来计算的，而与相移、时移和失真无关。

以图中的示例为例。我们有树时间序列：ts1、ts2 和 ts3。我们希望检测两条正弦曲线彼此相似，因为它们具有相同的形状和上下趋势，即使它们的相位和频率略有不同。但是，如果我们计算欧几里得指标，直线 ts3 的结果更接近 ts1。

 图 — 要比较的时间序列示例

之所以出现这种现象，是因为欧几里得距离正在比较曲线的振幅，而不允许任何时间拉伸。

 图 — 欧几里得匹配

动态时间扭曲

引入了动态时间扭曲以避免欧几里得距离的问题。

从历史上看，它是为语音识别而引入的。如图所示，以不同的速度重复相同的句子，有必要将时间序列与相同的单词相关联，从而管理不同的速度。

 图 — DTW 的语音识别应用

DTW 允许您通过确定时间序列之间的最佳对齐方式并最大程度地减少时间失真和偏移的影响来衡量时间序列之间的相似性。

不同相的相似形状，及时匹配弹性翘曲。

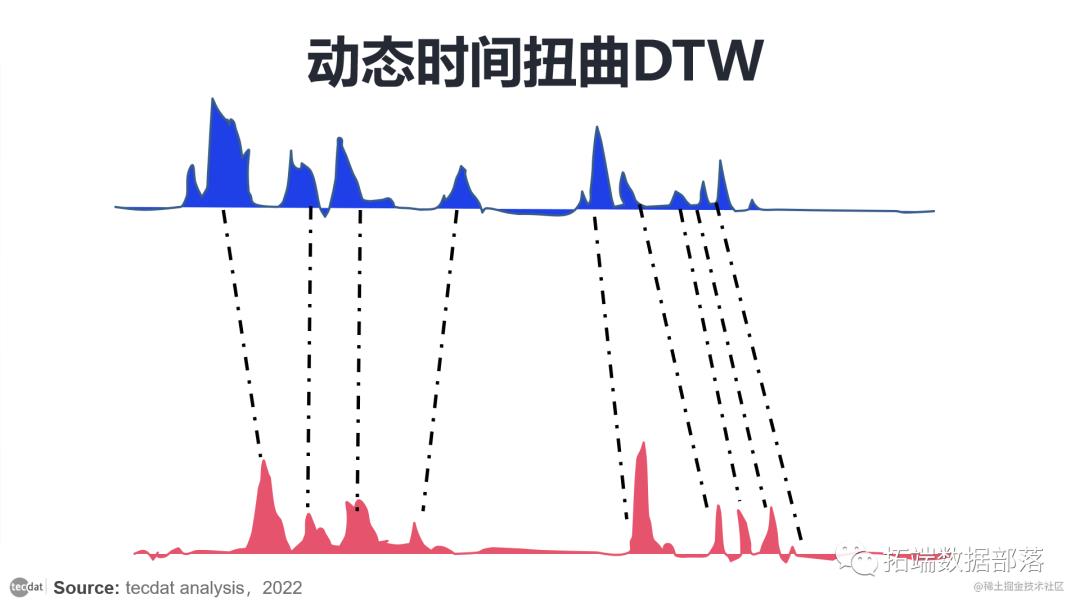
图 — 动态时间扭曲匹配

算法

让我们考虑两个时间序列 X = （x₁， x₂， ...， xn） 和 Y = （y₁， y₂， ...， ym）， 在等距时间点采样，长度相等或不同。

我们的目标是找到对齐时间序列的最小距离。

 图 — 要对齐的时间序列示例

定义局部成本矩阵，该矩阵将被最小化以找到最佳对齐方式。成本矩阵 C 定义为所有时间序列点的成对距离：

图 — 当地成本矩阵 C

目的是通过遵循成本最低的路线，在局部成本矩阵上找到对齐时间序列的翘曲路径。

翘曲路径 p 是局部成本矩阵上的点序列，因此是两个时间序列上的几个点序列：

必须满足一些条件：

  • 边界条件：

翘曲路径的起点和终点必须是序列的第一个和最后一个点。

  • 单调性条件：

以保留时间顺序。

  • 步长条件：

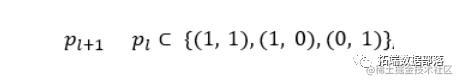
以限制跳跃和时间偏移，同时对齐序列。

每个翘曲路径都有相关的成本：

  • 与翘曲路径 p 相关的成本函数

 图 — 翘曲路径示例（非最佳）

目的是找到最佳的翘曲路径：

DTW 通过递归实现解决，为此可以找到成本最低的翘曲路径：

 

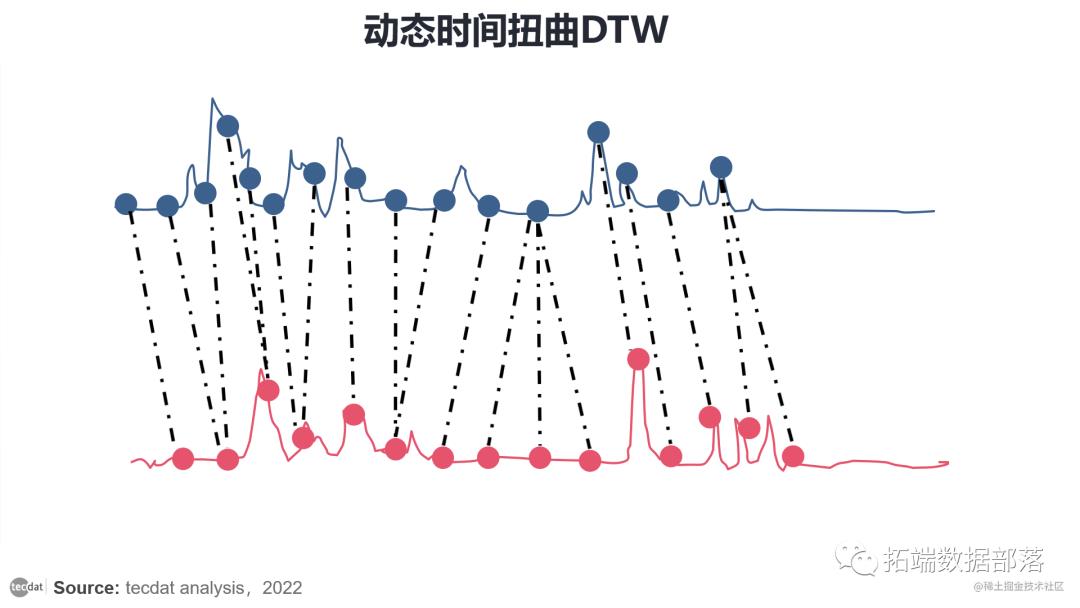 图 — 最佳翘曲路径

找到最佳翘曲路径后，将计算出相关的最优成本，并将其用作 DTW 距离。

递归实现达到最优，但计算成本为 O（NM）， 其中 N 和 M 是两个时间序列的长度。

k-最近邻

回到对感兴趣的时间序列进行分类的原始问题，距离度量可以与k-最近邻（k-nn）算法耦合。这意味着您可以计算时间序列到训练数据集中所有其他时间序列的 DTW 距离。然后，如果您正在考虑使用 1-nn 方法，则可以将最近邻的类与时间序列相关联，或者，同样，您可以将 k 最近类中最常用的类与 k-nn 方法相关联。

通过这种方式，您已经达到了为时间序列分配类的目标，该方法考虑了时间序列的时移。

传统 DTW 的替代方法可加快速度

快速 DTW

提出了一种多级方法来加快FastDTW算法中的算法速度。

它需要不同的步骤：

  • 粗化： 将时间序列缩小为较粗的时间序列。这通过对相邻点对求平均值来减小时间序列的大小。

  • 投影： 找到最小距离的翘曲路径，用作更高分辨率翘曲路径的初始猜测。

  • 优雅： 通过局部调整将翘曲路径从较低分辨率细化到较高分辨率。此步骤在投影路径的邻域中查找最佳翘曲路径，半径 r 参数控制邻域的大小。

 图 — 快速 DTW

FastDTW允许快速分辨率，复杂度为O（Nr）， 具有良好的次优解决方案。

R语言实现

在这篇文章中，我们将学习如何找到两个数字序列数据的排列。

创建序列数据

首先，我们生成序列数据，并在一个图中将其可视化。

plot(a, type = "l")
lines(b, col = "blue")

点击标题查阅往期内容

Python用KShape对时间序列进行聚类和肘方法确定最优聚类数k可视化

左右滑动查看更多

01

02

03

04

计算规整方式

dtw()函数计算出一个最佳规整方式。

align(a, b)

返回以下项目。你可以参考str()函数来了解更多信息。

现在，我们可以绘制组合。

用双向的方法作图

动态时间规整结果的绘图：点比较

显示查询和参考时间序列以及它们的排列方式，进行可视化检查。

Plot(align)

用密度作图

显示叠加了规整路径的累积成本密度 。

该图是基于累积成本矩阵的。它将最优路径显示为全局成本密度图中的 "山脊"。

PlotDensity(align)

小结

总而言之, DTW是一种非常有用的计算序列最小距离的方法, 不论是在语音序列匹配, 股市交易曲线匹配, 还是DNA碱基序列匹配等等场景, 都有其大展身手的地方. 它的最大特点是在匹配时允许时间上的伸缩, 因此可以更好的在一堆序列集合中找到最佳匹配的序列.

  1. Eamonn Keogh, Chotirat Ann Ratanamahatana, Exact indexing of dynamic time warping, Knowledge and Information Systems, 2005.

点击文末 “阅读原文”

获取全文完整资料。

本文选自《R语言DTW(Dynamic Time Warping) 动态时间规整算法分析序列数据和可视化》。

点击标题查阅往期内容

ARMA-GARCH-COPULA模型和金融时间序列案例
时间序列分析：ARIMA GARCH模型分析股票价格数据
GJR-GARCH和GARCH波动率预测普尔指数时间序列和Mincer Zarnowitz回归、DM检验、JB检验
【视频】时间序列分析：ARIMA-ARCH / GARCH模型分析股票价格
时间序列GARCH模型分析股市波动率
PYTHON用GARCH、离散随机波动率模型DSV模拟估计股票收益时间序列与蒙特卡洛可视化
极值理论 EVT、POT超阈值、GARCH 模型分析股票指数VaR、条件CVaR：多元化投资组合预测风险测度分析
Garch波动率预测的区制转移交易策略
金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格
R语言风险价值：ARIMA，GARCH，Delta-normal法滚动估计VaR（Value at Risk）和回测分析股票数据
R语言GARCH建模常用软件包比较、拟合标准普尔SP 500指数波动率时间序列和预测可视化
Python金融时间序列模型ARIMA 和GARCH 在股票市场预测应用
MATLAB用GARCH模型对股票市场收益率时间序列波动的拟合与预测R语言GARCH-DCC模型和DCC（MVT）建模估计
Python 用ARIMA、GARCH模型预测分析股票市场收益率时间序列
R语言中的时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格
R语言ARIMA-GARCH波动率模型预测股票市场苹果公司日收益率时间序列
Python使用GARCH，EGARCH，GJR-GARCH模型和蒙特卡洛模拟进行股价预测
R语言时间序列GARCH模型分析股市波动率
R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
Python使用GARCH，EGARCH，GJR-GARCH模型和蒙特卡洛模拟进行股价预测
使用R语言对S＆P500股票指数进行ARIMA + GARCH交易策略
R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模
R语言股票市场指数：ARMA-GARCH模型和对数收益率数据探索性分析
R语言多元Copula GARCH 模型时间序列预测
R语言使用多元AR-GARCH模型衡量市场风险
R语言中的时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格
R语言用Garch模型和回归模型对股票价格分析
GARCH（1,1），MA以及历史模拟法的VaR比较
matlab估计arma garch 条件均值和方差模型R语言POT超阈值模型和极值理论EVT分析

DTW (Dynamic Time Warping) 动态时间规整

在时间序列中，需要比较相似性的两段时间序列的长度可能并不相等，比较显著的例子是在语音识别领域表现为语速不同，不同人的语速不同，同一个人说同一句话的语速也会不同，那如何计算时间序列下的相似度呢？这时候会发现欧式距离有点失效了，因为长度不一致了，这时候就出现了DTW算法，它相当于对某个时间序列在时间轴进行了某种扭曲(Warping), 达到一定程度的对齐再计算相似度。

DTW可以计算两个时间序列的相似度，尤其适用于不同长度、不同节奏的时间序列（比如不同的人读同一个词的音频序列）。DTW将自动warping扭曲 时间序列（即在时间轴上进行局部的缩放），使得两个序列的形态尽可能的一致，得到最大可能的相似度。

DTW采用了动态规划DP（dynamic programming）的方法来进行时间规整的计算，可以说，动态规划方法在时间规整问题上的应用就是DTW。

下面测试程序显示了 6组时间序列 的DTW结果，左上和右下的两组相似度较高，其DTW计算的距离（Warping Distance）也确实比较小。

技术图片

 

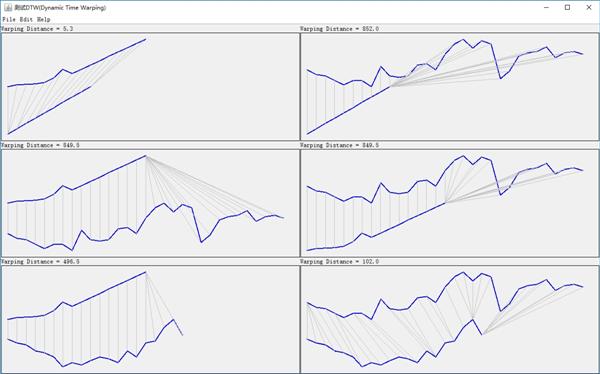
DTW加速

  DTW虽然使用线性规划可以快速的求解，但是在面对比较长的时间序列是，O(N2)的时间复杂度还是很大。已经有很多改进的快速DTW算法，比如FastDTW,SparseDTW,LB_Keogh,LB_Improved等等。

 

参考文献：

  [1]. FastDTW: Toward Accurate Dynamic Time Warping in Linear Time and Space. Stan Salvador, Philip Chan. 

  [2]. Wikipedia: Dynamic Time Warping

  [3]. Speech Recognition: 11.2 Dynamic Time Warping

https://www.jianshu.com/p/4c905853711c
https://blog.csdn.net/lin_limin/article/details/81241058
https://blog.csdn.net/ZHUQIUSHI123/article/details/84453560
https://blog.csdn.net/zouxy09/article/details/9140207
 https://www.cnblogs.com/luxiaoxun/archive/2013/05/09/3069036.html
https://github.com/davidmoten/fastdtw/tree/master/src
 

以上是关于视频时间序列分类方法：动态时间规整算法DTW和R语言实现|附代码数据的主要内容，如果未能解决你的问题，请参考以下文章

动态时间规整算法（DTW）原理即代码实现

离散序列的一致性度量方法：动态时间规整（DTW）

动态时间规整（DTW） 转载

DTW (Dynamic Time Warping) 动态时间规整

使用 dtwclust 进行动态时间规整距离 (DTW) 的时间序列聚类

DTW 笔记： Dynamic Time Warping 动态时间规整 （&DTW的python实现）