用python对股票期货做时序分析
Posted TimoTong
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了用python对股票期货做时序分析相关的知识,希望对你有一定的参考价值。
选择期货CFFEX.IF1808,截止到当日的1000条收盘价格走势:
# encoding: utf-8 import talib from talib.abstract import SMA import numpy as np import pandas as pd import math import datetime from collections import deque from gm.api import * #掘金 import matplotlib.pyplot as plt import matplotlib as mpl import mpl_finance as mpf import matplotlib.dates as mpd import seaborn as sns import statsmodels.tsa.stattools as ts import statsmodels.api as sm from statsmodels.tsa.arima_model import ARMA from scipy import stats from statsmodels.graphics.api import qqplot set_token(\'****************************\') #自行填写自己的token
now=datetime.datetime.now().date() last_day=get_previous_trading_date(exchange=\'SHSE\',date=now) index_futures=get_continuous_contracts(csymbol=\'CFFEX.IF\',start_date=last_day,end_date=last_day) #print index_futures strike_info=history_n(symbol=\'CFFEX.IF1808\',frequency=\'60s\',end_time=\'2018-07-01\',fields=\'symbol,close,frequency,cum_volume\',count=1000,df=True) strike_info.dropna() price=np.array(strike_info[\'close\'])
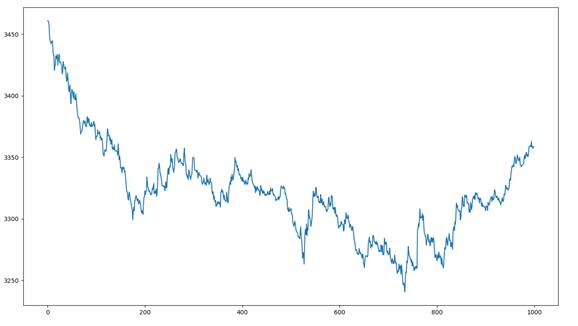
一个时间序列,他可能是有趋势的,是不平稳的,所以如果不平稳需要做差分。
ADF检测结果:
95%置信区间,p=0.0076,99%置信区间下,p=-3.5。对模型做一阶差分,希望得到一个平稳的时间序列
一阶差分后,模型基本平稳:
p=ts.adfuller(strike_info[\'close\'])[0] #print p price_log=strike_info[\'close\'].diff()

AR(p)模型,PACF会在lag=p时截尾,也就是,PACF图中的值落入宽带区域中。
MA(q)模型,ACF会在lag=q时截尾,同理,ACF图中的值落入宽带区域中。
用ACF(自相关系数)或者PACF(偏自相关系数)观察模型:
fig = plt.figure(figsize=(12,8)) ax1=fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(strike_info[\'close\'],lags=40,ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(strike_info[\'close\'],lags=40,ax=ax2) plt.show()
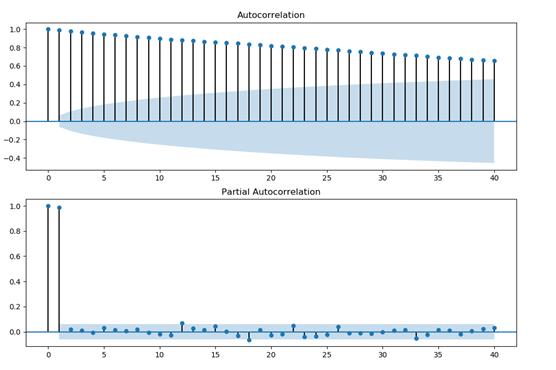
优先选择PACF图,因为PACF大约在lag=1时截尾,即PACF的值落入宽带区域中
选择AR(P=1)的模型进行自回归拟合,得到拟合效果:
arma_mod80 = sm.tsa.ARMA(strike_info[\'close\'],(1,0)).fit() print(arma_mod80.aic,arma_mod80.bic,arma_mod80.hqic) resid = arma_mod80.resid print(sm.stats.durbin_watson(arma_mod80.resid.values)) print(stats.normaltest(resid)) fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) fig = qqplot(resid, line=\'q\', ax=ax, fit=True) plt.show()
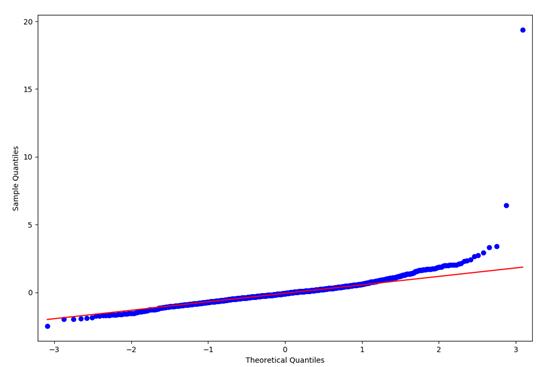
检验:计算得到序列的残差,基本为白噪音
fig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=40, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax2) plt.show()

用自回归拟合的模型进行预测,结果如下:
fig=plt.figure(figsize=(15,7)) price2=strike_info=history_n(symbol=\'CFFEX.IF1808\',frequency=\'60s\',end_time=\'2018-07-01\',fields=\'symbol,close,frequency,cum_volume\',count=1000,df=True)[\'close\'] price3=strike_info=history_n(symbol=\'CFFEX.IF1808\',frequency=\'60s\',end_time=now,fields=\'symbol,close,frequency,cum_volume\',count=1000,df=True)[\'close\'] print len(price2) fit = arma_mod80.predict(0, 1100) plt.plot(range(1100),fit[:1100],label=\'predict\') plt.plot(price2,label=\'price\') plt.legend(loc=4) plt.show()
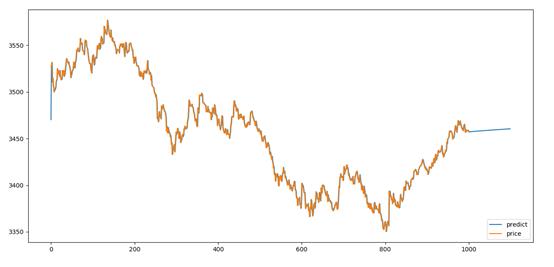
以上是关于用python对股票期货做时序分析的主要内容,如果未能解决你的问题,请参考以下文章