计算机科学速成科听课随笔5

Posted 2023-05-07 naoziinicu

计算机网络

计算机近距离构成的小型网络叫做 局域网，简称LAN，小到一间屋子里的几个机子，大到一个校园里的电脑都在一个局域网中

最成功的局域网叫做 以太网

以太网的最简单形式就是用一根电线，将所有电脑连在一起，将所有数据以电线为载体，电信号的形式发送，由于电线是共享的，所以只要发送数据，发出来的数据会被连在一起的所有电脑都接收

由于全部接收对于一些计算机是多余的，以太网创造了 MAC地址（每一个计算机唯一的媒体访问控制地址）。作为数据的前缀发送，接收时检查是否是自己的MAC地址，再看接不接收

多台电脑共享一个传输媒介这个方法叫做 载波侦听多路访问 简称 CSMA
如，以太网的载体是铜线，WIFI的载体是空气

由于有共同载体，当多个计算机同时像发送数据时，就会造成 冲突
最容想到的方法就是停一会，但是其他计算机也可能停止了相同的时间，才开始传输，再次造成了冲突
可以用一个小技巧，叫做 指数退避
简单来说就是第一次停一秒，第二次停两秒。第三次停四秒。。。

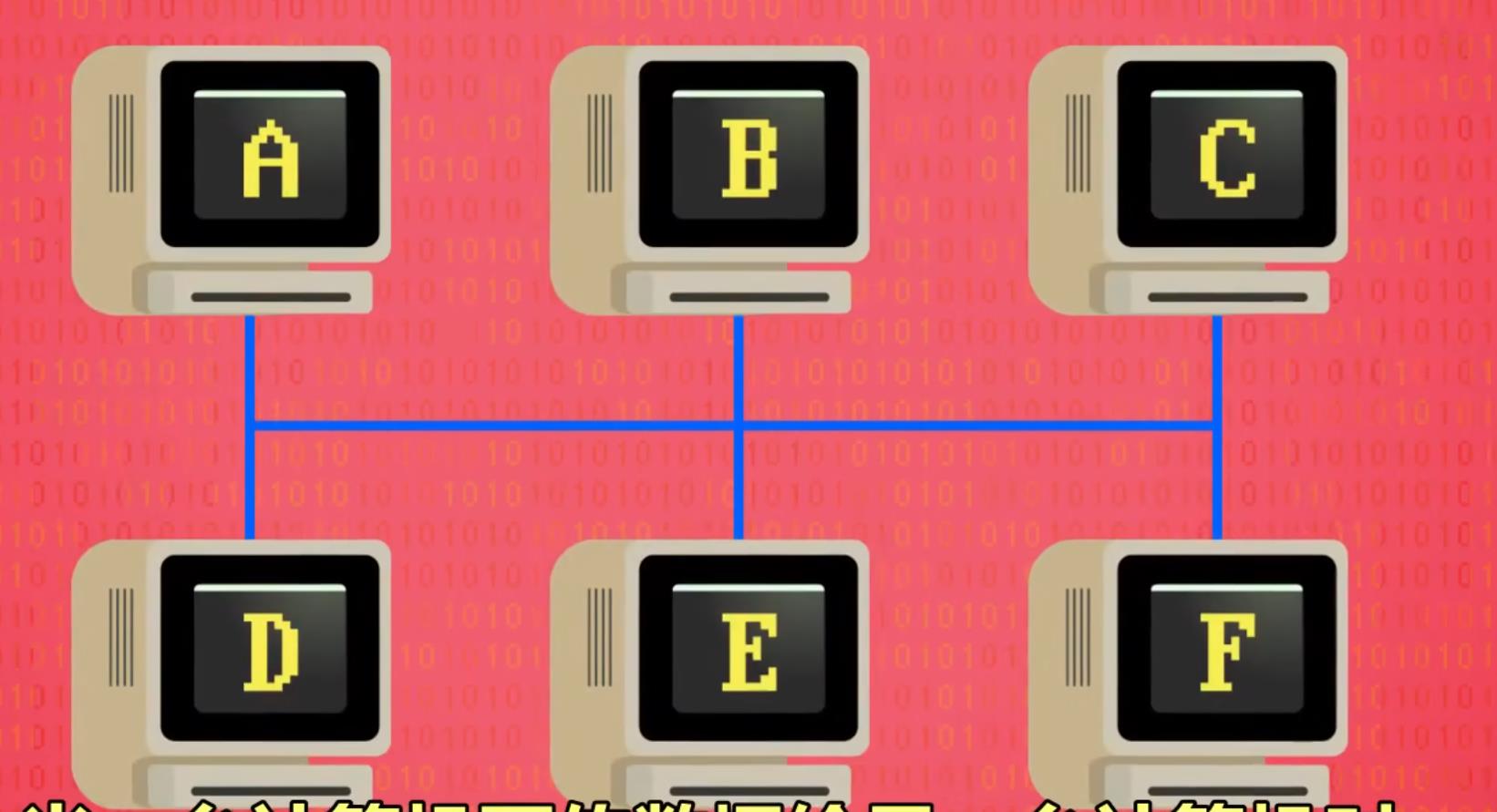
到此为止，还是不够产生大范围，高效率的局域网，我们需要减少同一载体中设备数量，载体和其中的设备总称为 冲突域

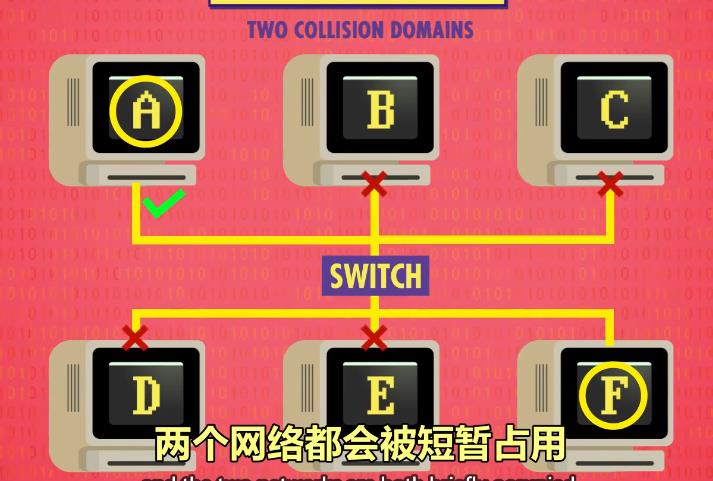
我们可以用交换机来，将大范围的两个冲突域拆分为两个小的冲突域，但交换机必须位于两个网络之间

交换机需要记录一个列表来区分每一个网络中的计算机，假如一个网络，传输数据时没有涉及到其他网络，就不会启用无关网络，避免占用但是要是用到了其他网络中的计算机，就会同时占用这几个网络

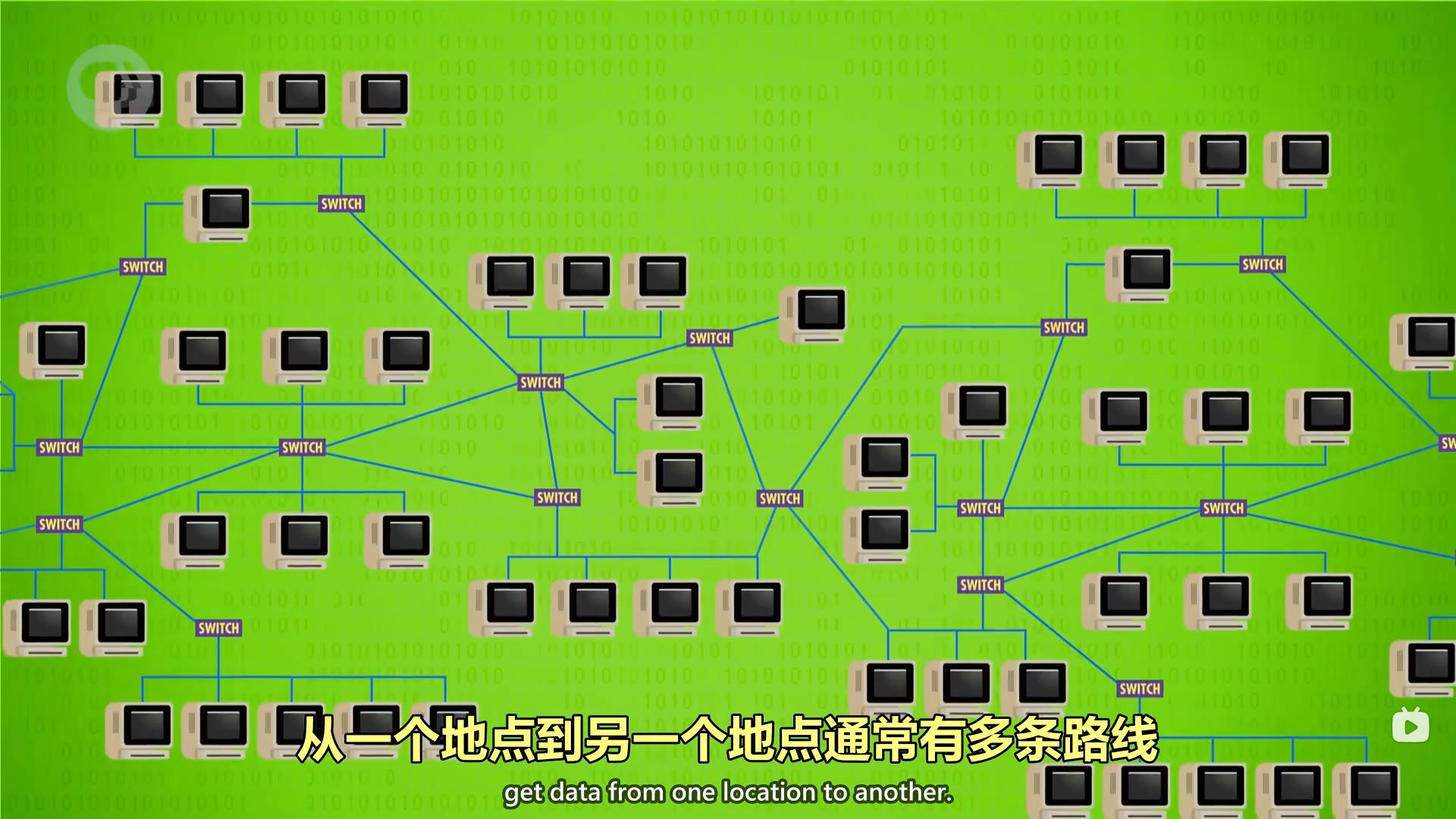
最大的网络--互联网 和这个原理差不多，不过每一个地点之间不只有一个路线
就产生了一个新概念，路由 就是将数据送到目的地
路由器会平衡与其他路由器之间的负载，以确保传输可以快速可靠，这叫做”阻塞控制“

传输数据还可以利用 报文交换 ，就像邮件一样，假如一条路由不通，可以用不同路由来使数据到达目的地，提高通信的容错率，如下图

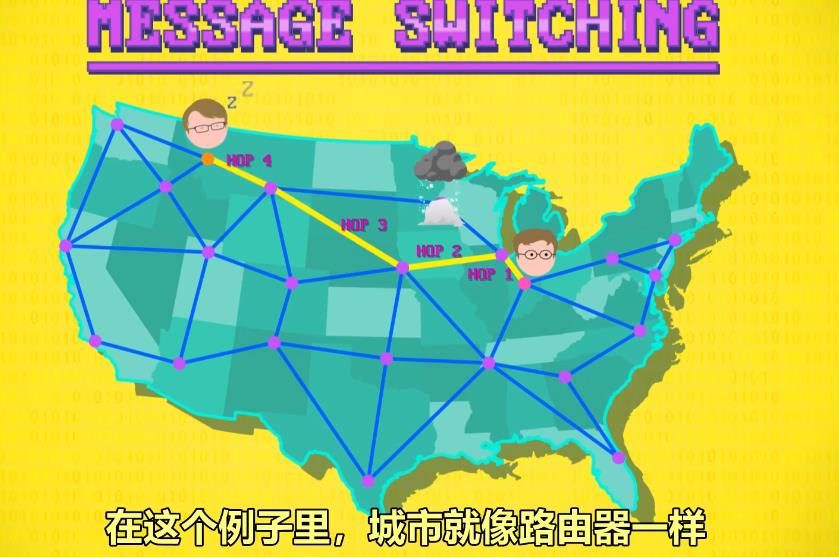
消息沿着路由跳转的次数，叫做 跳数。可以通过检查跳数的次数，来反映出一个地方的路由是否出现了问题，便于维护

但是当数据过大时，运用报文交换，会堵塞网络，因为一个文件在一个节点传输很久，会将其他来这个节点的数据堵在后面，解决方法是，将大报文分成很多小块，叫 数据包

报文的具体格式由”互联网协议“定义，简称 IP ，创建于1970年，由于文件的数据包可能到达目的的顺序不同，通过 TCP/IP ，可以解决乱序问题

互联网

由WiFi连着的所有设备组成了局域网 （LAN），局域网组成了广域网 （WAN）
广域网一般属于你的互联网服务提供商，简称 ISP

IP是非常底层的协议，只记录了数据包的目的地，以此之上，还需要一些更高级协议
如 用户数据报协议 ，简称 UDP
UDP的头部需要，一个端口号（每一个想要访问网络的程序都会向操作系统社申请一个端口号），来指定将数据包发给哪一个程序，和一个校验和，用来检查数据是否正确、完整

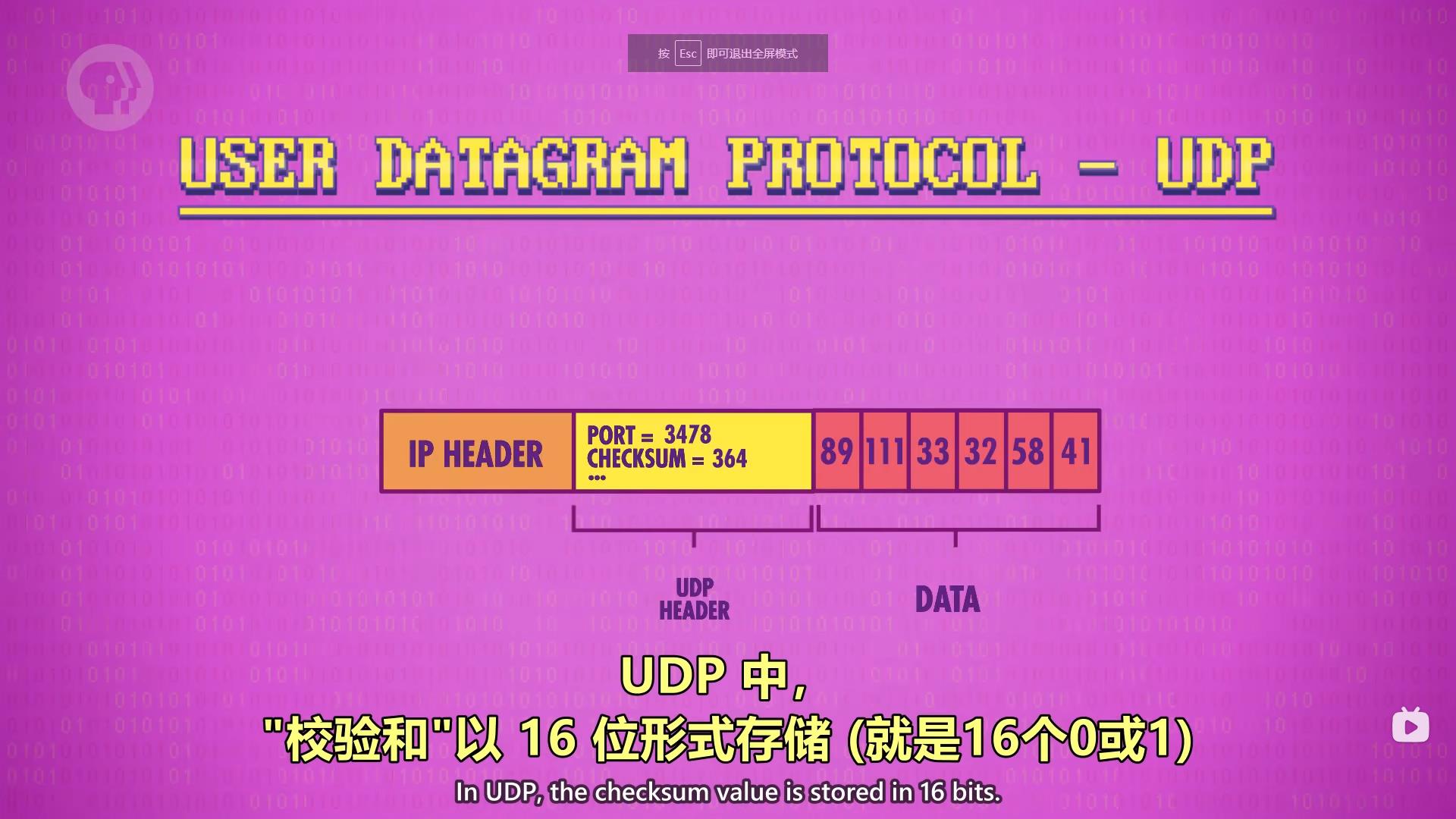
简单来说
IP 负责把数据包送到送到正确的计算机
UDP 负责包数据包送到正确的程序

UDP不包括损坏文件的自动修复，但是胜在简单且快，如果所有数据必须到达，就可以用传输控制协议，简称TCP

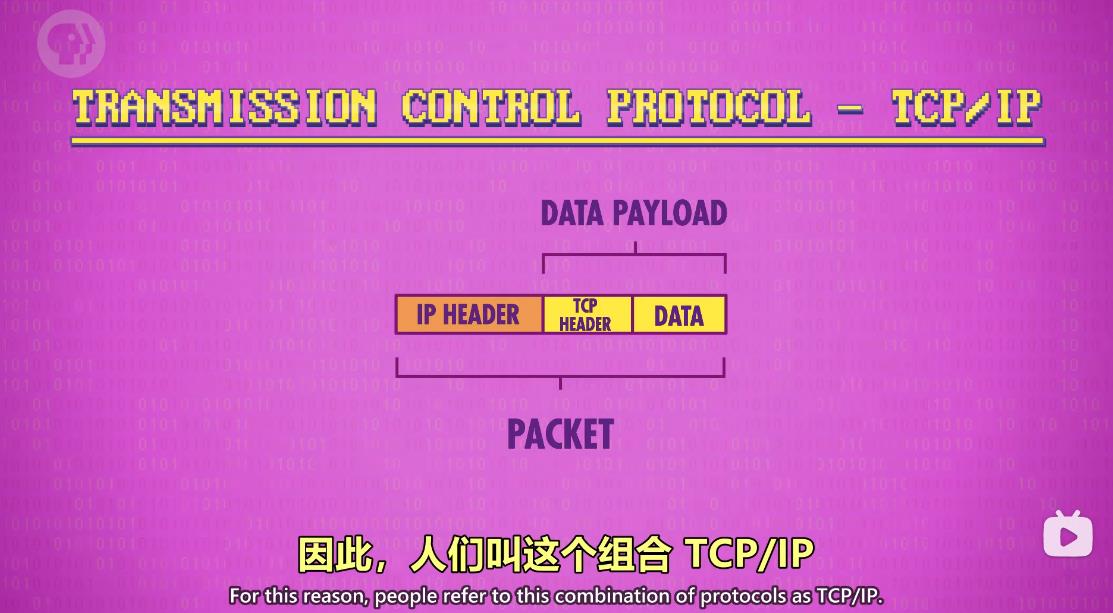
和UDP一样，TCP头部也有“端口号”和“校验和”
除此之外，TCP还有更高级的功能，如
·TCP数据包有序列号
·TCP要求接收方的电脑收到数据包并且“骄傲沿河检查无误后”，给发送方发一个确认码 ACK，代表收到了，接受成功之后才会继续发送

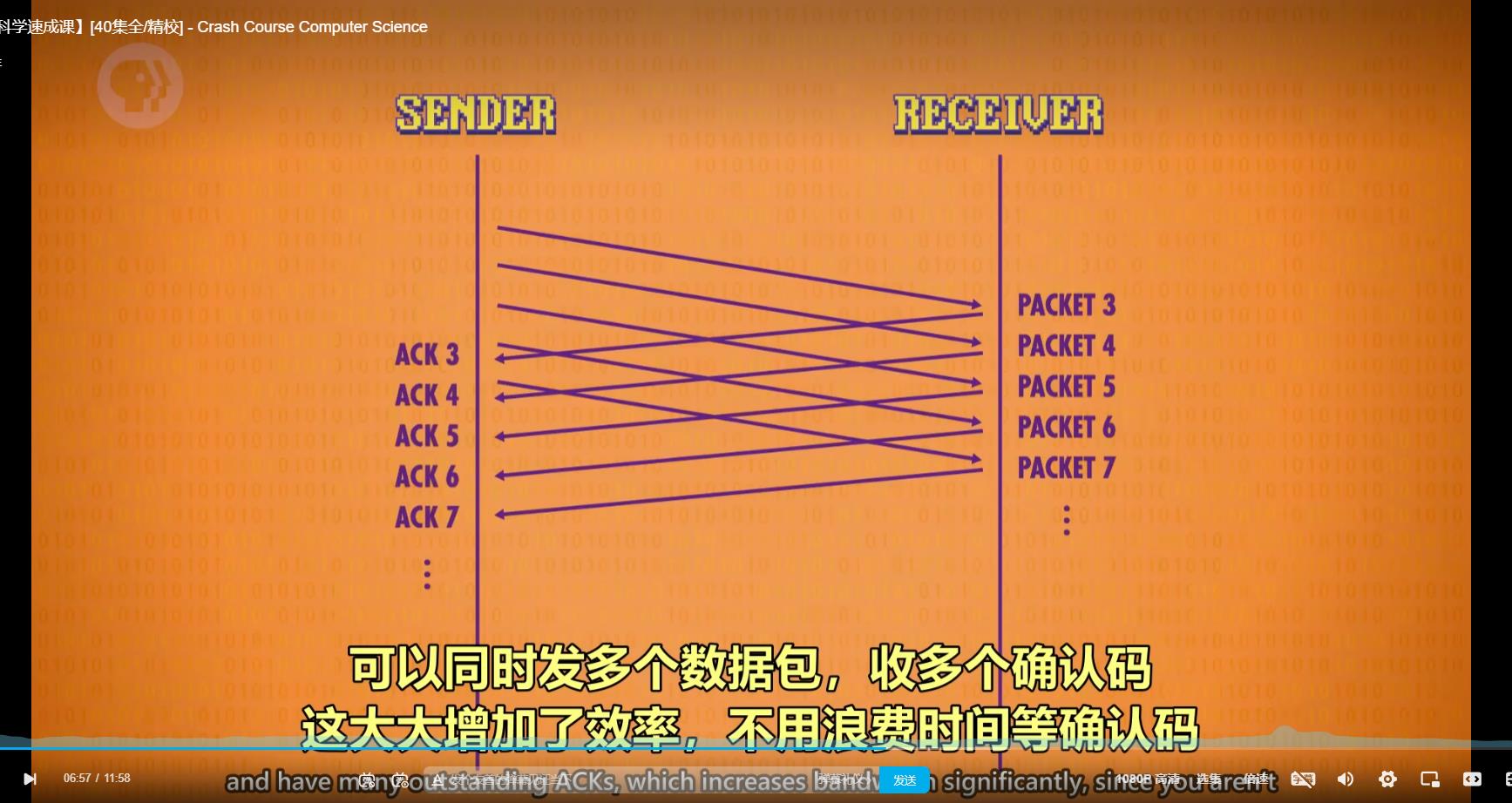
TCP还可以用确认码的成功率和来回使劲按来推测网络的拥挤程度，来调整同时发包数量，解决拥堵问题

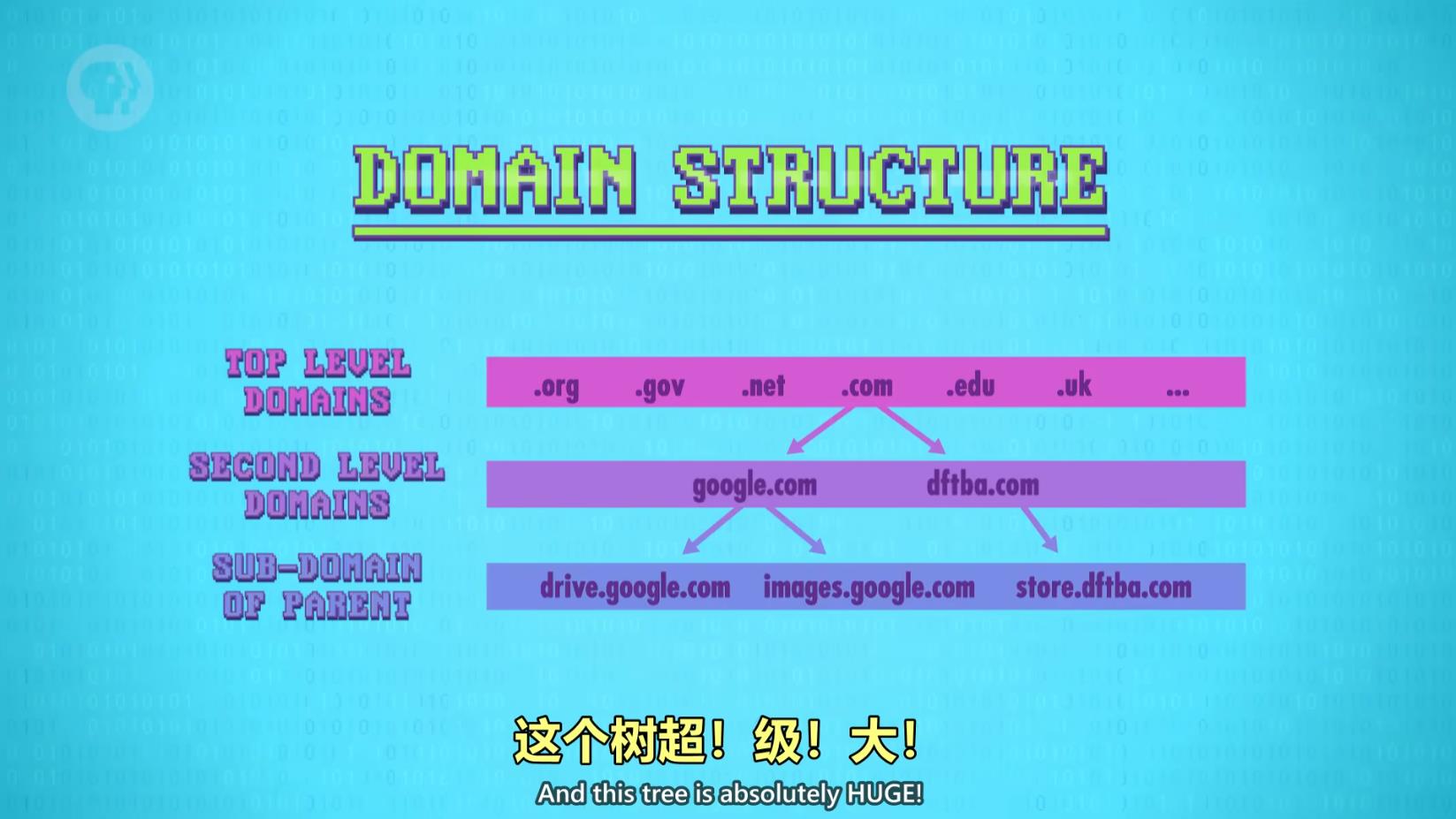
互联网还有个特殊服务，将域名和IP地址一一对应，叫做 域名系统，简称 DNS

DNS是一个树状结构，顶级域名在最顶部，下一层是二级域名，再下一层是子域名

开放式系统互通通信参考模型（OSI），一个概念性框架，将网络通信划分为许多层，一种抽象概念，在问题出现时不被整体复杂度难倒

万维网

万维网的最基本单位是单个页面，页面中有内容还有超链接，这些超链接形成的巨大的互联网络就叫做万维网

为了使网页能和相互连接，每一个网页需要一个唯一地址，这个地址叫做 统一资源定位器，简称 URL

向服务器请求打开一个页面时就会用到 超文本传输协议（HTTP），后续中HTTP添加了状态码，顾名思义代表当前的状态，状态码400~499代表客户端出错（这个时候就要提到熟悉的404了，：））

计算机科学数学[关闭]

【中文标题】计算机科学数学[关闭]

【英文标题】：Math for computer science [closed]

【发布时间】：2013-01-29 21:07:36

【问题描述】：

我已经阅读了关于这个主题的几个答案，但我仍然有问题.. 数学课很多，不知道先学哪一门。 每个计算机科学家都应该参加哪些数学课？什么课程应该是第一个，为什么？

【参考方案1】：

非常好的和重要的问题！对数学的良好理解对于每个计算机科学家来说都是必不可少的，而且数学要求也开始变得更加多样化。

Discrete Math 是计算机科学最重要和最基础的课程，因此它通常在 CS 系而不是数学系提供。本课程将巩固您对算法的介绍，并教您如何用数学方法证明事物，并为您提供分析数据结构和算法的基础知识。 Calculus 虽然不直接用于入门级计算机科学课程，但通常是您的大学提供的一系列课程，用于提高您的数学技能。但是，当您开始涉足数值编程和机器学习等领域时，它将证明非常有用。这也是高级概率/统计课程的要求。 Probability 通常在您的离散数学课程中有所涉及，但您可能希望参加关于连续概率分布的课程和 statistical inference，可能在数学和统计系。这将使您更好地了解如何进行数值计算和模拟，这对于 machine learning（计算机科学最重要的应用之一）来说是必不可少的。 Linear Algebra 是一个主要用于机器学习和（高级）算法类的课程，但它在计算机视觉、计算机图形学、机器学习和其他定量子学科中的重要性至关重要。

也就是说，如果有机器学习课程的介绍，它们可能会涵盖足够多的线性代数和其他您可以通过基本概率课程学习的内容。但是，对于计算机科学研究生而言，对上述所有数学领域的良好理解至关重要。

除了本科数学之外，高级数学课程对于计算机科学的某些理论领域（例如算法博弈论，它与经济学相交）也很有用，尤其是在超越机器学习从业者的情况下开发新算法方面。这些课程包括：

Real analysis，包括measure theory，你会发现如果你研究概率和微积分足够长的时间，它们会再次收敛。当您开始使用涉及数字的算法时，分析通常是一件有用的事情。

Optimization，包括linear optimization、convex optimization、gradient descent等。在很多情况下，“学习”一个机器学习模型基本上归结为优化一个目标函数，而这个函数的属性，比如它是否是凸的，对优化的难易程度有很大的影响。

Numerical methods：有些人不会认为这是一门数学课本身，但是在将算法和理论转化为浮点数学的不完美表示时，存在许多实际问题待解决。例如，log-sum-exp trick。

对于那些将从事“数据科学”和相关领域的人来说，高级统计，尤其是causal inference 非常重要。有很多事情要知道，主要是因为访问大量数据会吸引 this problem 为外行。

【讨论】：

我应该按照你列出的顺序学习这些课程吗？

在一所典型的四年制大学中，您将从第一年的微积分课程开始，然后在您满足 CS 课程的一些基本要求后立即学习离散数学。然后，如果您进入计算机科学更定量的子领域，您可以学习更高级的概率/统计课程和线性代数。

我认真编程已经 35 年了。当我在 Dice 上发帖时，我会在几天内收到多个 6 位数的报价。我可以从经验告诉你数学与严肃的编程几乎没有任何关系。有例外吗？当然可以，但我什至可以说，一个擅长数学的人可能是一个糟糕的程序员。

@patcapozzi 编程只是计算机科学的一小部分 :)

@patcapozzi 你是绝对正确的。编程几乎与数学无关。但关键是，编程不是计算机科学。计算机科学是关于建模、系统设计和架构、开发算法、解决问题等。实际上编程只是实现的一部分，是最后一个阶段。

【参考方案2】：

Combinatorics,numerical analysis,discrete mathematics,mathematical statistics,probability theory,information theory,linear algebra,lambda calculus,lambda calculus,mathematical logic,category theory,process calculus等p>

【讨论】：

这些都与 99% 的编程无关。如果数学如此重要，那么数学课在哪里？

我一直在应用：组合数学、离散数学、概率、数学逻辑和线性代数直接应用于编程，它们都与算法有关。

我认为计算机科学和编程经常被等同起来，但它们是不同的学科。一个人可以在没有 CS 学位的情况下学习编程，实际上只需要基础数学，因为大多数复杂的概念通常都封装在编程语言或库中。然而，这些概念的基础植根于 CS，并且需要一些不错的数学知识才能理解，尤其是在算法设计/优化方面。

【参考方案3】：

既然你指定了“计算机科学家”，我们就走硬路线：

算法分析依赖于微积分、微分方程和离散数学。 （许多人将算法分析视为计算机科学和软件工程程序之间的主要区别）。 计算机图形/科学可视化需要工程分析背景：数值方法、线性代数等。 计算几何 函数逼近 集合论、逻辑/一阶微积分 概率/统计 名单还在继续:)