「学习笔记」双连通分量割点与桥
Posted 朝气蓬勃 后生可畏
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了「学习笔记」双连通分量割点与桥相关的知识,希望对你有一定的参考价值。
文章图片全部来自 Oi-wiki,部分图片加以修改
前面我们在学 tarjan 算法时,提到过强连通分量,即有向图上的环,那么无向图上是否也有强连通分量呢?很遗憾,没有
但是,无向图有双连通分量!分为点双连通和边双连通(下面简称点双和边双)。
边双连通分量
概念
在一张联通的无向图中,对于两个点 \\(x\\) 和 \\(y\\),删去图上的任意一条边,两个点始终保持联通,则这两个点是边双连通。
边双连通分量,即极大边双连通子图,边双连通分量中的任意两点都是边双连通的,且如果加入一个不属于该子图的点,都会导致这个图不再满足两两之间边双的性质。
在无向图中。删掉一条边,导致两个图不连通了,这条边就是割边,也叫做桥。
边双连通具有传递性,即如果 \\(x\\) 与 \\(y\\) 边双连通,\\(y\\) 与 \\(z\\) 边双连通,则 \\(x\\) 与 \\(z\\) 也边双连通。
如图,在这张图中,\\(A\\) 与 \\(B\\) 边双连通,\\(B\\) 与 \\(C\\) 边双连通,根据传递性,\\(A\\) 与 \\(C\\) 边双连通。(即使不跟据传递性,他们也的确是边双连通)
找桥的过程
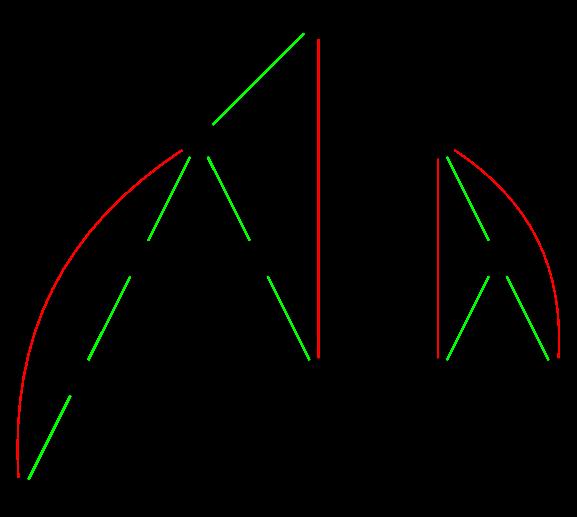
如图,绿色的边和黑色的边都是树边,红色的边是返祖边。
我们发现,每一条返祖边都对应着一条树上的简单路径,即覆盖了树上的一些边,覆盖了的边我们用绿边表示,黑色的边没有被覆盖。我们如果删去返祖边或者任意一条绿边,都不会影响图的连通性(如果删掉返祖边就从绿边走,如果删掉绿边就从返祖边走),但是,如果我们删掉黑边,那么整个图就会被一分为二,不再保持联通,这些黑色的边就是桥,同时返祖边和绿边一定不是桥。
这样,我们只要找到所有的桥,就能确定边双连通分量了。
找边双连通分量,我们可以用 tarjan 算法。
void tarjan(int u, int fa)
dfn[u] = low[u] = ++ tim; // 打上时间戳
for (int i = h[u], v; i; i = e[i].nxt)
v = e[i].v;
if ((i ^ 1) == fa) continue;
if (!dfn[v]) // 如果这个点从未被搜过
tarjan(v, i); // 继续往下搜
low[u] = min(low[u], low[v]); // 正常更新 low 值
if (low[v] > dfn[u]) // 如果 v 点无法通过返祖边向上返回到 u 点即往上
e[i].ok = e[i ^ 1].ok = 1; // 那么这条边就是桥
// 不理解的话可以想一想,v 点不管怎么向上都不能到达 u 点即更靠上的位置,那 u -> v 这条边就没有被返祖边覆盖,它就是桥
else // 如果这个点已经被搜过了(说明这条边是返祖边)
low[u] = min(low[u], dfn[v]); // 更新 low 值(比较的是 dfn[v],不是 low[v])
找边双连通分量
有两种方式,像找强连通分量那样用一个栈,或者标记桥之后再 dfs。
洛谷模板题测试,用栈比标记桥更快一些。
- 用栈找双连通分量
void tarjan(int u, int fa)
dfn[u] = low[u] = ++ tim;
sta.push_back(u);
for (auto [v, i] : son[u])
if (i == fa) continue;
if (! dfn[v])
tarjan(v, i);
low[u] = min(low[u], low[v]);
else
low[u] = min(low[u], dfn[v]);
if (dfn[u] == low[u])
ans[++ dcc].push_back(u);
while (sta.back() != u)
ans[dcc].push_back(sta.back());
sta.pop_back();
sta.pop_back();
- 标记桥,dfs。
void tarjan(int u, int fa)
dfn[u] = low[u] = ++ tim;
for (auto [v, i] : son[u])
if (i == fa) continue;
if (! dfn[v])
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u])
ok[i] = 1;
else
low[u] = min(low[u], dfn[v]);
void dfs(int u) // dfn 要清零,你也可以再开一个数组
ans[dcc].push_back(u);
dfn[u] = 1;
for (auto [v, i] : son[u])
if (dfn[v] || ok[i]) continue;
dfs(v);
点双连通分量
概念
在一张联通的无向图中,对于两个点 \\(x\\) 和 \\(y\\),删去图上的任意一个点(不能删去 \\(x\\) 和 \\(y\\)),两个点始终保持联通,则这两个点是点双连通。
删去一个点,会删掉这个点以及这个点所连接的所有的边,所以桥连接的两个点都是割点。
点双连通分量,即极大点双连通子图,点双连通分量中的任意两点都是点双连通的,且如果加入一个不属于该子图的点,都会导致这个图不再满足两两之间点双的性质。
在无向图中。删掉一个点,导致两个图不连通了,这个点就是割点。
点双连通没有传递性,即如果 \\(x\\) 和 \\(y\\) 点双联通,\\(y\\) 和 \\(z\\) 点双联通,\\(x\\) 和 \\(z\\) 不一定点双联通。
举个例子。
\\(A\\) 与 \\(B\\) 点双连通,\\(B\\) 与 \\(C\\) 点双连通,但是 \\(A\\) 与 \\(C\\) 并不是点双连通。(割点为 \\(B\\))
过程

如图,黑色的边是树边,红色的边是返祖边,每一条返祖边对应着一条简单路径。
现在,我们将每一条边看作是一个点,即图上蓝色的点,返祖边所覆盖的简单路径上的边都连上边,即图上的蓝边。
这样,要判断点是否为割点,只要判断这个点连出去的边是否在一个连通分量里,都在一个连通分量里,就不是割点,否则就是割点
这里还有另一种做法。
对于某个顶点 \\(u\\),如果存在至少一个顶点 \\(v\\),使得 low[v] \\(\\geq\\) dfn[u],即不能回到祖先,那么 \\(u\\) 点为割点。
但这个做法唯独不适用于搜索树的起始点,即搜索树的根,如果根只有一个子树,那我们把根节点删去,对图的连通性不会有任何影响,即根节点不是割点,如果根节点有着至少两个子树,那么根节点就是割点。
void tarjan(int u, int fa)
dfn[u] = low[u] = ++ cnt;
int son = 0;
for (int i = h[u], v; i; i = e[i].nxt)
v = e[i].v;
if (v == fa) continue;
if (!dfn[v])
++ son;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u])
ok[u] = 1;
++ dcc;
else
low[u] = min(low[u], dfn[v]);
if (fa == 0 && son < 2) ok[u] = 0;
应用
在题目中,桥一般出现在“给定一张无向图,问是否有一种方案,能给定向,同时保证每个点都能走到”这样类似的题目上,在这道题中,有桥就没有可行方案,倘若要输出方案,我们可以利用 dfs 生成树。
由于边双比点双有着更好的性质,所以一般题目都是有关边双的。
关于用 vector 来写 tarjan
优点:动态空间,方便。
缺点:慢!
上面的代码我们也看到了,有些题目有重边,用一般的 vector 存图方式判断是否走过重边,这里有一个方式可以实现用 vector 来找重边,那就是将 vector 的变量类型改成 pair,第一个元素存到达的节点,第二个元素存这条边的编号,如果不保险可以再开一个 vector 、结构体或两个数组来存第 \\(i\\) 条边的两个端点的编号,像这样。
e.push_back(0, 0);
for (int i = 1, x, y; i <= m; ++ i)
scanf("%d%d", &x, &y);
son[x].push_back(y, i);
son[y].push_back(x, i);
e.push_back(x, y);
这样,我们在 tarjan 判重边的的过程中可以直接判断编号了。
void tarjan(int u, int fa)
dfn[u] = low[u] = ++ tim;
for (auto [v, i] : son[u])
if (i == fa) continue;
if (! dfn[v])
tarjan(v, i);
low[u] = min(low[v], low[u]);
if (low[v] > dfn[u])
ok[i] = 1;
else
low[u] = min(low[u], dfn[v]);
对于找割点,我们直接用 vector 就行了,这里不存在任何限制,就是会慢。
void tarjan(int u, int fa)
dfn[u] = low[u] = ++ cnt;
st[++ top] = u;
int ch = 0;
for (int v : son[u])
if (v == fa) continue;
if (!dfn[v])
++ ch;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u])
ok[u] = 1;
++ dcc;
while (st[top + 1] != v)
ans[dcc].push_back(st[top --]);
ans[dcc].push_back(u);
else
low[u] = min(low[u], dfn[v]);
if (fa == 0 && ch == 0) ans[++ dcc].push_back(u);
if (fa == 0 && ch < 2) ok[u] = 0;
题目
都是来源于洛谷的模板题
P8436 【模板】边双连通分量
- 直接用栈来找边双。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 5e5 + 5;
const int M = 2e6 + 5;
int n, m, cnt = 1, tim, top, dcc;
int h[N], dfn[N], low[N];
bool ok[M];
vector<pii> son[N];
vector<int> ans[N], sta;
struct edge
int v, nxt;
bool ok;
e[M << 1];
void add(int u, int v)
e[++ cnt].nxt = h[u];
e[h[u] = cnt].v = v;
void tarjan(int u, int fa)
dfn[u] = low[u] = ++ tim;
sta.push_back(u);
for (auto [v, i] : son[u])
if (i == fa) continue;
if (! dfn[v])
tarjan(v, i);
low[u] = min(low[u], low[v]);
else
low[u] = min(low[u], dfn[v]);
if (dfn[u] == low[u])
ans[++ dcc].push_back(u);
while (sta.back() != u)
ans[dcc].push_back(sta.back());
sta.pop_back();
sta.pop_back();
int main()
scanf("%d%d", &n, &m);
for (int i = 1, x, y; i <= m; ++ i)
scanf("%d%d", &x, &y);
son[x].push_back(y, i);
son[y].push_back(x, i);
for (int i = 1; i <= n; ++ i)
if (!dfn[i])
tarjan(i, 0);
printf("%d\\n", dcc);
for (int i = 1; i <= dcc; ++ i)
int siz = ans[i].size();
printf("%d ", siz);
for (int j : ans[i])
printf("%d ", j);
putchar(\'\\n\');
return 0;
- 标记桥,通过 dfs 来找边双。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 5e5 + 5;
const int M = 2e6 + 5;
int n, m, cnt = 1, tim, top, dcc;
int h[N], dfn[N], low[N];
bool ok[M];
vector<int> ans[N];
vector<pii> son[N];
struct edge
int v, nxt;
bool ok;
e[M << 1];
void add(int u, int v)
e[++ cnt].nxt = h[u];
e[h[u] = cnt].v = v;
void tarjan(int u, int fa)
dfn[u] = low[u] = ++ tim;
for (auto [v, i] : son[u])
if (i == fa) continue;
if (! dfn[v])
tarjan(v, i);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u])
ok[i] = 1;
else
low[u] = min(low[u], dfn[v]);
void dfs(int u)
ans[dcc].push_back(u);
dfn[u] = 1;
for (auto [v, i] : son[u])
if (dfn[v] || ok[i]) continue;
dfs(v);
int main()
scanf("%d%d", &n, &m);
for (int i = 1, x, y; i <= m; ++ i)
scanf("%d%d", &x, &y);
son[x].push_back(y, i);
son[y].push_back(x, i);
for (int i = 1; i <= n; ++ i)
if (!dfn[i])
tarjan(i, 0);
memset(dfn, 0, sizeof dfn);
for (int i = 1; i <= n; ++ i)
if (!dfn[i])
++ dcc;
dfs(i);
printf("%d\\n", dcc);
for (int i = 1; i <= dcc; ++ i)
int siz = ans[i].size();
printf("%d ", siz);
for (int j : ans[i])
printf("%d ", j);
putchar(\'\\n\');
return 0;
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5 + 5;
const int M = 2e6 + 5;
int n, m, cnt, top, dcc;
int h[N], dfn[N], low[N], st[N];
bool ok[N];
vector<int> son[N], ans[N];
void tarjan(int u, int fa)
dfn[u] = low[u] = ++ cnt;
st[++ top] = u;
int ch = 0;
for (int v : son[u])
if (v == fa) continue;
if (!dfn[v])
++ ch;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u])
ok[u] = 1;
++ dcc;
while (st[top + 1] != v)
ans[dcc].push_back(st[top --]);
ans[dcc].push_back(u);
else
low[u] = min(low[u], dfn[v]);
if (fa == 0 && ch == 0) ans[++ dcc].push_back(u);
if (fa == 0 && ch < 2) ok[u] = 0;
int main()
scanf("%d%d", &n, &m);
for (int i = 1, x, y; i <= m; ++ i)
scanf("%d%d", &x, &y);
son[x].push_back(y);
son[y].push_back(x);
cnt = 0;
for (int i = 1; i <= n; ++ i)
if (!dfn[i])
top = 0;
tarjan(i, 0);
printf("%d\\n", dcc);
for (int i = 1; i <= dcc; ++ i)
printf("%d ", (int)ans[i].size());
for (int j : ans[i])
printf("%d ", j);
putchar(\'\\n\');
return 0;
求割点与桥
在学习了刘汝佳大大的蓝书后有点体会,特来小结一下.
割点:对于无向图G,如果删除某个点u后,连通分量数目增加,称u为图的割点.
桥:对于无向图G,如果删除某条边(u,v)后,连通分量数目增加,称(u,v)为图的桥.
先说说怎么求割点吧,我们可以先想怎么暴力求解:把每一个点删除一次,然后dfs看连通分量的数目的变化,不过这样复杂度O(n(n + m)),能不能优化呢?先想象一下割点是一个什么样的点:
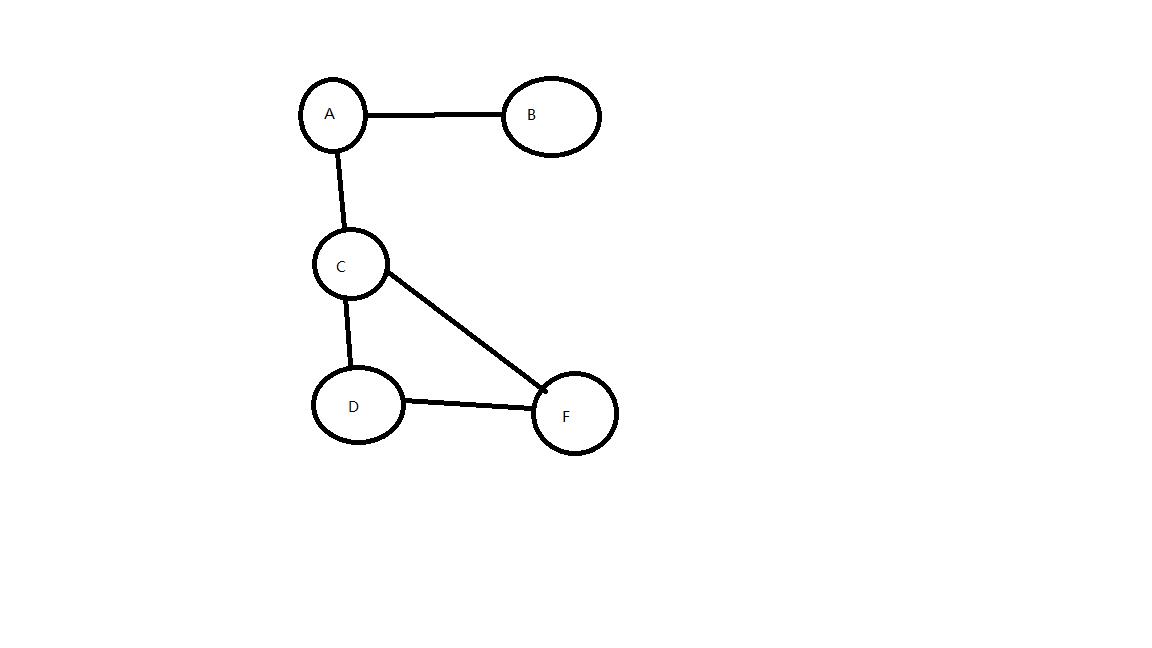
其中A很显然是割点,D不是割点,这两个点很有特点,所以我们拿它们来分析,这个图很像一棵树,其中A是根节点,我们可以猜想一下:如果一棵树的根节点有两个或两个以上个孩子,那么根节点就是割点,这个是显然的.那么D为什么不是割点呢?C是D的祖先,F是D的儿子,儿子能连一条边到祖先,所以D就不是割点。这些分析都建立在图是一棵树的基础上,可是这根本不是树啊?我们可以考虑dfs树:
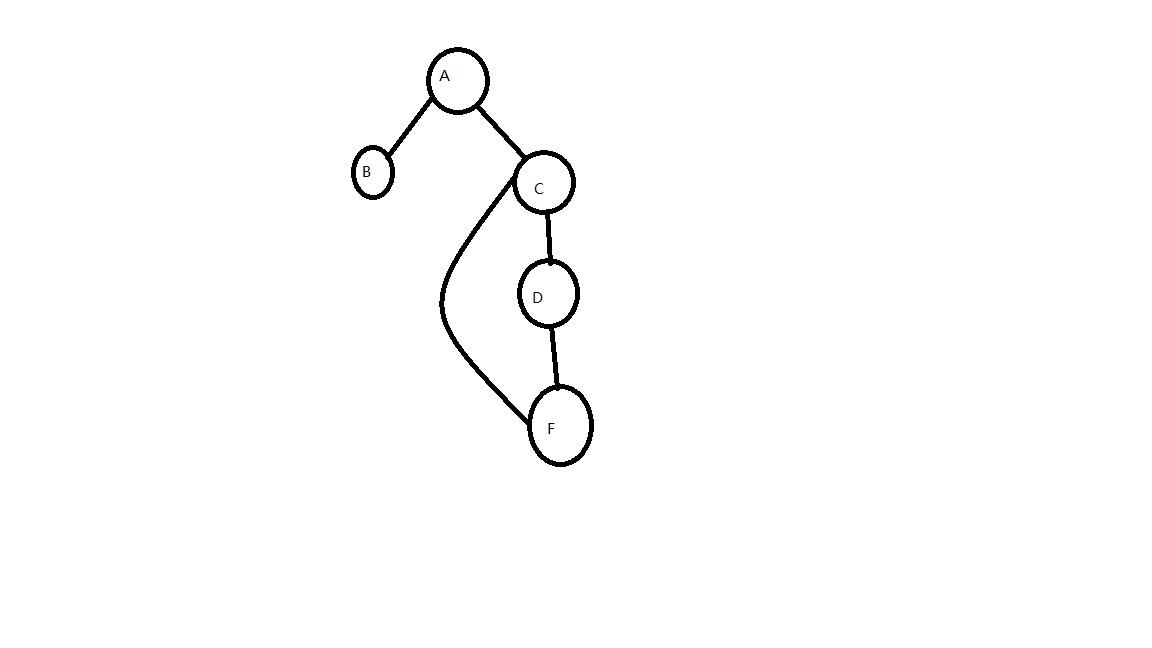
以dfs建立的一棵树(虽然并不是树)就能满足我们的要求,由此可以得到一条定理:在无向连通图G的DFS树中,非根节点u是G的割点当且仅当u存在一个子节点v,使得v及其后代都没有反向边连回u的祖先(连回u不算).
证明很简单,如果有边连回祖先,那么删除这个点后,剩下的点都能通过这条边组成一个连通分量,数目不变.
现在考虑怎么实现这个算法,设low(u)为u及其后代能连回的最早的祖先的pre值,pre值是我们认为规定的一个值,定义是dfs到节点u时,pre[u] = ++dfs_clock, dfs_clock是一个累加器,目的是为了记录到每个节点的时间.那么u是割点当且仅当low(v) >= pre(u),v是u的子节点.这时有一个特殊情况:v的后代只能连回v自己,即low(v) > pre(u),这个时候边(u,v)和(v,u)就是桥,具体的证明可以参考上面割点的证明.
算法的具体实现:
int dfs(int u, int fa) { int lowu = pre[u] = ++dfs_clock; int child = 0; for (int i = head[u]; i + 1; i = nextt[i]) { int v = to[i]; if (!pre[v]) { child++; int lowv = dfs(v, u); lowu = min(lowv, lowu); if (lowv >= pre[u]) //记录割顶 flag[u] = true; if (lowv > pre[u]) //记录桥 flag2[u][v] = flag2[v][u] = 1; } else if (pre[v] < pre[u] && v != fa) //千万不要漏掉第二个条件,这是(fa,u)的第二次访问,不是指向祖先的边! lowu = min(lowu, pre[v]); } if (fa < 0 && child == 1) //特判根节点 flag[u] = 0;return lowu; }
初始化的时候pre全部为0,开始dfs的时候fa = -1,基本上注意点都在代码里了,至于为什么我们遇到割点不直接输出是因为一个割点可能有多个子节点满足条件,防止重复输出.
以上是关于「学习笔记」双连通分量割点与桥的主要内容,如果未能解决你的问题,请参考以下文章

