急急急！求matlab图像求二值图像相似度，在线等！

Posted 2023-05-07

算法很简单，已知两个二值图像，逐一比较每个像素，相同的+1，不相同的+0。最后用这个数处以第一个图像的总像素数，最后得出相似度。我想得到但是不会编，求高手为我编一个完整程序。要完整的！

图像1和2为RGB图，放在m文件夹下；直接输入二值的话就不用im2bw了，pio是相似比

I1=imread('1.jpg');
I2=imread('2.jpg');
I1_bw=im2bw(I1);%%二值化
I2_bw=im2bw(I2);
[h,w]=size(I1_bw);%%获取图的宽高h/w
sum=0;
for i=1:h
for j=1:w

if I1_bw(i,j)==I2_bw(i,j)%%逐点比较相似
sum=sum+1;
end

end
end

pio=double(sum)/h/w; 参考技术A 你得把图像读出来呀，用imread命令试试吧。读出来以后你自己就会编了
例如先把当前目录改变到图像文件下，然后读入pic1=imread('X1.bmp');
pic2=imread('X2.bmp');X?.bmp改成对应的文件名。
矩阵可能是二维也可能是三维的，得到矩阵后应该就没什么问题了吧！ 参考技术B pic1=imread('D:\Notepad\matlab\图片生成avi\结果\1.bmp');
pic2=imread('D:\Notepad\matlab\图片生成avi\结果\2.bmp');
if any(size(pic1)-size(pic2))
error('两个图像的长宽不符')
end
picdiff=sum(pic1==pic2,3); %rgb的叠加
picdiff=picdiff==0; %相同的为1，不同为0。这里要求rgb全部相同才为1

sum(picdiff(:))/(size(pic1,1)*size(pic1,2)) 参考技术C 直接做个差分，然后求和。

求二值图像的最小外接矩形

算法描述

计算最小外接矩形（MER）的一种方法是，将物体的边界以每次以一定的角度增量（例如3°）在90°范围内旋转。每旋转一次记录一次其坐标系方向上的外接矩形边界点的最大和最小x、y值。旋转到某一个角度后，外接矩形的面积(或周长)达到最小。取面积最小的外接矩形的参数为主轴意义下的长度和宽度。

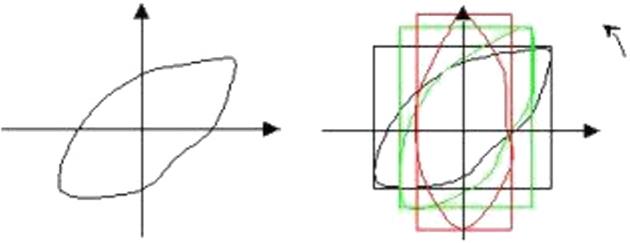
步骤流程

1. 输入图像
   

2. 输出图像
   旋转角度从0°~90°，步长为10°，求得的MER，如下图；
   
   旋转角度从0°~90°，步长为1°，求得的MER，如下图。
   

源代码

%%%寻找图像最小外接矩形

%%%先用迭代式阈值求法将图像变为二值图
img = imread('test0.png');
img = rgb2gray(img);
Th = mean(img( : ));            %将灰度均值设为初始阈值
newTh = 0;
i = 1;
while (Th - newTh) > 1
    pic1 = img;
    pic1(pic1 > Th) = 0;            %大于阈值置零方便求均值
    miu1 = mean(pic1(:));        %小于阈值的像素的灰度均值
    pic2 = img;
    pic2(pic2 < Th) = 0;            %小于阈值置零方便求均值 
    miu2 = mean(pic2( : ));      %大于阈值的像素的灰度均值
    if i ~= 1
        Th = newTh; 
    end
    i = i + 1;
    newTh = (miu1 + miu2) / 2;
end
imgTh = img;
imgTh(imgTh < Th) = 1;
imgTh(imgTh > Th) = 256;
imgTh = 256 - imgTh;
%%%先用迭代式阈值求法将图像变为二值图
%%%旋转图像求其MER
for angle = 0 : 1 : 90
    imgRotated = double(imrotate(imgTh,angle,'bicubic','loose'));  %求旋转后的图像
    %imshow(uint8(imgRotated));
    [row, col] = size(imgRotated);

    %%%判断最小外接矩形的边界
    for i = 1 : row
        if sum(imgRotated(i, :)) > col
            break;
        end
    end
    yMinTest = i;

    for i = row : -1 : 1
        if sum(imgRotated(i, :)) > col
            break;
        end
    end
    yMaxTest = i;

    for i = 1 : col
        if sum(imgRotated(:, i)) > row
            break;
        end
    end
    xMinTest = i;

    for i = col : -1 : 1
        if sum(imgRotated(:, i)) > row
            break;
        end
    end
    xMaxTest = i;
    %%%判断最小外接矩形的边界
    
    %%%计算面积
    XLU = xMinTest * cosd(angle) - yMinTest * sind(angle);
    YLU = xMinTest * sind(angle) + yMinTest * cosd(angle);

    XLD = xMinTest * cosd(angle) - yMaxTest * sind(angle);
    YLD = xMinTest * sind(angle) + yMaxTest * cosd(angle);

    XRU = xMaxTest * cosd(angle) - yMinTest * sind(angle);
    YRU = xMaxTest * sind(angle) + yMinTest * cosd(angle);

    XRD = xMaxTest * cosd(angle) - yMaxTest * sind(angle);
    YRD = xMaxTest * sind(angle) + yMaxTest * cosd(angle);
        
    l1 = sqrt((XLU - XRU) ^ 2 + (YLU - YRU) ^ 2);
    l2 = sqrt((XLU - XLD) ^ 2 + (YLU - YLD) ^ 2);


    nowSize = l1 * l2;
    %%%保存当前求得的MER
    if angle == 0 || nowSize < typicalSize
        xMin = xMinTest;
        yMin = yMinTest;
        xMax = xMaxTest;
        yMax = yMaxTest;
        typicalSize = nowSize;
        typicalAngle = angle;
        typicalImg = imgRotated;
    end
    %%%保存当前求得的MER
    lastSize = nowSize;
end

%%%重现
XLU = xMin * cosd(typicalAngle) - yMin * sind(typicalAngle);
YLU = xMin * sind(typicalAngle) + yMin * cosd(typicalAngle);

XLD = xMin * cosd(typicalAngle) - yMax * sind(typicalAngle);
YLD = xMin * sind(typicalAngle) + yMax * cosd(typicalAngle);

XRU = xMax * cosd(typicalAngle) - yMin * sind(typicalAngle);
YRU = xMax * sind(typicalAngle) + yMin * cosd(typicalAngle);

XRD = xMax * cosd(typicalAngle) - yMax * sind(typicalAngle);
YRD = xMax * sind(typicalAngle) + yMax * cosd(typicalAngle);
%%%重现

subplot(2,1,1);
imshow(uint8(imgTh));
title('原图像');

out1 = imrotate(imgTh,typicalAngle,'bicubic','loose');
rectx = [xMin, xMax, xMax, xMin, xMin];
recty = [yMax, yMax, yMin, yMin, yMax];
subplot(2,1,2);
imshow(out1);
title(['旋转角度为',num2str(typicalAngle),'°']);
line(rectx(:),recty(:),'color','r');

% out2 = imrotate(Figure1,-typicalAngle,'bicubic','loose');
% imshow(out2);
% rectx = [XLU, XLD, XRD, XRU, XLU];
% recty = [YLU, YLD, YRD, YRU, YLU];
% imshow(uint8(imgTh));
% line(rectx(:),recty(:),'color','r');
%%%旋转图像求其MER

结论

从输入输出图像中可以看到，通过旋转图像法求最小外接矩形，实验效果较好。通过改变旋转角度的步长可以使MER的计算变得更为精确，但也会使得程序运行时间增加。此外通过这一方法求MER，阈值分割的准确性也很重要，本次实验中选区的图像背景较为简洁，因此阈值分割效果也比较好。但在实际应用中，背景通常没有这么间接，因此在进行阈值分割时应当进行形态学的腐蚀与膨胀，以确保阈值分割的效果。一旦阈值分割出现一点点小瑕疵，整个程序都会出问题。

原始图像在旋转55°之后的坐标系内，有主轴意义下的MER。