echarts图表——盒须图&k线图
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了echarts图表——盒须图&k线图相关的知识,希望对你有一定的参考价值。
参考技术A 箱形图(Box-plot)又称为盒须图、盒式图或箱线图,是一种用作显示一组数据分散情况资料的统计图。因形状如箱子而得名。在各种领域也经常被使用,常见于品质管理。它主要用于反映原始数据分布的特征,还可以进行多组数据分布特征的比较。箱线图的绘制方法是:先找出一组数据的上边缘、下边缘、中位数和两个四分位数;然后, 连接两个四分位数画出箱体;再将上边缘和下边缘与箱体相连接,中位数在箱体中间。股市及期货市场中的K线图的画法包含四个数据,即开盘价、最高价、最低价、收盘价,所有的k线都是围绕这四个数据展开,反映大势的状况和价格信息。如果把每日的K线图放在一张纸上,就能得到日K线图,同样也可画出周K线图、月K线图。
利用箱线图过滤数据
箱线图
维基百科:
箱形图(英文:Box plot),又称为盒须图、盒式图、盒状图或箱线图,是一种用作显示一组数据分散情况资料的统计图。
因型状如箱子而得名。此图中之盒子之外,也常会有线条在上下四分位数之外延伸出去,像是胡须,因此也称为盒须图。离群值会有时会画成是个别的点。箱型图是无母数的,他显示样品的特性,对于母体分布并无任何假设。在各种领域也经常被使用,常见于品质管理。不过作法相对较繁琐。
箱形图于1977年由美国著名统计学家约翰·图基(John Tukey)发明。它能显示出一组数据的最大值、最小值、中位数、及上下四分位数。
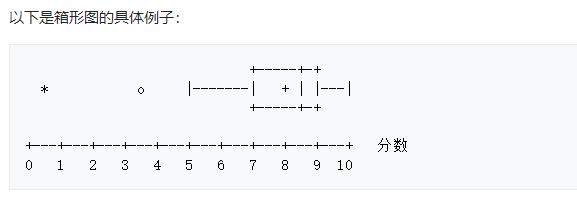
这组数据显示出:
- 最小值(minimum)=5
- 第一四分位数(Q1)=7
- 中位数(Med --也就是Q2)=8.5
- 第三四分位数(Q3)=9
- 最大值(maximum )=10
- 平均值=8
- 四分位间距(interquartile range)={\\displaystyle (Q3-Q1)}{\\displaystyle (Q3-Q1)}=2 (即ΔQ)
在区间 Q3+1.5ΔQ, Q1-1.5ΔQ 之外的值被视为应忽略(farout)。
- farout: 在图上不予显示,仅标注一个符号∇。
- 最大值区间: Q3+1.5ΔQ
- 最小值区间: Q1-1.5ΔQ
最大值与最小值产生于这个区间。区间外的值被视为outlier显示在图上.
- mild outlier(离群值) = 3.5
- extreme outlier (极端值) = 0.5
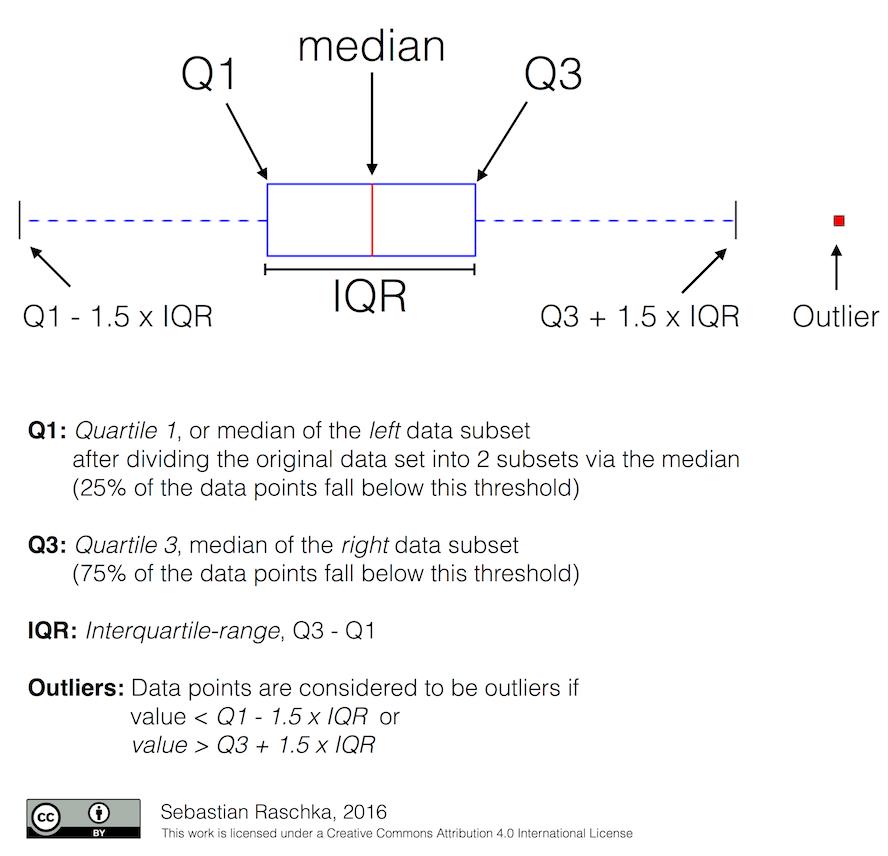
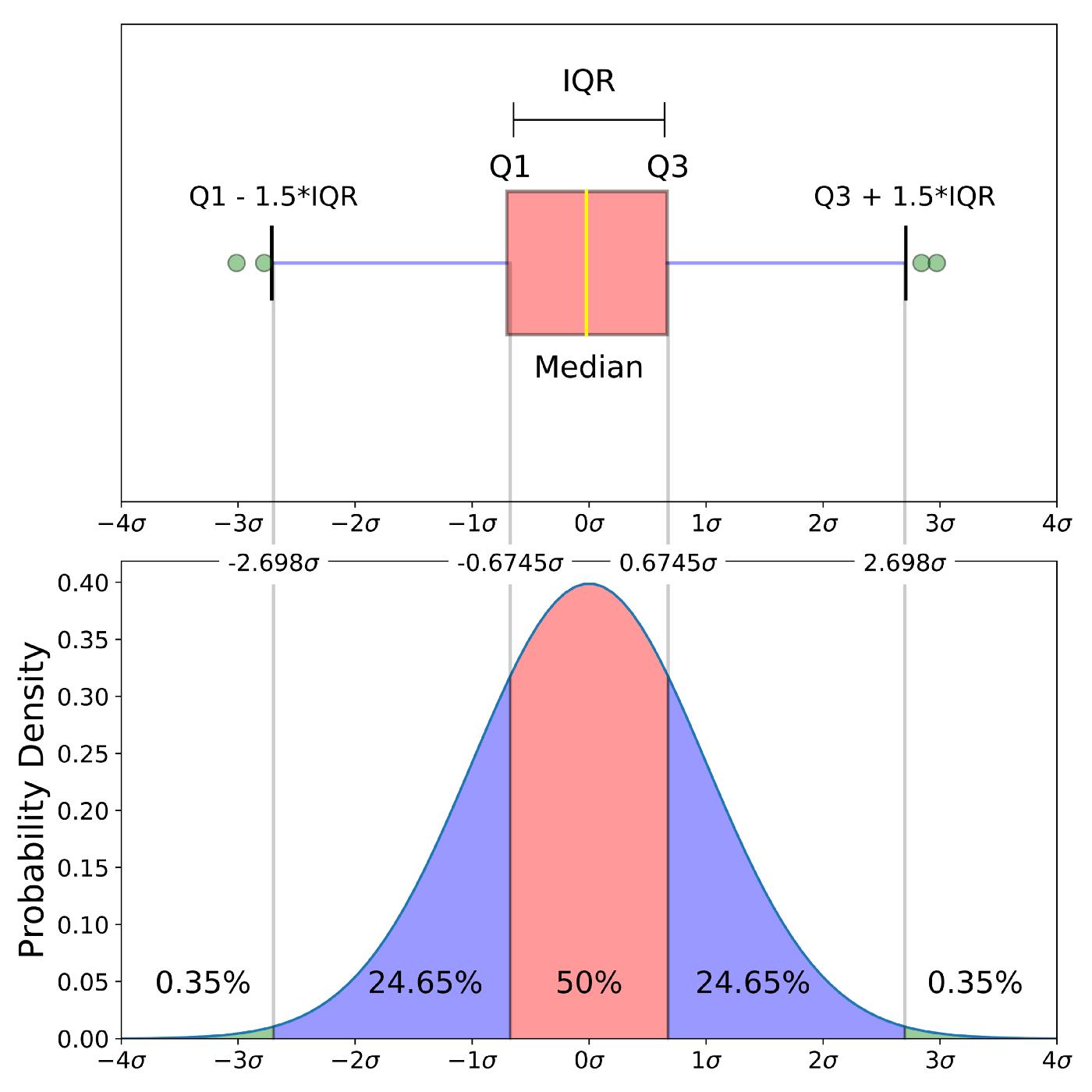
总之我们要知道的是,我们可以利用箱线图来处理一组数据中的异常数据
而这个数据处于箱线图的最大值以上,以及最小值以下!
箱线图分析和过滤数据
单组数据的箱线图绘制
利用matplotlib 库 pyplot 模块里的 boxplot() 函数
import matplotlib.pyplot as plt
# 生成数据
#x = pd.Series([1,2,3,3,4,5,10,12,2,2,3,1,4,3,-10,-1])同样可以使用series来绘制
x = [1,2,3,3,4,5,10,12,2,2,3,1,4,3,-10,-1]
plt.boxplot(x,patch_artist=True,labels=['test data'])
plt.show()
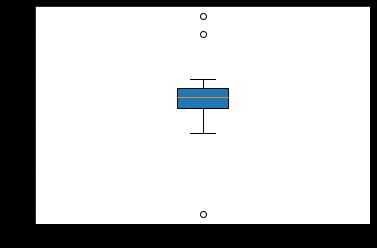
其中可选参数为
图片参考链接-百里希文

多组数据的箱线图绘制
多组数据的箱线图可以利用pandas中dataframe的boxplot方法
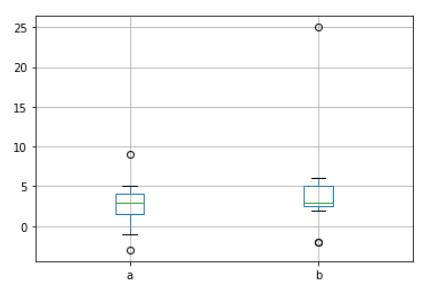
testData = pd.DataFrame({"a":[1,2,3,4,9,5,4,3,4,-1,-1-2],
"b":[2,3,3,3,4,5,5,6,25,-2,-2]})
testData.boxplot()
数据过滤
单组数据
对于单组数据的处理,我们可以通过查看图来进行数据的过滤;
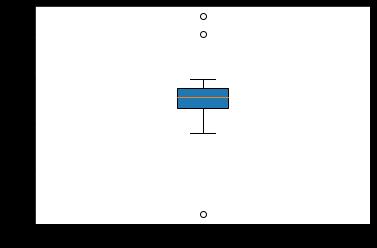
import matplotlib.pyplot as plt
x = pd.Series([1,2,3,3,4,5,10,12,2,2,3,1,4,3,-10,-1])
plt.boxplot(x,patch_artist=True,labels=['test data'])
plt.show()
这里我们可以看到数据为10和12以及-10是异常数据,因此我们将其剔除
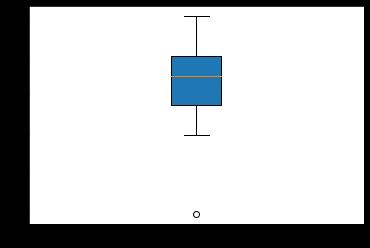
#将小于5,并且大于-5的数据保留
plt.boxplot(x[(x<5) & (x>-5)],patch_artist=True,labels=['test data'])
plt.show()
多组数据
当数据很多的时候,我们肉眼来进行查看显然是不现实的
比如以下图

那么我们如何进行数据异常的过滤呢?我们可以利用pandas中dataframe的boxplot方法返回的值进行数据过滤。通过设定return_type为dict我们就可以获取箱线图的每个组件映射到Line2D创建的实例列表的字典。
该字典具有以下键(假设垂直箱线图):
- boxes:箱线图的主体显示四分位数和中位数的置信区间(如果启用)。
- medians:每个框中间的水平线。
- whiskers:垂直线延伸到最极端的非异常数据点。
- caps:胡须末端的水平线。
- fliers:代表超出胡须(传单)的数据的点。
- means:代表均值的点或线。
这里我们需要的即为fliers的值,而这个fliers的获取值是一个列表,保存的是每一列(每个属性)的异常值的信息,该信息为matplotlib.lines.Line2D的类型,我们就可以获取异常点的相关信息
举个例子
testData = pd.DataFrame({"a":[1,2,3,4,9,5,4,3,4,-1,-1-2],
"b":[2,3,3,3,4,5,5,6,25,-2,-2]})
allbox = testData.boxplot(return_type='dict')
print(type(allbox["fliers"]))
print(type(allbox["fliers"][0]))
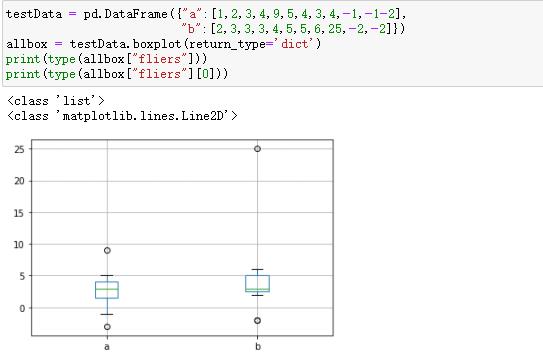
我们通过matplotlib.lines.Line2D中的 get_ydata来获取异常点的纵坐标
allbox["fliers"][0].get_ydata()
可以看到这里异常值为 -3以及9

从而我们可以通过判断数据的值来将数据剔除。
这里给出一个函数,将异常值剔除
def boxfilter(data, proportion:float):
allbox = data.boxplot(return_type='dict')
zipped = zip(allbox['fliers'], testData.columns)
i = 0
for flier, index_name in zipped:
# 获取一个列的异常y值
y = flier.get_ydata()
# 获取数据长度
datalenth = data.shape[0]
# 如果有异常值才处理
if(len(y) >= 1):
#对于每一个异常值做处理
for i in y:
#因为你不知道异常值是高于还是低于,因此这里做两次判断(异常值毕竟是少数)
#如果留下来的数据规模是大于以前数据规模*proportion的,则进行处理,这个取决于你来定
if(data[data[index_name] < i].shape[0] >=datalenth*proportion):
data = data[data[index_name] < i]
elif(data[data[index_name] > i].shape[0] >= datalenth*proportion):
data = data[data[index_name] > i]
return data
使用例子
def boxfilter(data, proportion:float):
allbox = data.boxplot(return_type='dict')
zipped = zip(allbox['fliers'], testData.columns)
i = 0
for flier, index_name in zipped:
# 获取一个列的异常y值
y = flier.get_ydata()
# 获取数据长度
datalenth = data.shape[0]
# 如果有异常值才处理
if(len(y) >= 1):
#对于每一个异常值做处理
for i in y:
#因为你不知道异常值是高于还是低于,因此这里做两次判断(异常值毕竟是少数)
#如果留下来的数据规模是大于以前数据规模*proportion的,则进行处理,这个取决于你来定
if(data[data[index_name] < i].shape[0] >=datalenth*proportion):
data = data[data[index_name] < i]
elif(data[data[index_name] > i].shape[0] >= datalenth*proportion):
data = data[data[index_name] > i]
return data
testData = pd.DataFrame({"a":[1,2,3,4,9,5,4,3,4,-1,-1-2],
"b":[2,3,3,3,4,5,5,6,25,-2,-2]})
newdata = boxfilter(testData,0.7)
newdata.boxplot(return_type='dict')
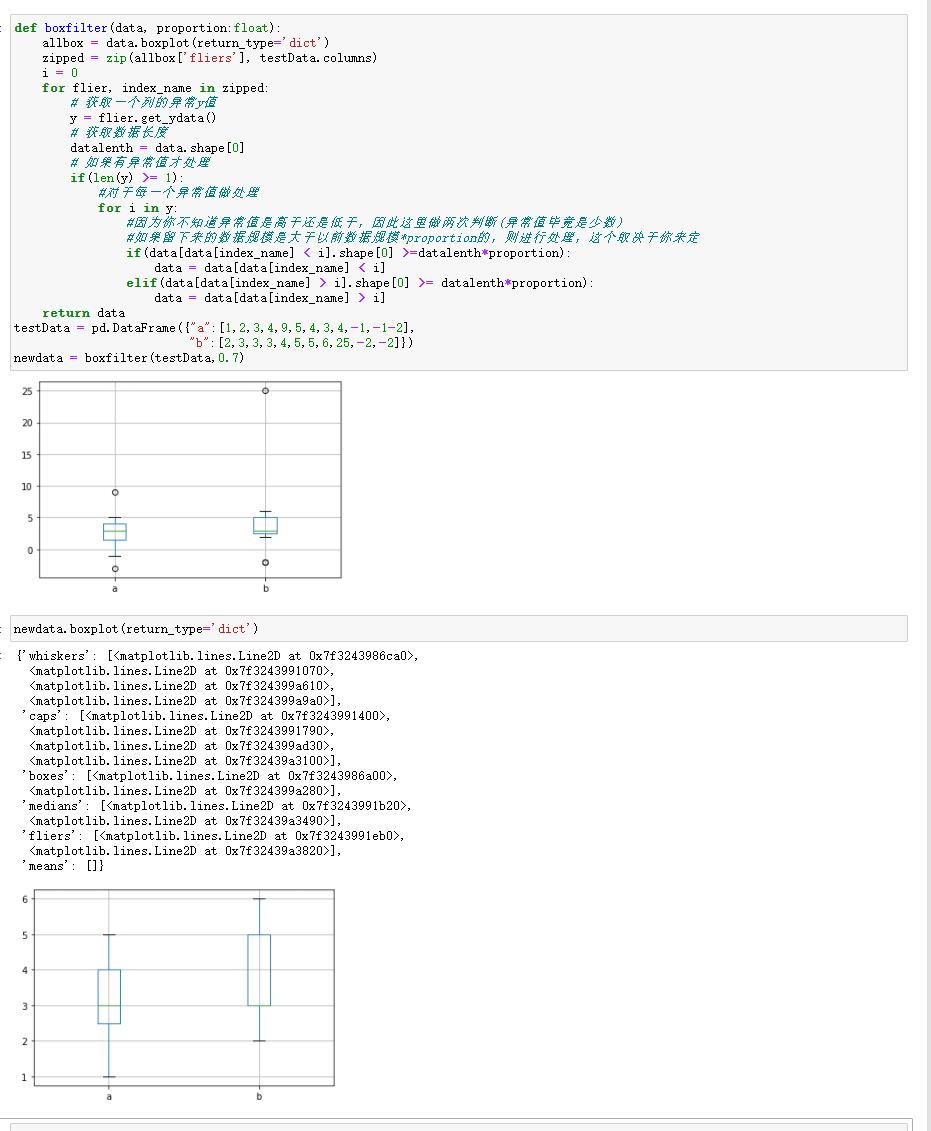
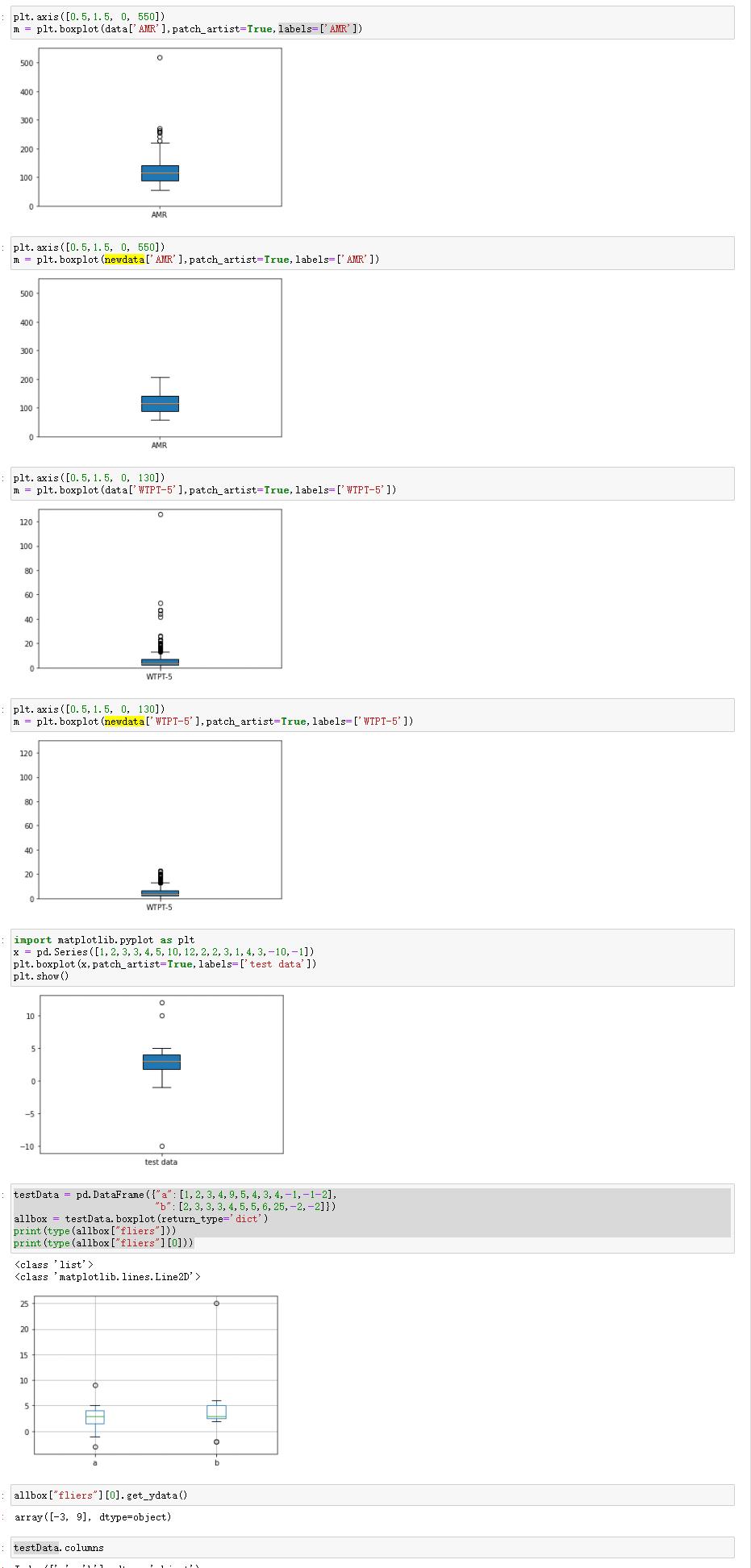
一些滤出图
以上是关于echarts图表——盒须图&k线图的主要内容,如果未能解决你的问题,请参考以下文章