python 求lna满足给定误差的值

Posted 2023-05-05

参考技术A

需要有特定的题才能求的哦。

拓展：

模型方差

模型的方差是模型在拟合不同的训练数据时性能的变化大小。它反映特定数据对模型的影响。

“方差指的是，用不同训练数据进行模型评估时，模型表现的变化程度。”

——《统计学习及其在R中的应用》2014年版，第34页

一个高方差的模型在训练数据集发生细小变化时预测结果会发生很大变化。相反，对于低方差的模型，训练数据发生或大或小的改变时，预测结果的变化都很小。

低方差：训练数据集的变化对于模型来说影响很小。

高方差：训练数据集的变化对于模型来说影响很大。

方差一定是正值。

不可约误差

整体而言，模型的误差包含可约误差和不可约误差。

模型误差 = 可约误差 + 不可约误差

可约误差是我们可以去优化的成分。在模型通过学习训练集后这一数值会下降，我们会努力让这一数值尽可能地接近于零。

不可约误差是我们无法从模型中剔除的误差，在任何模型中都不可能被去除。

这一误差源于不可控因素，例如观测中的统计噪声。

“……通常会称之为“不可约噪声”，且不能在建模过程中剔除。”

——《预测模型应用》2013年版，第97页

同样的，尽管我们能够把可约误差压缩到接近于零或者非常小的值，甚至有时能够等于零，但不可约误差依然会存在。这决定了模型性能的下限。

“有一点是我们是需要牢牢记住的，那就是不可约误差始终会作为我们对目标Y预测精确率的下限值，这个边界在实践中永远是未知的。”

——《统计学习及其在R中的应用》2014年版，第19页

这提醒我们任何模型都不是完美的。

偏差-方差的权衡

对于模型的表现来说，偏差和方差是有关联的。

理想情况下，我们希望一个模型能有低偏差和低方差，但是在实际操作中这是非常具有挑战性的。实际上这是机器学习建模的目标。

降低偏差很容易使方差升高。相反，降低方差也会使得偏差升高。

“这被称之为一种‘权衡’，因为一般的方法很容易得到极低的偏差和很高的方差……或很低的方差和很高的偏差……”

——《统计学习及其在R中的应用》2014年版，第36页

这种关系一般被称为“偏差与方差的权衡”。这是一个关于思考如何选择模型和调整模型的概念框架。

我们可以基于偏差和方差来选择模型。简单的模型，例如线性回归和逻辑回归，通常具有高偏差和低方差。而复杂的模型，例如随机森林，通常具有低偏差和高方差。

我们通常会基于模型的偏差和方差所造成的影响来调整模型。对于K-近邻算法来说，超参数k控制着模型的偏差-方差权衡。k取值较小，例如k=1，会得到低偏差高方差的结果。反之k取值较大，如k=21，导致高偏差和低方差。

高偏差和高方差都不一定是坏的，但他们有可能会导致不良的结果。

我们时常要对一组不同的模型和模型参数进行测试，从而在给定的数据集中得到最好的结果。一个高偏差的模型有可能会是过于保守的，出现欠拟合。相反的，一个高方差的模型可能会出现过拟合。

我们有可能会选择提高偏差或方差，来减少模型的整体误差。

计算圆周率（Python123）

计算圆周率

描述

根据下面的泰勒级数关系式，求圆周率的值，当最后一项的值小于给定阈值时结束。

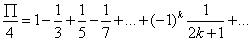
输入格式

输入在一行中给出小于1且大于0的阈值。

输出格式

在一行中输出满足阈值条件的近似圆周率，输出到小数点后6位。

代码

k = flag = 1
s = 0
epsilon = eval(input())
while 1 / (2 * k - 1) > epsilon:  # 当最后一项小于给定阈值时跳出循环
    s += 1 / (2 * k - 1) * flag  # 通过与flag相乘来实现加减交替
    flag = -flag  # 实现加减交替
    k += 1  # 将k加1
print(\'{:.6f}\'.format(4 * s))  # 前面的s是pi/4，需要乘4得到pi