基于原子范数的深度展开网络实现

Posted 2023-05-05 信

本文对现有的毫米波雷达-DOA估计方法进行了梳理，包括子空间分解、子空间你和、压缩感知（在网、离网和无网模型）；并重点对原子范数类压缩感知方法进行了实现和突破，主要突破点在于将原子范数理论和深度展开理论结合，解决了现有原子范数DOA估计求解的缺陷，旨在为线谱估计理论研究提供新的思路。

严肃声明

​ 严格禁止未经本人允许转载本文工作成果（包括引言、证明、代码分析等），一经发现被用于学术或商业用途，将予以法律警告。

引言

​ 毫米波雷达具有较高的中频带宽和多普勒带宽，这决定了其在距离和速度维的高分辨率特性，即目标相对雷达的空间距离与速度具有强确定性。然而，现阶段毫米波雷达多以小阵列孔径为主，因此限制了其角度分辨能力。为提升雷达的角分辨性能，现有的两种手段为虚拟孔径和超分辨·DOA估计·算法，增加虚拟孔径的方案有MIMO方式（通过TDM-MIMO以牺牲时间分辨为代价换取空间分辨）、自适应波形设计（对每个载波可以进行频率和相位的调制使每根接收天线在不同时间产生不同的相位，以虚拟出更多的接收天线）等。超分辨率算法则更偏向于后端信号处理，通过充分利用阵列接收信号或协方差矩阵中信息提升角度分辨性能。

​ DOA估计算法的起源最早可追溯到常规波束形成算法（Conventional Beamforming，CBF），这种算法将不同阵元接收到的信号视为不同间隔时间的采样数据，通过傅里叶变换将信号扩展到空域，实现空间谱估计。CBF方法容易受到瑞利极限的约束，无法分辨同处一个波束内的待测目标。为将时域非线性信号处理技术扩展到空间谱估计领域，谐波分析法、最小方差谱估计法、最大熵谱法被提出用于克服瑞利限的约束，但未充分利用阵元的二阶统计特性，难以满足实际工程需求。

​ 为突破瑞利极限约束，子空间方法被提出用改进空间信号估计性能，最典型的代表为由Schmidt等提出的多重信号分类方法（Multiple Signal Classification，MUSIC）和由Roy等提出的旋转子空间方法（Esitimating Signal Parameter via Rotation Invariance Techniques，ESPRIT），前者是基于信号子空间和噪声子空间的正交性先验，通过对搜索噪声子空间的零谱谱峰来估计信号在空间中的位置；后者是基于子阵列的信号子空间旋转不变性来求解旋转因子确定入射信号位置。实质上，这两种方法均基于严格的数据模型和协方差矩阵假设，具有较强的参数依赖性，对模型误差的容忍性有限，且对快拍数及信噪比、信号源相关性等外部条件要求较高。当参数假设不充分满足时，信号子空间和噪声子空间会发生能量泄露，即子空间正交性或旋转不变性不严格满足，因而影响角度估计性能。除了子空间分解以外，以最大似然方法（Deterministic maximum likelihood，DML）为代表的子空间拟合方法是另一种参数化模型的体现，这种方法通过对阵列流形矩阵和阵列接收信号子空间之间的最佳拟合实现对目标信号的估计，弥补了子空间分解方法在小快拍、低信噪比、相干源下的性能缺陷；然而，这种方法需要对目标信号来向进行联合搜索，计算复杂度较高，难以应用于实际的场景中。除此以外，子空间方法存在的共性问题是信源数目依赖性。

​ 随着信号理论的发展，Candes等提出了压缩感知理论，其打破了奈奎斯特采样定理中采样率的带宽限制条件，可使用较低的采样率实现有效信息的恢复，为DOA估计算法的设计打开了新思路。在DOA估计中，若将空域视为完备角度集，空间中不存在信号的角度对应的能量可视为零，只有少数项为非零值，那么目标入射信号相对整个空域范围是稀疏的，因此可以通过完备基中若干个原子的线性组合来表示目标信号，进而提取有用信息。通常，压缩感知重构算法可以等价为欠定方程组的求解问题，但由于解的稀疏性未知，该问题等价为基于\\(l_0\\)范数的NP-HARD问题。为解决NP-HARD问题，现前的研究主要基于信源与网格匹配假设分为在网（on-grid）、离网（off-grid）和无网格（gridless）等三类模型。

​ 在网模型是通过采样将空域角度离散化处理，并假设入射信号恰好落在网格上，然后扩展阵列接收模型得到的空域完备阵列接收模型。Mallat等利用完备集在信号稀疏重构中的特性，提出了匹配追踪算法，即"通过逐次迭代从完备集中选取基函数实现与前次残差信号最匹配的原子作为支撑，然后将上次残差减去其在已选支撑上的投影作为新的残差”，直至满足收敛。这种算法便于实现且计算量小，无需依赖噪声先验假设，但是分辨能力不足且收敛性无法保证。为改善匹配追踪类算法的缺陷，以\\(L_p\\)范数类凸优化问题为代表的的稀疏重构算法被提出，这类方法降低了信源数要求，在低信噪比、少快拍等信号环境具有较好的性能，典型的代表有\\(L_1-SVD\\)、\\(L_1-SRACV\\)（Sparse Representation of Array Covariance Vectors）、SPICE（Sparse Iterative Covariance-based Estimation）等。Malioutov提出的\\(L_1-SVD\\)方法从信号本身出发，通过构造包含波达角信息的过完备字典，将DOA估计问题转换为稀疏向量恢复问题，有效解决了单快拍和相干信号源下估计性能不足的问题，并且采用奇异值分解降低了多快拍数据矩阵求解的复杂度，但其全局极值解相对真实信号是有偏的。Yin等人提出的\\(L_1-SRACV\\)方法通过利用协方差矩阵中的信号方位和快拍能量信息,可实现更好的空间信号重构，但依赖于协方差矩阵的精确估计，即对快拍要求高。为降低快拍数对协方差矩阵的影响，Stoica等提出了SPICE方法，通过采用协方差拟合标准可得到近似真实协方差矩阵的估计值，进而实现DOA估计。除以上方法外，迭代自适应算法（Iterative Adaptive Approach，IAA）则是基于加权最小二乘法的非参自适应谱估计方法，通过最小化干扰和噪声的代价函数逐步迭代找到信号的稀疏表示，这种方法无需目标数目先验，在单快拍条件下亦可取得不错的估计性能。

​ 实际中，当目标入射信号偏离网格时会形成网格失配效应，进而影响高精度DOA估计性能。解决网格失配效应有两种思路：其一为增加网格采样密度，但这会导致计算复杂度的增加，并且加剧字典原子相关性以破坏有限等距性（Restricted Isometry Property，RIP）条件；其二为通过将网格参数化处理，和稀疏信号联合处理实现估计，即离网模型。离网模型主要可分为基于偏移量和基于动态网格这两类方法。偏移量模型是通过在阵列导向矢量引入一阶泰勒展开纠正项，以构建一阶偏移量和稀疏信号共同作为联合变量的估计模型，Yang等提出的OGSBI（Off-Grid Sparse Bayesian Inference）则是最经典的代表算法，能够有效地恢复各信号空域特征参数。动态网格方法则是通过在信号模型中引入网格变量后求解稀疏信号恢复问题。Austin等人提出了一种基于\\(L_1\\)范数的优化模型，这种方法可以实现求解非凸模型，但存在正则化参数的选取问题。Hu等则利用变分稀疏贝叶斯的思想对稀疏信号和网格进行了联合求解。

​ 尽管离网模型在一定程度上缓解了网格失配效应，但这引入了额外的网格变量，增加了模型的复杂度，并且在求解非凸优化过程中难以保证全局收敛；其本质上仍为网格模型，并且受到RIP限制。为了调和离散的网格点和系统模型连续的值域空间之间的矛盾，以协方差拟合标准和原子范数理论为代表的无网格方法提供了新的思路。Yang等基于SPICE中的协方差拟合标准提出了无网格SPICE（Gridless Spice，GLS）和稀疏参数方法（Sparse and Parametric Approach，SPA），这两者相互补充，SPA是GLS在多快拍场景中的扩展，这两种方法无需噪声功率和入射信号个数等先验，不涉及正则化参数，在小快拍下可实现渐近最大似然估计。Tang等提出了无噪声情况下基于半定规划（Semi-Definite Programming，SDP）的线谱估计和有噪声情况下采用原子范数软阈值法（Atomic Norm Soft Thresholding，AST）的线谱恢复方法，并验证了原子范数性能显著优于\\(L_1\\)范数。然而，基于无网格模型的需求求解SDP问题，计算复杂度较高，因此，交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）相比CVX工具箱而言能够提供更高的计算效率与全局收敛保障。

​ 总的来说，毫米波雷达的角度分辨性能受限于物理孔径，且现有的空间谱估计方法多依赖于大快拍、信噪比以及计算资源等限制，难以在真实场景中实现高精度的多目标方位估计与分辨。有鉴于此，本文旨在通过结合深度展开网络和基于ADMM优化的原子范数方法，将稀疏表示算法展开为一个以算法迭代次数为层数、算法参数为网络学习参数的神经网络，旨在克服无网格估计方法SDP求解的计算复杂度高、ADMM最优解易受参数初值选择影响等问题，实现单快拍下目标的鲁棒定位。

方法论

原子范数理论

​ 目标定位主要通过对雷达的天线维信号处理以恢复出真实目标在空间中的位置分布，为目标理解提供可靠的数据保证。现有的目标定位方法包括子空间分解、子空间拟合以及稀疏重构等，这些方法具有较强的可解释性与稳定性，但在小阵列孔径、单快拍和低信噪比等条件约束下的目标估计性能较差，并且计算复杂度较高；相较而言，以深度学习为主的目标定位方法则具有更快的推理和估计能力，但其可解释性较差。

​ 为结合传统理论模型和深度学习的优势，深度展开方法提供了新的解决思路。深度展开方法将特定的系数重构方法展开为深度神经网络，将算法的迭代次数作为层数，算法参数则作为网络的学习参数。现前，基于迭代软阈值的学习算法（Iterative Soft Thresholding Algorithm Based Learning，LISTA）实现了阵列缺陷下的快速DOA估计，迭代定点连续算法(Iterative Fixed-point Continuation, FPC)通过和深度神经网络结合实现了单比特DOA估计。诚然，通过有效地结合模型驱动与数据驱动的方法，与原有稀疏重构方法相比，深度展开方法能够大大降低计算复杂度，并实现更好的全局收敛、提升DOA估计性能。基于上述思想，本研究提出了基于无网格原子范数的深度展开方法，这种方法的底层原理基于交替方向投影算子优化的一阶原子范数理论，通过网络优化正则参数和惩罚因子，可有效解决参数初始化不合理造成的收敛和估计问题。

​ 在窄带信号模型中，设有M个阵元组成的均匀线性阵列接收K个远场窄带信号，那么阵列信号模型可以表示为：\\(y=x+n=A(θ)s+n\\)

​ 其中，\\(A(θ)=[a(θ_1 ),a(θ_2 ),…,a(θ_K)]\\)为阵列流形矩阵，\\(a(θ_k )=[1,e^-j2πdsinθ_k/λ,….,e^-j2π(M-1)dsinθ_k/λ]\\), \\(s\\)为入射信号，\\(n\\)为高斯白噪声信号。

​ 引入一个可描述连续参数空间的无限字典，即为原子集合A，那么该集合可以表述为\\(A=a(θ_k ):θ∈[-90,90]\\)。原子集合对应的凸包为conv(A)​，凸包关于原点中心对称，由原子集合A中的元素a构成，并且A中的任意元素不会处在除a以外的其他元素构成的凸包conv(A/a)中，即A的元素都是conv(A)的极值点。

​ 原子范数由凸包conv(A)的尺度函数定义，通过\\(‖·‖_A\\)表征。对单快拍信号x在凸包上的原子范数可以表示为:\\(\\left\\|x\\right\\|_A=\\inf\\limits_f_k,s_k\\t>0\\colon X\\in t\\textconv(A)\\\\)

​ 根据范德蒙分解定理，将\\(‖·‖_A\\)原子范数转化为等价的SDP形式为：\\(\\|x\\|_A=\\min\\frac12(t+u_1),s.t.\\beginbmatrixt&&x^H\\\\ x&&T(u)\\endbmatrix\\geq0\\)

​ 其中，\\(u_1\\)为\\(u\\)的第一个元素。

​ 在有噪声环境下，可以纠正无噪声原子范数表达式为如下目标函数：
\\(\\min\\limits_t,u\\|y-x\\|_2^2+\\tau\\|x\\|_A\\)
​ 其中，\\(‖·‖_2\\)表示向量的\\(L_2\\)范数，\\(\\tau\\)为正则化参数，其取值体现了不同项的权重。根据原子范数的定义，将有噪声问题转化为SDP问题，即：

​ \\(\\min\\limits_t,u\\frac12\\|y-x\\|_2^2+\\frac\\mathtt r2\\big(t+u_1\\big),s.t.\\beginbmatrixt&&x^H\\\\ x&&T(u)\\endbmatrix\\ge0\\)

​ 其中\\(T(u)\\in C^M\\times M\\)是托普利兹矩阵。

​ 如果考虑多快拍下的情况，那么对应的原子范数可以定义为\\(\\|X\\|_A_MMV=\\inf\\limits_f_k,\\mathcalx_k\\t>0\\colon X\\in tconv\\big(A_MMV\\big)\\\\)

​ 等价的半正定规划形式为:

​ \\(\\|X\\|_A_MMV=\\min\\limits_W,u\\frac12\\sqrtM\\big[tr(W)+tr\\big(T(u)\\big)\\big],s.t.\\beginbmatrixW&X^H\\\\ X&T(u)\\endbmatrix\\geq0\\)

​ 其中，tr(⋅)表示矩阵的迹。与之对应的DOA估计问题则可以表述为：\\(\\min\\limits_t,u\\frac12\\|Y-X\\|_F^2+\\eta\\|X\\|_A\\)

​ \\(‖N‖_F\\)表示矩阵的Frobenious范数，它的定义为\\(\\|N\\|_F=\\left(\\sum_i=1^m\\sum_j^n\\bigg|n_i,j\\bigg|^2\\right)^\\frac12\\)，至此，多快拍条件下原子范数最小化的优化问题可以转换为以下的SDP问题:\\(\\operatorname*min_t,u\\frac12\\|Y-X\\|_\\mathsfF^2+\\frac\\eta2\\sqrtM\\Big[t r(W)+t r\\Big(T(u)\\Big)\\Big],s.t.\\Big[\\beginmatrixT(u)&X\\\\ X^H&W\\endmatrix\\Big]\\geq0\\)

ADMM推导

​ 通过凸优化工具箱可以求解上述单快拍和多快拍原子范数的SDP问题的解\\(T(u)\\)，之后基于半正定托普利兹矩阵的范德蒙分解特性利用估计得到的矩阵\\(T(u)\\)实现DOA估计，或利用子空间方法实现DOA估计。考虑到凸优化工具包求解复杂度较高，可以采用交替方向乘子法ADMM求解，这种方法通过分解协调过程，将大的全局问题分解为多个较小、较容易求解的局部子问题，并通过协调子问题的解而得到大的全局问题的解，能够较好地保证算法的收敛性与减少算法的求解时间。在使用ADMM求解无网格DOA`估计问题时，以多快拍信号为例，求解流程可表述如下:

• 将优化问题重写为下述形式:\\(\\min\\limits_t,u\\frac12\\|Y-X\\|_F^2+\\frac\\tau2\\big(Tr(W)+Tr(u)\\big),s.t.Z=\\beginbmatrixT(u)&X\\\\ X^H&W\\endbmatrix,Z\\geq0.\\)

• 将上式重写为无约束条件下的增广拉格朗日函数形式，\\(\\Lambda\\)为拉格朗日乘子

  \\(L_\\rho=\\frac12\\|Y-X\\|_2^2+\\frac\\tau2(Tr(W)+Tr(u))+<A,\\Theta-\\beginbmatrixT(u)&X\\\\ X^H&W\\endbmatrix>+\\frac\\rho2\\|\\Theta-\\beginbmatrixT(u)&X\\\\ X^H&W\\endbmatrix\\Vert^2\\)

• 依次对各变量进行求导更新，步骤如下：

  \\((X^k+1,W^k+1,u^l+1)\\leftarrow\\textbfargmin_t,u,xL_\\rho(W,u,X,\\Theta^k,\\Lambda^k)\\)

  \\(\\Theta^k+1\\leftarrow\\mathbfargmin_Z\\geq0L_\\rho(W,u,X,\\Theta^k,\\Lambda^k)\\)

  \\(\\Lambda^k+1\\leftarrow\\Lambda^k+\\rho(\\Theta^k+1-\\left[\\beginmatrixT(u^k+1)&X^k+1\\cdot\\\\ (X^k+1)^H&W^k+1\\endmatrix\\right])\\)

  对变量\\(t，x，u\\)的更新过程表述如下：(可以参考范数经典问题的推导与分析，如果实在觉得困难不能够胜任矩阵形式的推导，在评论区或私信笔者会提供一份矩阵版本的推导。)

  \\(X^(k+1)=1/(1+2\\rho)(Y+2\\Lambda_X^(k)+2\\rho\\Theta_X^(k))\\)

  \\(W^k+1=\\Theta_W^(k)+\\frac\\Lambda_W^K-\\frac\\tau2I_L\\rho\\)

  \\(u^(k+1)=\\Gamma\\left(T^*\\left(\\Theta_T(u)^k+\\frac\\Lambda_T(u)\\rho\\right)-\\frac\\tau2\\rhoMe_1\\right),\\Gamma_ii=\\begincases\\frac1M,i=1\\\\ \\frac12(M-i+1),i>1\\endcases\\)

  其中，\\(Γ\\)为对角矩阵。

  \\(\\Theta^(k+1)=\\beginbmatrixT\\left(u^k+1\\right)&&X^k+1\\\\ (X^k+1)^H&&W^k+1\\endbmatrix-\\frac1\\rho\\Lambda^(k)\\)

  \\(\\Lambda^(k+1)=\\Lambda^(k)+\\rho(\\Theta^k+1-[\\beginmatrixT(u^k+1)&X^k+1\\\\ (X^k+1)^H&W^k+1])\\\\ \\endmatrix\\)

深度展开

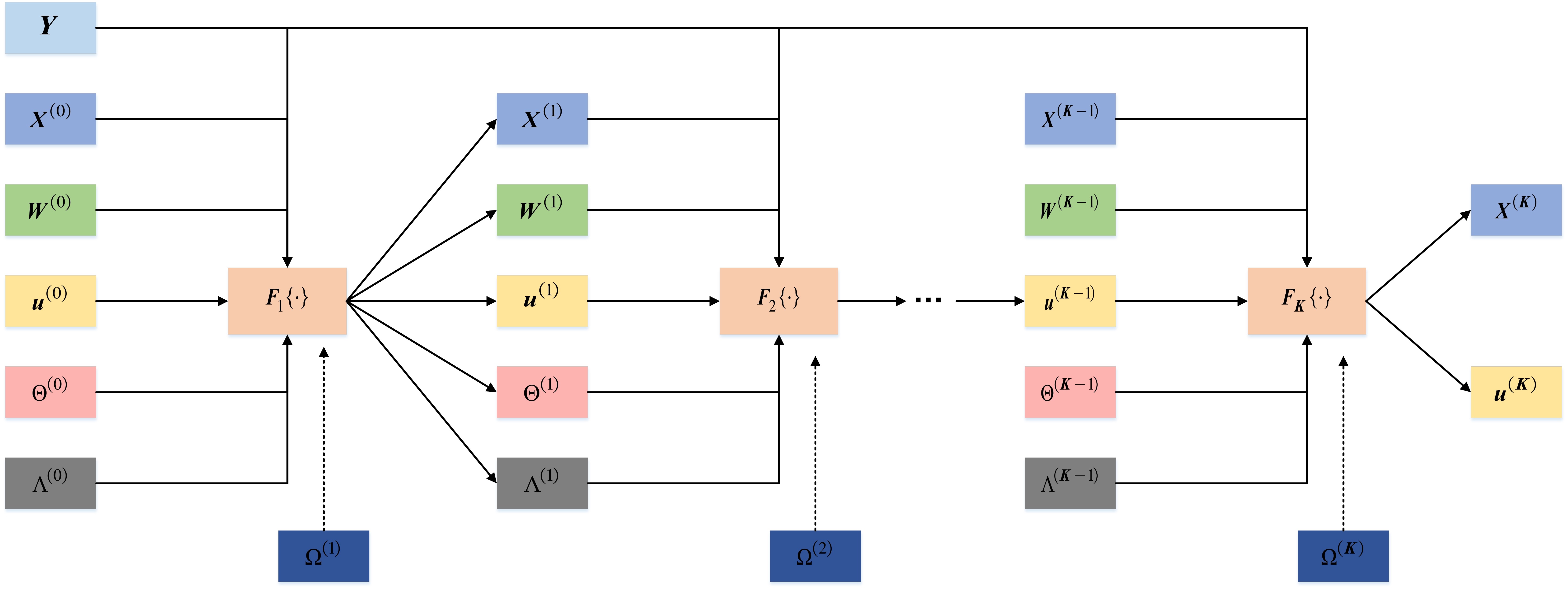
​ 根据上述推导，模型驱动ADMM算法的参数，包括惩罚因子\\(ρ\\)和正则化因子\\(\\tau\\)需要预先设置，这对实际应用是一个挑战。同时，不适当的参数设置会降低ADMM算法的收敛速度和精度，从而增加计算复杂度，降低DOA估计性能。即使可以通过理论分析和交叉验证方法选择合适的参数，固定的参数设置也不能保证ANM-ADMM算法的最优收敛。基于深度展开方法的思想，可以将该算法扩展为深度神经网络ANM-ADMM-Net，并从构造的服从特定分布的数据中学习其最优参数，以解决相关问题。

​ 将ANM-ADMM的K次迭代映射为实际的K层网络，输入信号为\\(Y,\\Theta^(0)=0_\\boldsymbolM\\times L,\\Lambda^(0)=0_\\boldsymbolM\\times L\\)，网络可学习参数为\\(\\Omega=\\left\\\\Omega^(k+1)\\right\\_k=0^K-1=\\left\\\\rho_k+1,\\tau_k+1,\\eta_k+1\\right\\_k=0^K-1\\)，\\(F_k+1\\\\cdot\\\\)包括了5个主要的结构子层，包括重构子层、辅助变量子层、托普利兹变换子层、非线性子层和乘法器子层，可表述如下:

​ 重构子层A：A层输出可以作为D和E的输入

​ \\(X^(k+1)=1/(1+2\\rho_k+1)(Y+2\\Lambda_X^(k)+2\\rho_k+1\\Theta_x^(k))\\)

​ 辅助变量子层B: (\\(τ_k+1\\)为可学习参数，B层输出可作为D和E的输入。

​ \\(W^(k+1)=\\rho_k+1^-1\\Lambda_W^(k)+\\Theta_W^(k)-\\tau_k+1/2\\rho_k+1I_L\\)

​ 托普利兹变换层C：C层输出可作为D和E的输入

​ \\(u^(k+1)=\\Gamma\\Bigg(T^*\\left(\\rho_k+1^-1\\Lambda_T(u)^(k)+\\Theta_T(u)^(k)-\\fracx_k+12\\rho_k+1M e_1\\right)\\Bigg).\\)

​ 非线性层D：

​ \\(\\Theta^(k+1)=\\beginbmatrixT(u^k+1)&X^k+1\\\\ (X^k+1)^H&W^k+1\\endbmatrix-\\rho_k+1^-1\\Lambda^(k)\\)

​ \\(\\Theta^(k+1)=Gdiag\\big(\\\\delta_g\\\\big)G^-1,\\Theta^(k+1)=Gdiag\\Big(\\\\delta_g\\_+\\Big)G^-1\\)

​ 乘法器更新子层E：

​ \\(\\Lambda^(k+1)=\\Lambda^(k)+\\eta_k+1(\\Theta^k+1-[\\beginmatrixT(u^k+1)&X^k+1\\\\ (X^k+1)^H&W^k+1])\\\\ \\endmatrix\\)

​ 如下图所示为所设计的深度展开网络

核心代码实现

下面给出MATLAB版本的ANM-ADMM核心程序和Python版本的深度展开网络核心程序[PS：笔者在这里挖了坑，防止某些人抱着拿来主义的心理~]

完整程序请见：链接：评论或私信笔者。

本文的思路是Python训练模型、获取学习参数表、在Matalb上进行推理测试。

function [X_new, T_new] = ADMM_ANM(Y, tau_list, rho_list, eta_list, iter)
    % 本程序针对多快拍下的原子范数ANM应用ADMM求解
    % 参考论文：Deep Unfolded Gridless DOA Estimation Networks Based on Atomic Norm Minimization
    % By Xuliang, 20230304
    % Y: 基带信号
    % tau: 正则参数
    % rho: 惩罚因子
    % iter: 迭代次数
    
    % 初始化变量 W X u Theta为0
    [M, L] = size(Y); % M 阵元 L 快拍
    
    Lam_old = zeros(M+L, M+L); % [LamT, LamX; LamXH, LamW] 
    The_old = zeros(M+L, M+L); %  LamT-M*M LamW-L*L LamX-M*L
    
    for id = 1 : iter
   
        % 最小化 X W Theta u
        X_new = (Y + Lam_old(1:M,M+1:end) +  Lam_old(M+1:end,1:M)\'  + rho_list(id) * The_old(1:M,M+1:end) + rho_list(id) * The_old(M+1:end,1:M)\') / (1 + 2 * rho_list(id)); % LamX TheX M*L
        W_new = 1 / rho_list(id) * Lam_old(M+1:end,M+1:end) + The_old(M+1:end,M+1:end) - tau_list(id) / (2*rho_list(id)) *eye(L); % LamW TheW
        
        normalizer = 1 ./ [M;((M-1):-1:1).\']; % 归一化系数
        e1 = zeros(M,1);e1(1)=1;
        u = 1 / rho_list(id) * normalizer .* (toeplitz_adjoint(Lam_old(1:M,1:M))...
                + rho_list(id) * toeplitz_adjoint(The_old(1:M, 1:M)) - tau_list(id) / 2 * M * e1);

        T_new = toeplitz(u);

        The_temp = [T_new, X_new; X_new\', W_new] - 1 / rho_list(id) * Lam_old; % 对其进行特征值分解
        [The_G, The_D] = eig(The_temp);
        diag_data = diag(The_D);
        data_idx = find(diag_data>0);
        The_new = The_G(:, data_idx) * diag(diag_data(data_idx)) * pinv(The_G(:, data_idx)); 
        The_new = (The_new + The_new\') / 2;
        Lam_new = Lam_old + eta_list(id) * (The_new - [T_new, X_new; X_new\', W_new]);
        
        % 更新
        Lam_old = Lam_new;
        The_old = The_new;
        
    end
    

class AnmNetwork(nn.Module):
    def __init__(self, K=10):
        super(AnmNetwork, self).__init__()

        self.RO = nn.ParameterList([nn.Parameter(torch.FloatTensor([1])) for i in range(K)])  # 惩罚因子
        self.TA = nn.ParameterList([nn.Parameter(torch.FloatTensor([1])) for i in range(K)])  # 正则参数
        self.ET = nn.ParameterList([nn.Parameter(torch.FloatTensor([1])) for i in range(K)])  # 控制Lamda的学习率
        self.max_iter = K  # 迭代次数
        
    def forward(self, Y):  # Y为输入信号 K为迭代次数
        batchs, M, L = Y.size(0), Y.size(1), Y.size(2)  # batch * M * snap
        Theta = torch.zeros(batchs, M + L, M + L, dtype=torch.complex128).to(device)
        Lamda = torch.zeros(batchs, M + L, M + L, dtype=torch.complex128).to(device)

        for i in range(self.max_iter):
            rho = self.RO[i]
            tau = self.TA[i]
            eta = self.ET[i]

            X_new = self.reconstruction_layer(Y, rho, Lamda, Theta, M, L)
            W_new = self.auxiliary_layer(rho, tau, Lamda, Theta, M)
            T_new = self.toeplitz_layer(rho, tau, Lamda, Theta, M)
            Theta = self.nonlinear_layer(rho, T_new, X_new, W_new, Lamda)
            Lamda = self.multiplier_layer(eta, T_new, X_new, W_new, Lamda, Theta)

        # 提取 u 向量
        uvec = torch.zeros((Lamda.size(0), 1, M), dtype=torch.complex128).to(device)

        for i in range(M):
            for j in range(i, M):
                uvec[:, 0, i] = uvec[:, 0, i] + T_new[:, j, j - i]
            uvec[:, 0, i] /= (M - i) * 1.
        # return spectrum
        uvec = uvec.squeeze(1)
        return T_new, uvec

参考文献

[1] 范数问题的经典推导, https://www.cnblogs.com/yuxuliang/p/MyNorm_1.html
[2] Zhu, H.; Feng, W.; Feng, C.; Ma, T.; Zou, B. Deep Unfolded Gridless DOA Estimation Networks Based on Atomic Norm Minimization. Remote Sens. 2023, 15, 13. https://doi.org/10.3390/rs15010013

[3] W. -G. Tang, H. Jiang and Q. Zhang, "Admm for Gridless Dod and Doa Estimation in Bistatic Mimo Radar Based on Decoupled Atomic Norm Minimization with One Snapshot," 2019 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Ottawa, ON, Canada, 2019, pp. 1-5, doi: 10.1109/GlobalSIP45357.2019.8969436.

范数的代数性质与解析性质

将学习到什么

范数的代数性质描述了构造新范数的方法，解析性质描述了两个不同的范数之间可能存在的关系.

?

---

代数性质

?
从给定的范数出发，可以用若干种方法构造出新的范数，比如两个范数的和是一个范数、一个范数的任意正的倍数还是范数、由已知两个范数取最大值构造的函数也是范数，这些结论全都是如下结果的特例.
?
??定理 1：设 \(\lVert \cdot \rVert _{\alpha_1}, \cdots, \lVert \cdot \rVert _{\alpha_m}\) 是域 \(\mathbf{F}\)（\(\mathbf{F}=\mathbb{R}\) 或者 \(\mathbb{C}\)）上的向量空间 \(V\) 上给定的范数，又令 $\lVert \cdot \rVert $ 是 \(\mathbb{R}^m\) 上一个满足 \(\lVert y \rVert \leqslant \lVert y+z \rVert\)（对所有非负元素的向量 \(y,z \in \mathbb{R}^m\)）的范数. 那么，由 \(f(x)=\lVert [ \lVert x \rVert_{\alpha_1},\cdots, \lVert x \rVert _{\alpha_m}]^T \rVert\) 所定义的函数 \(f\)：\(V \rightarrow \mathbb{R}\) 是 \(V\) 上的一个范数.
?
定理中关于范数 $\lVert \cdot \rVert $ 的单调性的假设是确保所构造的函数 \(f\) 满足三角不等式所需要的. 每一个 \(l_p\) 范数，就如同 \(\mathbb{R}^m\) 上仅仅是 \(x\) 的元素的绝对值的函数的任何一个范数 \(\lVert x \rVert_{\beta}\) 一样，都有这个单调性. 但是某些范数没有这个性质.
?

解析性质

?
在一个实的或者复的向量空间上许多不同的实值函数都能满足范数的公理，对某个给定的目的来说，一个范数有可能比另一个范数更方便或者更合适. 在实际应用中，可以建立起一套理论的范数与在一种给定的情形最容易计算的范数可能并不相同. 这样一来，重要的就是要知晓两个不同的范数之间可能存在的关系. 幸运的是，在有限维的情形下，所有范数在某种加强的意义下都是“等价的”.
?
分析中一个基本概念是序列的收敛性. 在赋范线性空间中，我们有如下的收敛性定义.
?
??定义 2：设 \(V\) 是有给定范数 $\lVert \cdot \rVert $ 的一个实的或者复的向量空间. 我们称 \(V\) 中一个向量序列 \(\{x^{(k)}\}\) 关于 $\lVert \cdot \rVert $ 收敛于一个向量 \(x \in V\)，当且仅当 \(\lim_{k \rightarrow \infty} \lVert x^{(k)} -x\rVert=0\). 如果 \(\{x^{(k)}\}\) 关于 $\lVert \cdot \rVert $ 收敛于 $x $，我们就写成关于 $\lVert \cdot \rVert $ 有 \(\lim_{k \rightarrow \infty}x^{(k)} =x\).
?
序列的极限如果存在，就是唯一的，也就是说向量序列不可能收敛于两个不同的极限. 一个向量序列有可能关于一个范数收敛，而关于另一个范数不收敛（这种情况在有限维赋范线性空间中不可能出现）.
?
??引理 3： 设 $\lVert \cdot \rVert $ 是域 \(\mathbf{F}\)（\(\mathbf{F}=\mathbb{R}\) 或者 \(\mathbb{C}\)）上的向量空间 \(V\) 上一个范数，\(m \geqslant 1\) 是一个给定的正整数，\(x^{(1)},x^{(2)},\cdots, x^{(m)} \in V\) 是给定的向量，又对任意的 \(z=[z_1 \cdots z_m]^T \in \mathbf{F}^m\) 定义 \(x(z) = z_1x^{(1)}+ z_2x^{(2)} + \cdots + z_mx^{(m)}\). 那么，由
\begin{align}
g(z) = \lVert x(z) \rVert = \lVert z_1x^{(1)}+ z_2x^{(2)} + \cdots + z_mx^{(m)} \rVert
\end{align}
所定义的函数 \(g\)：\(\mathbf{F}^m \rightarrow \mathbb{R}\) 就是 \(\mathbf{F}^m\) 上关于 Euclid 范数一致连续的函数.
?
上一个引理中的赋范线性空间 \(V\) 不一定是有限维的. 然而， \(V\) 的有限维度对于下面的基本结果是极其重要的.
?
??定理 4： 设 \(f_1\) 与 \(f_2\) 是域 \(\mathbf{F}\)（\(\mathbf{F}=\mathbb{R}\) 或者 \(\mathbb{C}\)）上一个有限维向量空间 \(V\) 上的实值函数，设 \(\mathscr{B}=\{x^{(1)},\cdots, x^{(n)}\}\) 是 \(V\) 的一组基，又设对所有 \(z=[z_1 \quad \cdots \quad z_n]^T \in \mathbf{F}^n\) 有 \(x(z) = z_1x^{(1)}+ z_2x^{(2)} + \cdots + z_nx^{(n)}\). 假设 \(f_1\) 与 \(f_2\) 是
??(a) 正的：对所有 \(x \in V\) 有 \(f_i(x) \geqslant 0\)，又设 \(f_i(x) = 0\) 当且仅当 \(x=0\)
??(b) 齐性的：对所有 \(\alpha \in \mathbf{F}\) 以及所有 \(x \in V\) 有 \(f_i(\alpha x) =\lvert \alpha \rvert f_i(x)\)
??(c) 连续的：\(f_1(x(z))\) 在 \(\mathbf{F}^n\) 上关于 Euclid 范数是连续的
那么就存在有限的正常数 \(C_m\) 以及 \(C_M\)，使得
\begin{align}
C_m f_1(x) \leqslant f_2(x) \leqslant C_Mf_1(x),\quad \text{对所有},, x \in V
\end{align}
如果一个有限维实的或者复的向量空间上的实值函数满足上述定理陈述的正性、齐性以及连续性这三个假设，它就称为一个准范数. 当然，准范数的最重要的例子是范数，引理 3 是说，每个范数都满足定理 4 中的连续性假设 (c). 满足三角不等式的准范数是范数.
?
??推论 5：设 \(\lVert \cdot \rVert _{\alpha}\) 以及 \(\lVert \cdot \rVert _{\beta}\) 是有限维实的或者复向量空间 \(V\) 上给定的范数. 那么就存在有限的正常数 \(C_m\) 与 \(C_M\)，使得对所有 \(x \in V\) 都有 \(C_m \lVert \cdot \rVert _{\alpha} \leqslant \lVert \cdot \rVert _{\beta} \leqslant C_M \lVert \cdot \rVert _{\alpha}\) .
?
推论 5 的一个重要的推论是如下事实：有限维复向量空间中向量序列的收敛性与所采用的范数无关.
?
??推论 6： 如果 \(\lVert \cdot \rVert _{\alpha}\) 以及 \(\lVert \cdot \rVert _{\beta}\) 是有限维实的或者复向量空间 \(V\) 上给定的范数. 又如果 \(x^{(k)}\) 是 \(V\) 中一列给定的向量，那么，关于 \(\lVert \cdot \rVert _{\alpha}\) 有 \(\lim_{k \rightarrow \infty}x^{(k)} =x\) 的充分必要条件是：关于 \(\lVert \cdot \rVert _{\beta}\) 有 \(\lim_{k \rightarrow \infty}x^{(k)} =x\).
?
??证明：由于对所有 \(k\) 都有 \(C_m \lVert x^{(k)}-x \rVert _{\alpha} \leqslant \lVert x^{(k)}-x \rVert _{\beta} \leqslant C_M \lVert x^{(k)}-x \rVert _{\alpha}\)，由此推出：当 $k \rightarrow \infty $ 时有 \(\lVert x^{(k)}-x \rVert _{\alpha} \rightarrow 0\) 成立的充分必要条件是当 $k \rightarrow \infty $ 时有 \(\lVert x^{(k)}-x \rVert _{\beta} \rightarrow 0\).
?
??定义 7： 实的或者复向量空间上两个给定的范数称为等价的，如果只要一个向量序列 \(x^{(k)}\) 关于其中一个范数收敛于一个向量 \(x\)，那么它就关于另一个范数也收敛于 \(x\)
?
推论 6 确保对有限维实或者复向量空间，所有的范数都是等价的. 对无限维向量空间来说，情况是非常不同的.
?
由于 \(\mathbb{R}^n\) 或 \(\mathbb{C}^n\) 上所有的范数都等价于 \(\lVert \cdot \rVert _{\infty}\)，对给定的一列向量 \(x^{(k)}=[x_i^k]_{i=1}^n\)，关于任何范数都有 \(\lim_{k \rightarrow \infty}x^{(k)} =x\) 的充分必要条件是：对每个 \(i=1,\cdots, n\) 都有 \(\lim_{k \rightarrow \infty}x_i^{(k)} =x_i\). 另一个重要事实是：单位球以及单位球面关于 \(\mathbb{R}^n\) 或 \(\mathbb{C}^n\) 上任意的准范数或者范数永远都是紧的. 由此，在这样一个单位球或者单位球面上的连续的实值或者复值函数都是有界的. 如果它是实值函数的话，它还取到它的最大以及最小值.
?
??推论 8：设 \(V=\mathbf{F}^n\)（\(\mathbf{F}=\mathbb{R}\) 或者 \(\mathbb{C}\)），并设 \(f(\cdot)\) 是 \(V\) 上的一个准范数或者范数. 那么集合 \(\{ x：f(x) \leqslant 1 \}\) 与 \(\{ x：f(x) = 1 \}\) 是紧集.
?
有时我们会遇到确定一个给定的序列 \(x^{(k)}\) 究竟是否收敛这样的问题. 为此，重要的是要有一个收敛的判别法，这个差别法里不明显含有该序列的极限（如果它存在的话）. 如果有这样的一个极限，那么，当 \(k,j \rightarrow \infty\) 时就有
\begin{align}
\lVert x^{(k)}-x^{(j)} \rVert = \lVert x^{(k)}-x+x-x^{(j)} \rVert \leqslant \lVert x^{(k)}-x \rVert + \lVert x-x^{(j)} \rVert \rightarrow 0
\end{align}
这就是下述定义之动因.
?
??定义 9： 向量空间 \(V\) 中一个序列 \(x^{(k)}\) 称为是关于范数 $\lVert \cdot \rVert $ 的一个 Cauchy 序列，如果对每个 \(\varepsilon >0\)，都存在一个正整数 \(N(\varepsilon)\)，使得只要 \(k_1,k_2 \geqslant N(\varepsilon)\) 就有 \(\lVert x^{(k_1)}-x^{(k_2)} \rVert \leqslant \varepsilon\).
?
??定理 10： 设 \(\lVert \cdot \rVert\) 是有限维实或者复向量空间 \(V\) 上的一个给定的范数，又设 \(x^{(k)}\) 是 \(V\) 中一个给定的向量序列. 序列 \(x^{(k)}\) 收敛于 \(V\) 中一个向量，当且仅当它关于范数 \(\lVert \cdot \rVert\) 是一个 Cauchy 序列.
?
一个序列是 Cauchy 序列，当且仅当它收敛于某个实的或者复的纯量. 这个结论是实数域或者复数域的一个基本性质. 这个性质称为实数域以及复数域的完备性. 我们刚刚证明了：完备性可以延拓到关于任何范数的有限维实或者复向量空间. 不幸的是，无限维赋范线性空间可能没有完备性.
?
??定义 11：一个赋范线性空间 \(V\) 称为关于它的范数 \(\lVert \cdot \rVert\) 是完备的，如果 \(V\) 中每一个关于 \(\lVert \cdot \rVert\) 是 Cauchy 序列的序列都收敛于 \(V\) 的一个点.
?

对偶范数

?
利用 \(\mathbb{R}^n\) 或者 \(\mathbb{C}^n\) 上任何范数或者准范数的单位球都是紧集这一事实，我们可以引进另外一个有用的方法，此外可以利用 Euclid 内积从老的范数生成新的范数.
?
??定义 12： 设 \(f(\cdot)\) 是 \(V=\mathbf{F}^n\)（\(\mathbf{F}=\mathbb{R}\) 或者 \(\mathbb{C}\)）上的一个准范数. 那么函数
\begin{align}
f^D(y) = \max\limits_{f(x)=1} \mathrm{Re} \langle x, y \rangle = \max\limits_ {f(x)=1} \mathrm{Re} \,\,y^*x
\end{align}
称为 \(f\) 的对偶范数.
?
对偶范数是 \(V\) 上一个具有良好定义的函数，因为对每个固定的 \(y \in V\)，$ \mathrm{Re} ,,y^*x$ 都是 \(x\) 的连续函数，且集合 \(\{x：f(x)=1\}\) 是紧的. Weierstrass 定理确保 $ \mathrm{Re} ,,y^*x$ 的最大值能在这个集合中的某个点取到. 对偶范数的一种等价的、有时用起来方便的另一种表达方式是
\begin{align}
f^D(y) = \max\limits_{f(x)=1} \lvert y^*x \rvert = \max\limits_{x \neq 0} \frac{\lvert y^*x \rvert}{f(x)}
\end{align}
函数 \(f^D(\cdot)\) 显然是齐次的. 值得注意的是，即使 \(f(\cdot)\) 不服从三角不等式，\(f^D(\cdot)\) 也总是服从的. 准范数的对偶范数是正的、齐次的，且满足三角不等式，所以它是一个范数. 特别地，范数的对偶范数恒为一个范数. 下面的引理中给出对偶范数的一个简单的不等式，它是 Cauchy-Schwarz 不等式的一个自然的推广.
?
??引理 13： 设 \(f(\cdot)\) 是 \(V=\mathbf{F}^n\)（\(\mathbf{F}=\mathbb{R}\) 或者 \(\mathbb{C}\)）上的一个准范数. 那么对所有 \(x,y \in V\) 我们有
\begin{align}
\lvert y^*x \rvert \leqslant f(x)f^D(y)
\end{align}
以及
\begin{align}
\lvert y^*x \rvert \leqslant f^D(x)f(y)
\end{align}
?
??证明：如果 \(x\neq 0\)，那么
\begin{align}
\lvert y^* \frac{x}{f(x)} \rvert \leqslant \max\limits_{f(x)=1} \lvert y^*x \rvert = f^D(y)
\end{align}
从而 \(\lvert y^*x \rvert \leqslant f(x)f^D(y)\). 当然，这个不等式对 \(x=0\) 也成立. 第二个不等式由第一个推出，这是因为 \(\lvert y^*x \rvert = \lvert x^*y\rvert\).
?
辨认出与某些熟悉的范数对偶的范数是有益的. 例如
\begin{align}
\lVert \cdot \rVert _1^D = \lVert \cdot \rVert_{\infty}, \quad \lVert \cdot \rVert_{\infty}^D=\lVert \cdot \rVert_1,\quad \lVert \cdot \rVert_2^D = \lVert \cdot \rVert_2
\end{align}
与
\begin{align}
\lVert \cdot \rVert_p^D = \lVert \cdot \rVert_q, \quad \text{其中}\,\, \frac{1}{p} + \frac{1}{q}=1, \quad p \geqslant 1
\end{align}
??引理 14： 设 \(f(\cdot)\) 与 \(g(\cdot)\) 是 \(V=\mathbf{F}^n\)（\(\mathbf{F}=\mathbb{R}\) 或者 \(\mathbb{C}\)）上的准范数，又设给定 \(c >0\). 那么
??(a) \(cf(\cdot)\) 是 \(V\) 上的准范数，且它的对偶范数是 \(c^{-1}f^D(\cdot)\)；
??(b) 如果对所有 \(x\in V\) 都有 \(f(x) \leqslant g(x)\)，那么对所有 \(y \in V\) 都有 \(f^D(y) \geqslant g^D(y)\).
?
??定理 15： 设 \(f(\cdot)\) 与 \(g(\cdot)\) 是 \(V=\mathbf{F}^n\)（\(\mathbf{F}=\mathbb{R}\) 或者 \(\mathbb{C}\)）上的范数，又设给定 \(c>0\). 那么对所有 \(x\in V\) 都有 \(\lVert x \rVert = c\lVert x \rVert ^D\) 成立的充分必要条件是 \(\lVert \cdot \rVert = \sqrt{c}\lVert x \rVert _2\). 特别地，\(\lVert \cdot \rVert = \lVert x \rVert ^D\) 成立的充分必要条件是 \(\lVert x \rVert = \lVert x \rVert _2\).
?
\(\mathbb{R}^n\) 或者 \(\mathbb{C}^n\) 上的每一个 \(k\) 范数以及每一个 \(l_p\) 范数都具有如下的性质：向量的范数仅与其元素的绝对值有关且还是 \(x\) 的元素的绝对值的非减函数. 这两个性质并非是不相干的.
?
??定义 16： 如果 \(x=[x_i] \in V=\mathbf{F}^n\)（\(\mathbf{F}=\mathbb{R}\) 或者 \(\mathbb{C}\)），设 \(\lvert x \rvert = [\lvert x_i \rvert]\) 表示 \(x\) 逐个元素的绝对值. 我们说 \(\lvert x \rvert \leqslant \lvert y \rvert\)，如果对所有 \(i=1,\cdots,n\) 都有 \(\lvert x_i \rvert \leqslant \lvert y_i \rvert\). \(V\) 上的范数称为是
??(a)单调的，如果 \(\lvert x \rvert \leqslant \lvert y \rvert\) 蕴含对所有 \(x,y \in V\) 都有 \(\lVert x \rVert \leqslant \lVert y \rVert\)；
??(b)绝对的，如果对所有 \(x \in V\) 都有 \(\lVert x \rVert = \lVert \lvert x \rvert \rVert\).
?
??定理 17：设 \(\lVert \cdot \rVert\) 是 \(V=\mathbf{F}^n\)（\(\mathbf{F}=\mathbb{R}\) 或者 \(\mathbb{C}\)）上一个范数.
??(a) 如果 \(\lVert \cdot \rVert\) 是绝对的，那么对所有 \(y \in V\) 都有
\begin{align}
\lVert y \rVert ^D = \max\limits_{x \neq 0} \frac{\lvert y \rvert ^T \lvert x \rvert}{\lVert x \rVert}
\end{align}
??(b) 如果 \(\lVert \cdot \rVert\) 是绝对的，那么 \(\lVert \cdot \rVert^D\) 是绝对的且是单调的.
??(c) 范数 \(\lVert \cdot \rVert\) 是绝对的，当且仅当它是单调的.
?

---

应该知道什么

• 从给定的范数出发，可以用若干种方法构造出新的范数
• 在有限维的情形下，所有范数在某种加强的意义下都是等价的