基于Python的模拟退火算法SA 以函数极值+TSP问题为例（gif动态展示）

Posted 2020-12-17 WA自动机~

算法流程：

 

 

 

 

 

 实现：

base.py

from abc import ABCMeta, abstractmethod
import types


class SkoBase(metaclass=ABCMeta):
    def register(self, operator_name, operator, *args, **kwargs):
        \'\'\'
        regeister udf to the class
        :param operator_name: string
        :param operator: a function, operator itself
        :param args: arg of operator
        :param kwargs: kwargs of operator
        :return:
        \'\'\'

        def operator_wapper(*wrapper_args):
            return operator(*(wrapper_args + args), **kwargs)

        setattr(self, operator_name, types.MethodType(operator_wapper, self))
        return self

# 空函数
class Problem(object):
    pass

sko目录下的operaters目录 mutation.py 用于TSP问题的状态空间转移函数的设计

import numpy as np


def mutation(self):
    \'\'\'
    mutation of 0/1 type chromosome
    faster than `self.Chrom = (mask + self.Chrom) % 2`
    :param self:
    :return:
    \'\'\'
    #
    mask = (np.random.rand(self.size_pop, self.len_chrom) < self.prob_mut)
    self.Chrom ^= mask
    return self.Chrom


def mutation_TSP_1(self):
    \'\'\'
    every gene in every chromosome mutate
    :param self:
    :return:
    \'\'\'
    for i in range(self.size_pop):
        for j in range(self.n_dim):
            if np.random.rand() < self.prob_mut:
                n = np.random.randint(0, self.len_chrom, 1)
                self.Chrom[i, j], self.Chrom[i, n] = self.Chrom[i, n], self.Chrom[i, j]
    return self.Chrom


# 交换两个点
def swap(individual):
    n1, n2 = np.random.randint(0, individual.shape[0] - 1, 2)
    if n1 >= n2:
        n1, n2 = n2, n1 + 1
    individual[n1], individual[n2] = individual[n2], individual[n1]
    return individual

# 逆转序列中指定的一段
def reverse(individual):
    \'\'\'
    Reverse n1 to n2
    Also called `2-Opt`: removes two random edges, reconnecting them so they cross
    Karan Bhatia, "Genetic Algorithms and the Traveling Salesman Problem", 1994
    https://pdfs.semanticscholar.org/c5dd/3d8e97202f07f2e337a791c3bf81cd0bbb13.pdf
    \'\'\'
    n1, n2 = np.random.randint(0, individual.shape[0] - 1, 2)
    if n1 >= n2:
        n1, n2 = n2, n1 + 1
    individual[n1:n2] = individual[n1:n2][::-1]
    return individual

# 分段交叉
def transpose(individual):
    # randomly generate n1 < n2 < n3. Notice: not equal
    n1, n2, n3 = sorted(np.random.randint(0, individual.shape[0] - 2, 3))
    n2 += 1
    n3 += 2
    slice1, slice2, slice3, slice4 = individual[0:n1], individual[n1:n2], individual[n2:n3 + 1], individual[n3 + 1:]
    individual = np.concatenate([slice1, slice3, slice2, slice4])
    return individual


def mutation_reverse(self):
    \'\'\'
    Reverse
    :param self:
    :return:
    \'\'\'
    for i in range(self.size_pop):
        if np.random.rand() < self.prob_mut:
            self.Chrom[i] = reverse(self.Chrom[i])
    return self.Chrom


def mutation_swap(self):
    for i in range(self.size_pop):
        if np.random.rand() < self.prob_mut:
            self.Chrom[i] = swap(self.Chrom[i])
    return self.Chrom

SA.py 定义了众多的模拟退火方案

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Time    : 2019/8/17
# @Author  : github.com/guofei9987

import numpy as np
from base import SkoBase
from sko.operators import mutation


class SimulatedAnnealingBase(SkoBase):
    """
    DO SA(Simulated Annealing)

    Parameters
    ----------------
    func : function
        The func you want to do optimal
    n_dim : int
        number of variables of func
    x0 : array, shape is n_dim
        initial solution
    T_max :float
        initial temperature
    T_min : float
        end temperature
    L : int
        num of iteration under every temperature（Long of Chain）

    Attributes
    ----------------------


    Examples
    -------------
    See https://github.com/guofei9987/scikit-opt/blob/master/examples/demo_sa.py
    """
#L是单次迭代中马尔科夫链的长度
    def __init__(self, func, x0, T_max=100, T_min=1e-7, L=300, max_stay_counter=150, **kwargs):
        assert T_max > T_min > 0, \'T_max > T_min > 0\'

        self.func = func
        self.T_max = T_max  # initial temperature
        self.T_min = T_min  # end temperature
        self.L = int(L)  # num of iteration under every temperature（also called Long of Chain）
        self.max_stay_counter = max_stay_counter  # stop if best_y stay unchanged over max_stay_counter times

        self.n_dims = len(x0)

        self.best_x = np.array(x0)  # initial solution
        self.best_y = self.func(self.best_x)
        self.T = self.T_max
        self.iter_cycle = 0
        self.best_y_history = [self.best_y]
        self.best_x_history = [self.best_x]

    def get_new_x(self, x):
        u = np.random.uniform(-1, 1, size=self.n_dims)#产生[-1,1]之间的随机数，维数指定
        x_new = x + 20 * np.sign(u) * self.T * ((1 + 1.0 / self.T) ** np.abs(u) - 1.0)
        return x_new

    def cool_down(self):
        self.T = self.T * 0.7

    def isclose(self, a, b, rel_tol=1e-09, abs_tol=1e-30):
        return abs(a - b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol)

    def run(self):
        x_current, y_current = self.best_x, self.best_y
        stay_counter = 0
        while True:
            for i in range(self.L):
                x_new = self.get_new_x(x_current)
                y_new = self.func(x_new)

                # Metropolis
                df = y_new - y_current
                if df < 0 or np.exp(-df / self.T) > np.random.rand():
                    x_current, y_current = x_new, y_new
                    if y_new < self.best_y:
                        self.best_x, self.best_y = x_new, y_new

            self.iter_cycle += 1
            self.cool_down()
            self.best_y_history.append(self.best_y)
            self.best_x_history.append(self.best_x)

            # if best_y stay for max_stay_counter times, stop iteration
            # 最后一次的best_y值和倒数第二次的best_y值一样，表示停留在平坦的状态
            if self.isclose(self.best_y_history[-1], self.best_y_history[-2]):
                stay_counter += 1
            else:
                stay_counter = 0

            if self.T < self.T_min:
                stop_code = \'Cooled to final temperature\'
                break
            if stay_counter > self.max_stay_counter:
                stop_code = \'Stay unchanged in the last {stay_counter} iterations\'.format(stay_counter=stay_counter)
                break

        return self.best_x, self.best_y

    fit = run


class SAFast(SimulatedAnnealingBase):
    \'\'\'
    u ~ Uniform(0, 1, size = d)
    y = sgn(u - 0.5) * T * ((1 + 1/T)**abs(2*u - 1) - 1.0)

    xc = y * (upper - lower)
    x_new = x_old + xc

    c = n * exp(-n * quench)
    T_new = T0 * exp(-c * k**quench)
    \'\'\'

    def __init__(self, func, x0, T_max=100, T_min=1e-7, L=300, max_stay_counter=150, **kwargs):
        super().__init__(func, x0, T_max, T_min, L, max_stay_counter, **kwargs)
        self.m, self.n, self.quench = kwargs.get(\'m\', 1), kwargs.get(\'n\', 1), kwargs.get(\'quench\', 1)
        self.lower, self.upper = kwargs.get(\'lower\', -10), kwargs.get(\'upper\', 10)
        self.c = self.m * np.exp(-self.n * self.quench)

    def get_new_x(self, x):
        r = np.random.uniform(-1, 1, size=self.n_dims)
        xc = np.sign(r) * self.T * ((1 + 1.0 / self.T) ** np.abs(r) - 1.0)
        x_new = x + xc * (self.upper - self.lower)
        return x_new

    def cool_down(self):
        self.T = self.T_max * np.exp(-self.c * self.iter_cycle ** self.quench)


class SABoltzmann(SimulatedAnnealingBase):
    \'\'\'
    std = minimum(sqrt(T) * ones(d), (upper - lower) / (3*learn_rate))
    y ~ Normal(0, std, size = d)
    x_new = x_old + learn_rate * y

    T_new = T0 / log(1 + k)
    \'\'\'

    def __init__(self, func, x0, T_max=100, T_min=1e-7, L=300, max_stay_counter=150, **kwargs):
        super().__init__(func, x0, T_max, T_min, L, max_stay_counter, **kwargs)
        self.lower, self.upper = kwargs.get(\'lower\', -10), kwargs.get(\'upper\', 10)
        self.learn_rate = kwargs.get(\'learn_rate\', 0.5)

    def get_new_x(self, x):
        std = min(np.sqrt(self.T), (self.upper - self.lower) / 3.0 / self.learn_rate) * np.ones(self.n_dims)
        xc = np.random.normal(0, 1.0, size=self.n_dims)
        x_new = x + xc * std * self.learn_rate
        return x_new

    def cool_down(self):
        self.T = self.T_max / np.log(self.iter_cycle + 1.0)


class SACauchy(SimulatedAnnealingBase):
    \'\'\'
    u ~ Uniform(-pi/2, pi/2, size=d)
    xc = learn_rate * T * tan(u)
    x_new = x_old + xc

    T_new = T0 / (1 + k)
    \'\'\'

    def __init__(self, func, x0, T_max=100, T_min=1e-7, L=300, max_stay_counter=150, **kwargs):
        super().__init__(func, x0, T_max, T_min, L, max_stay_counter, **kwargs)
        self.learn_rate = kwargs.get(\'learn_rate\', 0.5)

    def get_new_x(self, x):
        u = np.random.uniform(-np.pi / 2, np.pi / 2, size=self.n_dims)
        xc = self.learn_rate * self.T * np.tan(u)
        x_new = x + xc
        return x_new

    def cool_down(self):
        self.T = self.T_max / (1 + self.iter_cycle)


# SA_fast is the default
SA = SAFast

class SA_TSP(SimulatedAnnealingBase):
    def cool_down(self):
        self.T = self.T_max / (1 + np.log(1 + self.iter_cycle))

    def get_new_x(self, x):
        x_new = x.copy()
        new_x_strategy = np.random.randint(3)
        if new_x_strategy == 0:
            x_new = mutation.swap(x_new)
        elif new_x_strategy == 1:
            x_new = mutation.reverse(x_new)
        elif new_x_strategy == 2:
            x_new = mutation.transpose(x_new)

        return x_new

demo_sa.py模拟退火的函数极值搜索案例，使用了一个著名的震荡函数，只能搜索到局部最优解，因为这个函数的极小值群体过于庞大

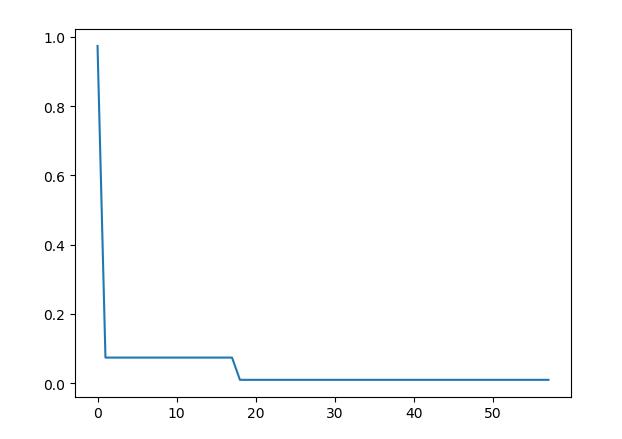
import numpy as np
# demo_func = lambda x: x[0] ** 2 + (x[1] - 0.05) ** 2 + x[2] ** 2
# 震荡函数，有无穷多个极小值点
demo_func = lambda x: 0.5+(np.square(np.sin(np.sqrt(x[0]**2+x[1]**2)))-0.5)/np.square(1+0.001*(x[0]**2+x[1]**2))

# %% Do SA
from sko.SA import SA

sa = SA(func=demo_func, x0=[1,1], T_max=1, T_min=1e-9, L=300, max_stay_counter=150)
best_x, best_y = sa.run()
print(\'best_x:\', best_x, \'best_y\', best_y)

# %% Plot the result
import matplotlib.pyplot as plt
import pandas as pd

plt.plot(pd.DataFrame(sa.best_y_history))
plt.show()

# %%
from sko.SA import SAFast

sa_fast = SAFast(func=demo_func, x0=[1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_fast.run()
print(\'Fast Simulated Annealing: best_x is \', sa_fast.best_x, \'best_y is \', sa_fast.best_y)

# %%
from sko.SA import SABoltzmann

sa_boltzmann = SABoltzmann(func=demo_func, x0=[1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_boltzmann.run()
print(\'Boltzmann Simulated Annealing: best_x is \', sa_boltzmann.best_x, \'best_y is \', sa_fast.best_y)

# %%
from sko.SA import SACauchy

sa_cauchy = SACauchy(func=demo_func, x0=[1, 1], T_max=1, T_min=1e-9, q=0.99, L=300, max_stay_counter=150)
sa_cauchy.run()
print(\'Cauchy Simulated Annealing: best_x is \', sa_cauchy.best_x, \'best_y is \', sa_cauchy.best_y)

得到的函数值下降曲线为

 

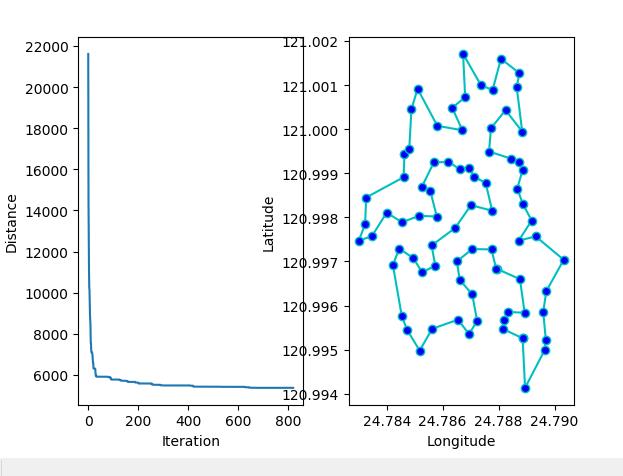
 TSP问题的优化以及动态迭代过程展示

import numpy as np
from scipy import spatial
import matplotlib.pyplot as plt
import sys

file_name = sys.argv[1] if len(sys.argv) > 1 else \'data/nctu.csv\'
points_coordinate = np.loadtxt(file_name, delimiter=\',\')
num_points = points_coordinate.shape[0]
distance_matrix = spatial.distance.cdist(points_coordinate, points_coordinate, metric=\'euclidean\')
distance_matrix = distance_matrix * 111000  # 1 degree of lat/lon ~ = 111000m


def cal_total_distance(routine):
    \'\'\'The objective function. input routine, return total distance.
    cal_total_distance(np.arange(num_points))
    \'\'\'
    num_points, = routine.shape
    return sum([distance_matrix[routine[i % num_points], routine[(i + 1) % num_points]] for i in range(num_points)])


# %%
from sko.SA import SA_TSP

sa_tsp = SA_TSP(func=cal_total_distance, x0=range(num_points), T_max=100, T_min=1, L=10 * num_points)

best_points, best_distance = sa_tsp.run()
print(best_points, best_distance, cal_total_distance(best_points))
# %% Plot the best routine
from matplotlib.ticker import FormatStrFormatter

fig, ax = plt.subplots(1, 2)

best_points_ = np.concatenate([best_points, [best_points[0]]])
best_points_coordinate = points_coordinate[best_points_, :]
ax[0].plot(sa_tsp.best_y_history)
ax[0].set_xlabel("Iteration")
ax[0].set_ylabel("Distance")
ax[1].plot(best_points_coordinate[:, 0], best_points_coordinate[:, 1],
           marker=\'o\', markerfacecolor=\'b\', color=\'c\', linestyle=\'-\')
ax[1].xaxis.set_major_formatter(FormatStrFormatter(\'%.3f\'))
ax[1].yaxis.set_major_formatter(FormatStrFormatter(\'%.3f\'))
ax[1].set_xlabel("Longitude")
ax[1].set_ylabel("Latitude")
plt.show()

# %% Plot the animation
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

best_x_history = sa_tsp.best_x_history

fig2, ax2 = plt.subplots(1, 1)
ax2.set_title(\'title\', loc=\'center\')
line = ax2.plot(points_coordinate[:, 0], points_coordinate[:, 1],
                marker=\'o\', markerfacecolor=\'b\', color=\'c\', linestyle=\'-\')
ax2.xaxis.set_major_formatter(FormatStrFormatter(\'%.3f\'))
ax2.yaxis.set_major_formatter(FormatStrFormatter(\'%.3f\'))
ax2.set_xlabel("Longitude")
ax2.set_ylabel("Latitude")
plt.ion()
p = plt.show()


def update_scatter(frame):
    ax2.set_title(\'iter = \' + str(frame))
    points = best_x_history[frame]
    points = np.concatenate([points, [points[0]]])
    point_coordinate = points_coordinate[points, :]
    plt.setp(line, \'xdata\', point_coordinate[:, 0], \'ydata\', point_coordinate[:, 1])
    return line


ani = FuncAnimation(fig2, update_scatter, blit=True, interval=25, frames=len(best_x_history))
plt.show()

# ani.save(\'sa_tsp.gif\', writer=\'pillow\')

data/nctu.csv 文件

24.783003,120.997474
24.785737,120.996905
24.784604,120.998911
24.785261,120.998698
24.785266,120.996754
24.784001,120.998107
24.783266,120.99845
24.785178,120.994979
24.784736,120.995445
24.785626,120.995474
24.784542,120.995755
24.788155,120.99547
24.788339,120.995857
24.78886,120.995259
24.788192,120.995671
24.786551,120.995681
24.787233,120.995651
24.786942,120.995354
24.788947,120.994135
24.789596,120.995856
24.78969,120.995223
24.789652,120.994996
24.788933,120.995836
24.789182,120.997927
24.786731,121.001706
24.787541,120.998777
24.786444,120.997757
24.788442,120.999333
24.787059,120.996254
24.788719,120.997473
24.787729,121.000022
24.786509,120.997
24.787374,121.000994
24.787748,120.997273
24.789707,120.99633
24.785103,121.000918
24.787056,120.997282
24.785563,120.998591
24.79033,120.997038
24.785684,120.999245
24.788844,120.999945
24.789328,120.997568
24.786955,120.999126
24.78872,120.999253
24.78777,120.998151
24.788856,120.999068
24.787943,120.996833
24.788764,120.996599
24.784636,120.999428
24.784805,120.99954
24.784957,120.997073
24.783229,120.997842
24.785159,120.998036
24.787014,120.998277
24.787786,121.000889
24.788249,121.000433
24.78445,120.997293
24.786209,120.999259
24.788648,121.000958
24.787658,120.999493
24.784886,121.000451
24.78455,120.997889
24.786806,121.000725
24.786624,120.999088
24.784222,120.996917
24.787919,120.996822
24.788746,121.001269
24.788667,120.998652
24.783467,120.997571
24.788086,121.001596
24.788868,120.998306
24.786342,121.000484
24.785605,120.997364
24.787122,120.998925
24.785791,120.998019
24.786612,120.996584
24.786708,120.999975
24.78581,121.000076

 

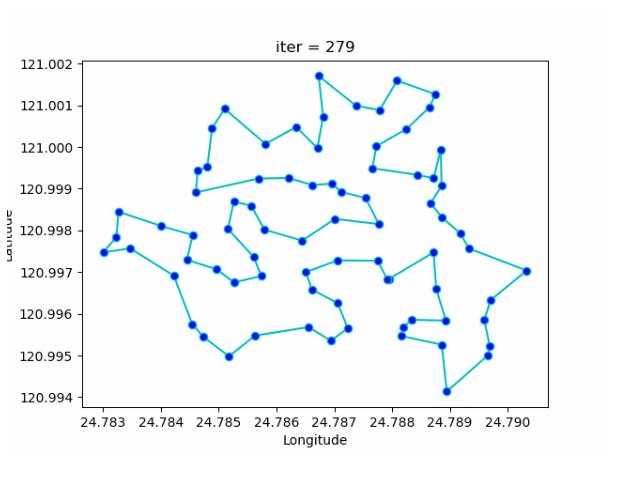
 gif迭代过程展示，gif太大无法展示，可以通过上面的Python源码运行后进行保存即可，根据每次迭代，动态更新的，可以看出TSP问题求解的过程