[Week 19]每日一题(C++,数学,并查集,动态规划)
Posted witheredsakura
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[Week 19]每日一题(C++,数学,并查集,动态规划)相关的知识,希望对你有一定的参考价值。
[Daimayuan] T1 倒数第n个字符串(C++,进制)
给定一个完全由小写英文字母组成的字符串等差递增序列,该序列中的每个字符串的长度固定为 \\(L\\),从 \\(L\\) 个 \\(a\\) 开始,以 \\(1\\) 为步长递增。例如当 \\(L\\) 为 \\(3\\) 时,序列为 \\(aaa,aab,aac,...,aaz,aba,abb,...,abz,...,zzz\\)。这个序列的倒数第 \\(2\\) 个字符串就是 \\(zzy\\)。对于任意给定的 \\(L\\),本题要求你给出对应序列倒数第 \\(N\\) 个字符串。
输入格式
输入在一行中给出两个正整数 \\(L\\) (\\(1≤L≤6\\))和 \\(N\\)( \\(N≤10^5\\)).
注意:数据范围有修改!!!
输出格式
在一行中输出对应序列倒数第 \\(N\\) 个字符串。题目保证这个字符串是存在的。
样例输入
6 789
样例输出
zzzyvr
解题思路
把字符串看作\\(26\\)进制:
0->a
1->b
2->c
...
25->z
然后把我们进制转换的辗转相除法拿出来:
int idx = len - 1;
while (num)
arr[idx--] = -(num % 26);
num /= 26;
最后用zzz...z减去我们求得的\\(26\\)进制串即可。
AC代码如下:
#include <iostream>
using namespace std;
const int max_len = 10;
const int max_num = 1e5;
int arr[max_len];
int main()
int len, num;
cin >> len >> num;
num--;
int idx = len - 1;
while (num)
arr[idx--] = -(num % 26);
num /= 26;
for (int i = 0; i < len; i++)
printf("%c", char(arr[i] + 122));
return 0;
[Daimayuan] T2 排队(C++,并查集)
请判断有没有一种方法可以将编号从 \\(1\\) 到 \\(N\\) 的 \\(N\\) 个人排成一排,并且满足给定的 \\(M\\) 个要求。
对于每个要求会给出两个整数 \\(A_i\\) 和 \\(B_i\\),表示编号 \\(A_i\\) 和 \\(B_i\\) 的人是相邻的。
保证每个要求都不同,比如已经给出了 \\(1,5\\),就不会再给出 \\(1,5\\) 或 \\(5,1\\)。
输入格式
第一行两个整数 \\(N\\) 和 \\(M\\),表示 \\(N\\) 个人和 \\(M\\) 个要求。
输出格式
如果有一种能把这些人拍成一排并满足所有条件的方法,就输出 Yes,否则,输出 No。
样例输入1
4 2
1 3
2 3
样例输出1
Yes
样例输入2
4 3
1 4
2 4
3 4
样例输出2
No
样例输入3
3 3
1 2
1 3
2 3
样例输出3
No
数据规模
对于全部数据保证 \\(2≤N≤10^5\\),\\(0≤M≤10^5\\),\\(1≤A_i<B_i≤N\\)。
解题思路
本题是一道逻辑推理题。
我们推理的基础就是:一个人最多与两个人相邻。
根据这个定理,我们可以得出以下规律:
(1)在\\(M\\)个要求中,一个人最多出现两次;
(2)因为是队列不是环,队首和队尾不可能相邻。
条件\\(1\\)很容易就能用数组维护;
条件\\(2\\)采用并查集维护(常用于强连通分量),思路是任意两个元素只会被合并一次,所以当尝试合并在同一个集合中的元素时,判断不合理。最后,AC代码如下:
#include <iostream>
#include <vector>
using namespace std;
const int max_len = 1e5;
int fa[max_len + 1], sum[max_len + 1];
int find(int x)
return x == fa[x] ? x : (fa[x] = find(fa[x]));
bool is_insame(int x, int y)
x = find(x); y = find(y);
return x == y;
void merge(int x, int y)
x = find(x); y = find(y);
fa[x] = y;
int main()
int n, m, x, y, flag = 0;
cin >> n >> m;
for (int i = 1; i <= n; i++) fa[i] = i;//并查集初始化
for (int i = 0; i < m; i++)
cin >> x >> y;
if (!flag)
if (sum[x] < 2 && sum[y] < 2) //一个人最多与两个人相邻
if (is_insame(x, y)) //成环
flag = 1;
else
merge(x, y);
sum[x]++; sum[y]++;
else flag = 1;
if (flag) cout << "No" << endl;
else cout << "Yes" << endl;
return 0;
[Daimayuan] T3 素数之欢(C++,BFS)
现给定两个 四位素数 \\(a,b\\)。 你可以执行多次下面的操作:
修改数字 \\(a\\) 的某一位, 使其成为另一个 四位素数。
例如,\\(1033→1733\\),其中 \\(1033\\) 与 \\(1733\\) 均为素数。
问至少多少次变换后能从 \\(a\\) 得到 \\(b\\) ? 或回答不可能。
数据规模
- 多组数据 \\(1≤T≤100\\)
输入格式
第一行一个数字 \\(T\\),表示接下来将会有 \\(T\\) 组数据。
接下来包含 \\(T\\) 行,每行包含用空格分开的两个 四位素数 \\(a,b\\)。
输出格式
输出 \\(T\\) 行,如果可以,输出最小变换次数。反之输出 \\(−1\\)。
样例输入
2
1033 1033
1033 8779
样例输出
0
5
说明
\\(1033→1733→3733→3739→3779→8779\\)
tips: you only operate \\(8\\) times if possible.
解题思路
找出规律困难,数据规模不大,于是考虑暴力搜索。
每次对四位数都尝试一次变换,每位数有九种变换的可能,那么每轮的操作次数就是\\(9^4=6561\\)
对于每组测试数据,提示说明我们最多会进行\\(8\\)次尝试,所以每组测试数据的最多操作次数为\\(6561*8=52488\\)
最多有\\(100\\)组测试数据,所以最多累加操作次数为\\(5248800≈5*10^6\\)
时间复杂度可以接受,爆搜开始。
采用广度优先搜索还是深度优先搜索?。
深度优先搜索与广度优先搜索不同在于:
深度优先搜索会尝试每一种可能的解决方法;
广度优先搜索保证搜索到的解决方法中每一步都是最少步骤。
显然广度优先搜索更适合本题的爆搜。
然后是代码实现:
(1)常规的\\(BFS\\)算法:
bool vis[max_n]; //访问标记物
queue<pair<int, int>>q; //前者为数字,后者为操作次数
//队列初始化
q.push( num1,0 );
vis[num1] = true;
while (!q.empty())
//取出队首
q.front();
q.pop();
//BFS主体
for (/* 对每一位进行尝试 */)
for (/* 变换9种数字 */)
int temp;
if (temp == num2) //结束条件
break;
else (!vis[temp] && prime.count(temp)) //继续搜索
q.push( temp, step + 1 );
vis[temp] = true;
保证每一步都是最小步骤数。
(2)素数判断:
注意到这里有一个prime集合用于素数判断,这里提供两种方法制作素数集合:
常规方法:
void PrimeList(int n)
for (int i = 2; i <= n; i++)
bool flag = true;
for (int j = 2; j * j <= i; j++)
if (i % j == 0)
flag = false;
break;
if (flag) prime.insert(i);
欧拉筛(欧拉筛传送门):
void PrimeList(int* Prime, bool* isPrime, int n)
/* 欧拉筛 */
int i = 0, j = 0, count = 0;
memset(isPrime, true, sizeof(bool) * (n + 1));
isPrime[0] = isPrime[1] = false;
for (i = 2; i <= n; i++)
if (isPrime[i])
Prime[count++] = i;
prime.insert(i);
for (j = 0; j < count && Prime[j] * i <= n; j++)
isPrime[i * Prime[j]] = false;
//欧拉筛核心,每一个合数都能拆成最小因数与最大因数的乘积
if (i % Prime[j] == 0) break;
最后,AC代码如下
#include <iostream>
#include <string.h>
#include <queue>
#include <set>
using namespace std;
const int max_t = 100;
const int max_epoch = 8;
const int max_n = 10000;
bool isPrime[max_n], vis[max_n];
int Prime[max_n];
set<int>prime;
void PrimeList(int* Prime, bool* isPrime, int n)
/* 欧拉筛 */
int i = 0, j = 0, count = 0;
memset(isPrime, true, sizeof(bool) * (n + 1));
isPrime[0] = isPrime[1] = false;
for (i = 2; i <= n; i++)
if (isPrime[i])
Prime[count++] = i;
prime.insert(i);
for (j = 0; j < count && Prime[j] * i <= n; j++)
isPrime[i * Prime[j]] = false;
//欧拉筛核心,每一个合数都能拆成最小因数与最大因数的乘积
if (i % Prime[j] == 0) break;
//void PrimeList(int n)
// for (int i = 2; i <= n; i++)
// bool flag = true;
// for (int j = 2; j * j <= i; j++)
// if (i % j == 0)
// flag = false;
// break;
//
//
// if (flag) prime.insert(i);
//
//
int main()
PrimeList(Prime, isPrime, max_n);
//PrimeList(max_n);
int t, num1, num2;
cin >> t;
while (t--)
cin >> num1 >> num2;
if (num1 == num2) //特判
cout << 0 << endl;
continue;
queue<pair<int, int>>q; //初始化队列
memset(vis, false, sizeof(bool) * (max_n));
vis[num1] = true;
q.push( num1,0 );
bool flag = true; //初始化标记物
int ans = -1;
while (flag && !q.empty())
int num3 = q.front().first, step = q.front().second;
q.pop();
for (int i = 1; flag && i <= 1000; i *= 10) //对每一位进行尝试
int num4 = num3 / i / 10 * 10 * i + num3 % i;
for (int j = 0; flag && j < 10; j++) //变换9种数字
int num5 = num4 + j * i;
if (num5 == num2) //找到数字
flag = false;
ans = step + 1;
break;
if (!vis[num5] && prime.count(num5)) //未找到,但是为质数
q.push( num5,step + 1 );
vis[num5] = true;
cout << ans << endl;
return 0;
[Daimayuan] T4 国家铁路(C++,数学,动态规划)
题目描述
\\(dls\\)的算竞王国可以被表示为一个有 \\(H\\)行和 \\(W\\)列的网格,我们让 \\((i,j)\\)表示从北边第\\(i\\)行和从西边第\\(j\\)列的网格。最近此王国的公民希望国王能够修建一条铁路。
铁路的修建分为两个阶段:
- 从所有网格中挑选\\(2\\)个不同的网格,在这两个网格上分别修建一个火车站。在一个网络上修建一个火车站的代价是\\(A_i,j\\)。
- 在这两个网格间修建一条铁轨,假设我们选择的网格是 \\((x_1,y_1)\\)和\\((x_2,y_2)\\),其代价是 \\(C×(|x_1−x_2|+|y_1−y_2|)\\)。
\\(dls\\)的愿望是希望用最少的花费去修建一条铁路造福公民们。现在请你求出这个最小花费。
题目输入
第一行输入三个整数分别代表\\(H,W,C(2≤H,W≤1000,1≤C≤10^9)\\)。
接下来\\(H\\)行,每行\\(W\\)个整数,代表\\(A_i,j(1≤A_i,j≤10^9)\\)。
题目输出
输出一个整数代表最小花费。
样例输入1
3 4 2
1 7 7 9
9 6 3 7
7 8 6 4
样例输出1
10
样例输入2
3 3 1000000000
1000000 1000000 1
1000000 1000000 1000000
1 1000000 1000000
样例输出2
1001000001
解题思路
这道题有亿点点难QAQ。
直接枚举的时间复杂度为\\(o(n^4)\\),直接\\(T\\)飞,所以我们需要想办法优化。
题中给出,修建一条铁轨的总花费为\\(A_x_1,y_1+A_x_2,y_2+C*(|x_1-x_2|+|y_1-y_2|)\\)。
显然,交换一下\\((x_1,y_1)\\)和\\((x_2,y_2)\\)的坐标对花费没有任何影响。
所以,为了方便计算,我们规定情况\\(1\\)为\\(x_1\\ge x_2,y_1\\ge y_2\\),情况\\(2\\)为\\(x_1\\ge x_2,y_1\\le y_2\\)。
直观的来说,以上两种情况分别为矩阵的主对角线方向和副对角线方向。
只需要讨论一种情况的算法,另外一种情况则不证自明:
对于情况\\(1\\),总花费可以写为:
在公式的形式简化之后,再去考虑寻找最小值的问题:
我们发现对于给定的\\((x_1,y_1)\\),我们需要枚举所有符合条件的\\((x_2,y_2)\\)(条件为\\(x_1\\ge x_2,y_1\\ge y_2\\),在一个小矩阵中),并找出最小值。
但与之前不同,我们现在可以对\\((x_2,y_2)\\)进行动态规划,然后就可以在\\(O(1)\\)时间内获取对于给定\\((x_1,y_1)\\)的最小值。
规划公式为dp[i][j] = min dp[i][j-1], dp[i-1][j], station[i][j] - C * (i + j)。
for (int i = 1; i <= h; i++)
for (int j = 1; j <= w; j++)
dp[i][j] = min(dp[i][j - 1], min(dp[i - 1][j], station[i][j] - C * (i + j)));
那么计算主对角线情况下的最小值,只需要枚举另外一个点:
for (int i = 1; i <= h; i++)
for (int j = 1; j <= w; j++)
ans = min(ans, min(dp[i - 1][j] + dp[i][j - 1]) + station[i][j] + C * (i + j));
最后简单给出计算副对角线情况下最小值的代码以及AC代码:
副对角线算法:
for (int i = 1; i <= h; i++)
for (int j = w; j >= 1; j--)
dp[i][j] = min(dp[i][j + 1], min(dp[i - 1][j], station[i][j] + C * (j - i)));
for (int i = 1; i <= h; i++)
for (int j = 1; j <= w; j++)
ans = min(ans, min(dp[i - 1][j], dp[i][j + 1]) + station[i][j] + C * (i - j));
AC代码:
#include <iostream>
#include <string.h>
using namespace std;
const long long max_h = 1000;
const long long max_w = 1000;
const long long NaN = 0x3F3F3F3F3F3F3F3F;
const long long max_c = 1e9;
long long station[max_h + 2][max_w + 2], dp1[max_h + 2][max_w + 2], dp2[max_h + 2][max_w + 2]; //多开一圈,防止越界
long long h, w, C;
int main()
cin >> h >> w >> C;
for (int i = 1; i <= h; i++)
for (int j = 1; j <= w; j++)
cin >> station[i][j];
//DP1(主对角线)
memset(dp1, 0x3F, sizeof(long long) * (max_h + 2) * (max_w + 2));
for (int i = 1; i <= h; i++)
for (int j = 1; j <= w; j++)
dp1[i][j] = min(dp1[i - 1][j], min(dp1[i][j - 1], station[i][j] - C * (i + j)));
//DP2(副对角线)
memset(dp2, 0x3F, sizeof(long long) * (max_h + 2) * (max_w + 2));
for (int i = 1; i <= h; i++)
for (int j = w; j >= 1; j--)
dp2[i][j] = min(dp2[i][j + 1], min(dp2[i - 1][j], station[i][j] + C * (j - i)));
long long ans = NaN;
//ans1(主对角线)
for (int i = 1; i <= h; i++)
for (int j = 1; j <= w; j++)
ans = min(ans, min(dp1[i - 1][j], dp1[i][j - 1]) + station[i][j] + C * (i + j));
//ans2(副对角线)
for (int i = 1; i <= h; i++)
for (int j = 1; j <= w; j++)
ans = min(ans, min(dp2[i - 1][j], dp2[i][j + 1]) + station[i][j] + C * (i - j));
cout << ans << endl;
return 0;
[Daimayuan] T5 吃糖果(C++,贪心)
桌子上从左到右放着 \\(n\\) 个糖果。糖果从左到右编号,第 \\(i\\) 块糖果的重量为 \\(w_i\\)。小明和小红要吃糖果。
小明从左边开始吃任意数量的糖果。(连续吃,不能跳过糖果)
小红从右边开始吃任意数量的糖果。(连续吃,不能跳过糖果)
当然,如果小明吃了某个糖果,小红就不能吃它(反之亦然)。
他们的目标是吃同样重量的糖果,请问此时他们总共最多能吃多少个糖果?
输入格式
第一行包含一个整数 \\(n\\),表示桌上糖果的数量。
第二行包含 \\(n\\) 个整数 \\(w_1,w_2,…,w_n\\),表示糖果从左到右的重量。
输出格式
一个整数,表示小明和小红在满足条件的情况下总共可以吃的糖果的最大数量。
数据范围
\\(1≤n≤2*10^5,1≤w_i≤10^4\\)
输入样例
9
7 3 20 5 15 1 11 8 10
输出样例
7
解题思路
采用贪心算法(不断尝试吃更多的糖)解决此题:
初始化规定糖的重量相等,然后循环分支:
(1)糖的重量相等,记录当前总共吃了多少颗糖,双方再吃一颗糖;
(2)糖的重量不相等,吃的少的一方再吃一颗糖。
结束条件:双方吃糖发生冲突(题目规定:“如果小明吃了某个糖果,小红就不能吃它(反之亦然)”)。
AC代码如下:
#include <iostream>
using namespace std;
const int max_n = 2e5;
const int max_w = 1e4;
int candies[max_n];
int main()
int n;
cin >> n;
for (int i = 0; i < n; i++) cin >> candies[i];
int l = 0, r = n - 1, l_sum = 0, r_sum = 0, ans = 0;
while (l < r)
if (l_sum == r_sum)
ans = l - 0 + n - 1 - r;
l_sum += candies[l++];
r_sum += candies[r--];
else if (l_sum < r_sum) l_sum += candies[l++];
else r_sum += candies[r--];
cout << ans << endl;
return 0;
贪心证明:
初始化,规定双方吃糖量相同,吃糖数目为\\(0\\)。
为了确定是否存在比\\(0\\)大的解,我们必须要让其中一方吃一颗糖。
那么这就会导致双方吃糖量不等,要让其相等,我们必须让另一方吃一颗糖。
只要不平衡,我们就需要让吃的少的那一方继续吃。
当平衡的时候,设吃糖数目为\\(ans\\)。
为了确定是否存在比\\(ans\\)大的解,我们必须要让其中一方吃一颗糖...(依次类推,直到发生冲突)
[Daimayuan] T6 切割(C++,贪心,哈夫曼树)
题目描述
有一个长度为 \\(\\sum a_i\\) 的木板,需要切割成 \\(n\\) 段,每段木板的长度分别为 \\(a_1,a_2,…,a_n\\)。
每次切割,会产生大小为被切割木板长度的开销。
请你求出将此木板切割成如上 \\(n\\) 段的最小开销。
输入格式
第 \\(1\\) 行一个正整数表示 \\(n\\)。
第 \\(2\\) 行包含 \\(n\\) 个正整数,即 \\(a_1,a_2,…,a_n\\)。
输出格式
输出一个正整数,表示最小开销。
样例输入
5
5 3 4 4 4
样例输出
47
数据范围
对于全部测试数据,满足 \\(1≤n,a_i≤10^5\\)。
附加说明
原题:[NOIP2004 提高组] 合并果子 / [USACO06NOV] Fence Repair G
需要 O(n) 解法的 数据加强版(\\(1≤n≤10^7\\))
解题思路
首先我们采用逆向思维,改变题意为:
把\\(n\\)块长度分别为 \\(a_1,a_2,…,a_n\\)的木板合并成一块,每次合并只能操作两块,会产生合并后木板长度的开销。
可以很容易发现这和题意描述是一样的。
然后引入核心思路:哈夫曼树。
哈夫曼树常用于数据压缩(本质上是编码方式),基本思想就是:
统计文本中的所有符号的词频,每次选择词频最低的两个进行操作,将它们连到一个新的父节点上,然后将父节点赋值为二者词频之和,直到生成一棵树。
这种方式能够保证词频越小的节点深度越深(编码长度越长),词频越高的节点深度越浅(编码长度越短),也就完成了数据压缩。
那么这和本题有什么关系?
我们可以认为哈夫曼树中的叶子节点就是\\(n\\)块木板,节点深度就是木板被操作的次数。
(注:我们可以把合并后的木板仍然看成是多块木板,只不过这几块木板可以一起操作。)
所以,深度越深也就代表着这块木板被操作的次数越多,深度越浅也就代表着这块木板被操作的次数越少。
故哈夫曼树算法能够保证最小开销。
代码实现:
采用优先队列维护木板,每次取出两块进行合并,然后将合并后的木板插入队列。
AC代码如下:
(前排提示:/* 十年OI一场空,不开long long见祖宗 */)
#include <iostream>
#include <queue>
using namespace std;
const int max_n = 1e5;
const int max_a = 1e5;
priority_queue<long long, vector<long long>, greater<long long>>pq;
int main()
long long n, temp;
cin >> n;
for (int i = 0; i < n; i++)
cin >> temp;
pq.push(temp);
long long ans = 0;
while (pq.size() > 1)
long long b1 = pq.top(); pq.pop();
long long b2 = pq.top(); pq.pop();
pq.push(b1 + b2);
ans += (long long)(b1) + (long long)(b2);
cout << ans << endl;
return 0;
后排推一下我写的合并果子\\(qwq\\)
然后是数据加强版合并果子:
贪心算法是不能优化的了,可以优化的地方在于优先队列。
因为我们每次将合并后的果堆插入队列中,队列都会运行排序算法找到应该插入的位置。
优化的前提是这样的:
每次合并后的果堆一定不会比上一次合并得到的果堆小。
那么我们就不需要将其插入优先队列,只需要另外维护一个队列用来存储合并后的果堆,然后每次取出两个队列中队首比较小的一个即可。
直观的思路是这样的:
首先采用比快速排序更快的排序算法桶排序,将果堆维护在一个有序队列中;
然后再维护一个队列用于存储合并后的果堆;
最后运行的贪心算法与之前一致。
AC代码如下:
#include <iostream>
#include <queue>
#include <cstdio>
#include <cstdlib>
using namespace std;
const int max_a = 1e5;
queue<long long>q1, q2;
int buckets[max_a + 1];
int main()
int n, temp;
scanf("%d", &n);
for (int i = 0; i < n; i++)
scanf("%d", &temp);
buckets[temp]++;
for (int i = 1; i <= max_a; i++)
while (buckets[i]--)
q1.push((long long)(i));
long long t1, t2, ans = 0;
for (int i = 1; i < n; i++)
if (q2.empty() || !q1.empty() && q1.front() < q2.front())
t1 = q1.front();
q1.pop();
else
t1 = q2.front();
q2.pop();
if (q2.empty() || !q1.empty() && q1.front() < q2.front())
t2 = q1.front();
q1.pop();
else
t2 = q2.front();
q2.pop();
q2.push(t1 + t2);
ans += t1 + t2;
cout << ans << endl;
return 0;
其实这段代码还会\\(T\\),怎么优化?当然是用无敌的快读了:
void read(int& x)
x = 0;
char c = getchar();
while (\'0\' <= c && c <= \'9\')
x = x * 10 + c - \'0\';
c = getchar();
[Daimayuan] T7 异或和(C++,异或,数学)
给定一个长度为 \\(n\\) 的数组 \\(a_1,a_2,...,a_n\\)。 请你求出下面式子的模\\(1e9+7\\)的值。
\\(\\sum_i=1^n-1\\sum_j=i+1^n(a_i\\ XOR\\ a_j)\\)
输入格式
第一行一个数字 \\(n\\)。
接下来一行 \\(n\\) 个整数 \\(a_1,a_2,…,a_n\\)。
输出格式
一行一个整数表示答案。
样例输入
3
1 2 3
样例输出
6
数据规模
所有数据保证 \\(2≤n≤300000,0≤a_i<2^60\\)。
解题思路
依照题意,我们只能直接跑二重循环(因为\\(a_i\\)和\\(a_j\\)的组合不会重复,也就是说没有子结构的概念),这肯定会\\(TLE\\)。
那么我们考虑异或操作的性质:
异或操作是位操作,无视整个位串的意义,只能看到单个位。——条件(1)
然后重新审视\\(\\sum_i=1^n-1\\sum_j=i+1^n(a_i\\ XOR\\ a_j)\\)。
这个式子就是对任意两个元素进行异或操作然后做和,也就是说尝试了所有的组合(\\(C_n^2\\))。——条件(2)
再来看一下异或操作的性质:同则为假,不同为真。——条件(3)
如何利用三个条件优化算法?这里通过一个简单的例子来理解:
有位串\\(1000 0111\\),我们对任意两个位进行异或操作,然后做和。很容易发现,其和为\\(4*4=16\\)。就是\\(1\\)的数量乘上\\(0\\)的数量。
然后我们回去看一眼题中的例子:
1 2 3
1 1 0 1 -> 2 * 1 = 2
2 0 1 1 -> 2 * 2 = 4
4 0 0 0 -> 0 * 4 = 0
比起之前那个简单的例子,也就是多了个权重,仅此而已。
接下来简单说一下代码如何实现:
我们维护每一个位上\\(1\\)(也可以是\\(0\\))出现的次数;
然后遍历每一个位,累计:\\(0\\)的数量\\(*1\\)的数量\\(*\\)权重。
AC代码如下:
#include <iostream>
using namespace std;
const int max_len = 60;
const long long max_a = (1LL << 60LL) - 1LL;
const int max_n = 300000;
const long long mod_num = 1e9 + 7;
long long sum[max_len];
inline void read()
long long x, idx = 0;
cin >> x;
while (x)
sum[idx++] += x & 1;
x >>= 1;
int main()
int n;
cin >> n;
for (int i = 0; i < n; i++) read();
long long ans = 0;
for (int i = 0; i < max_len; i++)
long long power = (1LL << (long long)(i)) % mod_num;
long long comb = sum[i] * (n - sum[i]) % mod_num;
ans = (ans + (power * comb) % mod_num) % mod_num;
cout << ans << endl;
return 0;
[Daimayuan] T8 分数拆分(C++,数学)
输入正整数 \\(k\\),找到所有的正整数 \\(y≤x\\), 使得 \\(\\frac1k=\\frac1x+\\frac1y\\)。
输入格式
输入一个正整数 \\(k(1≤k≤10^7)\\)。
输出格式
输出一个数,表示满足条件的\\(x,y\\)的个数。
样例输入
12
样例输出
8
解题思路
题目要求很好理解:找出的\\(x,y\\)使得\\(k=\\fracxy(x+y)\\)。
那么如何找出这样的\\(x,y\\)?或者说,如何找到\\(x,y\\)中的一个?
我们进一步把公式变换为\\(y=\\frackxx-k\\)(其中\\(k < x \\le y\\))。
但是仍然不好求解。
那么进一步研究公式的形式,有\\(x=k+b(b>0)\\),那么有:
\\(y=\\frack^2+bkb\\)
于是有\\(k^2\\ mod\\ b =0\\)和\\(bk\\ mod\\ b=0\\)。
根据前者,我们可以知道\\(b\\)是\\(k^2\\)的因子,第二个条件是显然成立的。
再考虑\\(x\\le y\\)这个条件,根据题意有\\(x\\le 2k\\),则有\\(b\\le k\\)。
那么求解就变得容易了,我们枚举因子即可,时间复杂度为\\(o(k)\\)。
最后,AC代码如下:
#include <iostream>
using namespace std;
long long max_k = 1e7;
int main()
long long k, x, y, ans = 0;
cin >> k;
long long temp = k * k;
for (long long i = 1; i <= k; i++)
if (temp % i == 0)
ans++;
cout << ans << endl;
return 0;
[Daimayuan] T9 简单子段和(C++,前缀和)
给出一个长为 \\(N\\) 的整数数组 \\(A\\) 和一个整数 \\(K\\)。
请问有数组 \\(A\\) 中有多少个子数组,其元素之和为 \\(K\\)?
输入格式
第一行两个整数 \\(N\\) 和 \\(K\\),表示数组 \\(A\\) 的大小,和给出的整数 \\(K\\)。
第二行 \\(N\\) 个整数,表示数组 \\(A\\) 中的每个元素 \\(A_1,...,A_n\\)。
输出格式
输出一个整数,表示答案。
样例输入1
6 5
8 -3 5 7 0 -4
样例输出1
3
有三个子数组 (\\(A_1,A_2\\)),(\\(A_3\\)),(\\(A_2,...,A_6\\))满足条件。
样例输入2
2 -1000000000000000
1000000000 -1000000000
样例输出2
0
数据规模
对于全部数据保证 \\(1≤N≤2×10^5\\),\\(|A_i|≤10^9\\),\\(|k|≤10^15\\)。
解题思路
直接枚举的时间复杂度是\\(O(N^2)\\),必然\\(TLE\\),所以考虑优化。
对于连续区间和问题,我们常常会使用前缀和。
前缀和很好理解,也很好实现,但是怎么应用到这道题中?
观察这个式子:\\(k=pre-(pre-k)\\)。(这不是废话嘛)
\\(pre\\)和\\(pre-k\\)代表着两个前缀和。
那么现在我们只需要遍历每一个\\(pre\\),统计相应的\\(pre-k\\)数目即可。
这里采用在线做法实现:
(1)动态更新当前的前缀和;
(2)计算\\(pre-k\\)的数量;
(3)前缀和\\(pre\\)的数量++。
AC代码如下:
#include <iostream>
#include <cstdlib>
#include <cstdio>
#include <map>
using namespace std;
const int max_n = 2e5;
const int max_a = 1e9;
const long long max_k = (long long)(1e10) * (long long)(1e5);
map<long long, int>m;
int main()
long long n, k, temp, sum = 0, ans = 0;
m.insert( 0LL,1 );
cin >> n >> k;
//scanf("%lld%lld", &n, &k);
for (int i = 1; i <= n; i++)
cin >> temp;
//scanf("%lld", &temp);
sum += temp;
if (m.find(sum - k) != m.end())
ans += m[sum - k];
m[sum]++;
cout << ans << endl;
return 0;
[Daimayuan] T10 Good Permutations(C++,数学)
对于每一个长度为 \\(n\\) 的排列 \\(a\\),我们都可以按照下面的两种方式将它建成一个图:
1.对于每一个 \\(1≤i≤n\\),找到一个最大的 \\(j\\) 满足 \\(1≤j<i,a_j>a_i\\),将 \\(i\\) 和 \\(j\\) 之间建一条无向边
2.对于每一个 \\(1≤i≤n\\),找到一个最小的 \\(j\\) 满足 \\(i<j≤n,a_j>a_i\\),将 \\(i\\) 和 \\(j\\) 之间建一条无向边
注意:建立的边是在对应的下标 \\(i,j\\) 之间建的边
请问有多少种长度为 \\(n\\) 的排列 \\(a\\) 满足,建出来的图含环
排列的数量可能会非常大,请输出它模上 \\(10^9+7\\) 后的值
输入描述
第 \\(1\\) 行给出 \\(1\\) 个数 \\(T(1≤T≤10^5)\\),表示有 \\(T\\) 组测试样例
第 \\(2\\) 到 \\(T+1\\) 行每行给出一个数 \\(n(3≤n≤10^6)\\),表示排列的长度
输出描述
输出符合条件的排列的数量模上 \\(10^9+7\\) 后的值
样例输入
1
4
样例输出
16
解题思路
题意直观理解:\\(i\\)与\\(j\\)建边需要两个条件
(1)\\(a_i<a_j\\);
(2)要求索引距离最近。
设函数\\(f(x)=a_x\\),观察规律可以得到:只要函数存在极小值,那么就可以成环。
存在极小值的情况很多,正难则反,我们去求不可以成环的情况,也就是不存在极小值。
直观来看,不存在极小值的\\(f(x)\\)大致是这样的:
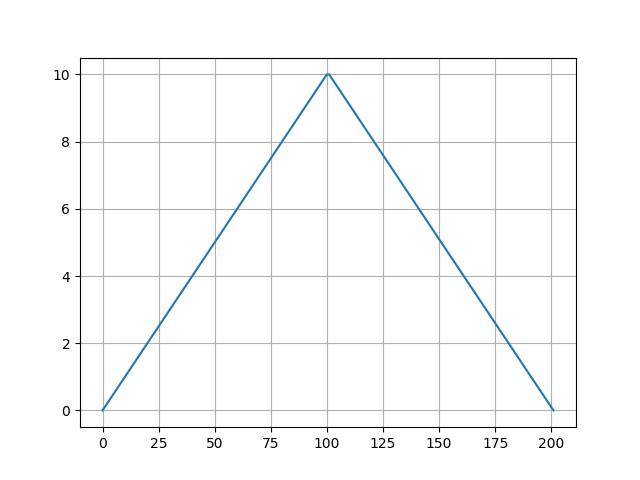
最大值点是固定的,我们只需要统计有多少种不同左右集合的组合:
\\(C^0_n-1+C^1_n-1+...+C^n-1_n-1=2^n-1\\)
所以计算公式为\\(ans=n!-2^n-1\\)。
最后,AC代码如下
#include <iostream>
using namespace std;
const long long mod_num = 1e9 + 7;
const long long max_n = 1e6;
long long factorial[max_n + 1], expo[max_n + 1];
void init()
//阶乘
factorial[0] = 1;
for (int i = 1; i <= max_n; i++)
factorial[i] = (factorial[i - 1] * (long long)(i)) % mod_num;
//2的i次幂
expo[0] = 1;
for (int i = 1; i <= max_n; i++)
expo[i] = (expo[i - 1] << 1LL) % mod_num;
long long solve(long long n)
long long ret = (factorial[n] - expo[n - 1]) % mod_num;
if (ret < 0) ret += mod_num;
return ret;
int main()
init();
long long T;
cin >> T;
while (T--)
long long n;
cin >> n;
cout << solve(n) << endl;
return 0;
hgame week2 week3
RE
1,babypy
对字节码硬怼,就可分析出大致逻辑是倒序后异或
c=[0x7d,0x03,0x7d,0x04,0x57,0x17,0x72,0x2d,0x62,0x11,0x4e,0x6a,0x5b,0x04,0x4f,0x2c,0x18,0x4c,0x3f,0x44,0x21,0x4c,0x2d,0x4a,0x22]
c.reverse()
flag=[]
for i in range(len(c)):
if i!=len(c)-1:
print(chr(c[i]^c[i+1]),end=‘‘)
else:
print(chr(c[i]))
得到flag
2,unpack
题如其名,手脱upx壳,虽然简单,但linux上还是第一次脱
用ida调试,f8不跑飞就不用f7,一直到

f7进去,再一直f8

到了一个跳转,f8
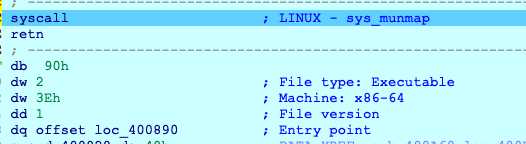
可以看到入口点0x400890,继续f8

来到了入口,dump出来
#include <idc.idc>
#define PT_LOAD 1
#define PT_DYNAMIC 2
static main(void)
{
auto ImageBase,StartImg,EndImg;
auto e_phoff;
auto e_phnum,p_offset;
auto i,dumpfile;
ImageBase=0x400000;
StartImg=0x400000;
EndImg=0x0;
if (Dword(ImageBase)==0x7f454c46 || Dword(ImageBase)==0x464c457f )
{
if(dumpfile=fopen("G:dumpfile","wb"))
{
e_phoff=ImageBase+Qword(ImageBase+0x20);
Message("e_phoff = 0x%x
", e_phoff);
e_phnum=Word(ImageBase+0x38);
Message("e_phnum = 0x%x
", e_phnum);
for(i=0;i<e_phnum;i++)
{
if (Dword(e_phoff)==PT_LOAD || Dword(e_phoff)==PT_DYNAMIC)
{
p_offset=Qword(e_phoff+0x8);
StartImg=Qword(e_phoff+0x10);
EndImg=StartImg+Qword(e_phoff+0x28);
Message("start = 0x%x, end = 0x%x, offset = 0x%x
", StartImg, EndImg, p_offset);
dump(dumpfile,StartImg,EndImg,p_offset);
Message("dump segment %d ok.
",i);
}
e_phoff=e_phoff+0x38;
}
fseek(dumpfile,0x3c,0);
fputc(0x00,dumpfile);
fputc(0x00,dumpfile);
fputc(0x00,dumpfile);
fputc(0x00,dumpfile);
fseek(dumpfile,0x28,0);
fputc(0x00,dumpfile);
fputc(0x00,dumpfile);
fputc(0x00,dumpfile);
fputc(0x00,dumpfile);
fputc(0x00,dumpfile);
fputc(0x00,dumpfile);
fputc(0x00,dumpfile);
fputc(0x00,dumpfile);
fclose(dumpfile);
}else Message("dump err.");
}
}
static dump(dumpfile,startimg,endimg,offset)
{
auto i;
auto size;
size=endimg-startimg;
fseek(dumpfile,offset,0);
for ( i=0; i < size; i=i+1 )
{
fputc(Byte(startimg+i),dumpfile);
}
}
再看dump出来的文件,用ida打开,
逻辑就十分简单了,脚本就不放了。
1,crackme
c#写的,关键代码
private void button1_Click(object sender, EventArgs e)
{
if (this.status == 1)
{
MessageBox.Show("你已经激活成功啦,快去提交flag吧~~~");
return;
}
string text = this.textBox1.Text;
if (text.Length != 46 || text.IndexOf("hgame{") != 0 || text.IndexOf("}") != 45)
{
MessageBox.Show("Illegal format");
return;
}
string base64iv = text.Substring(6, 24);
string str = text.Substring(30, 15);
try
{
Aes aes = new Aes("SGc0bTNfMm8yMF9XZWVLMg==", base64iv);
Aes aes2 = new Aes("SGc0bTNfMm8yMF9XZWVLMg==", "MFB1T2g5SWxYMDU0SWN0cw==");
string text2 = aes.DecryptFromBase64String("mjdRqH4d1O8nbUYJk+wVu3AeE7ZtE9rtT/8BA8J897I=");
if (text2.Equals("Same_ciphertext_"))
{
byte[] array = new byte[16];
Array.Copy(aes2.EncryptToByte(text2 + str), 16, array, 0, 16);
if (Convert.ToBase64String(array).Equals("dJntSWSPWbWocAq4yjBP5Q=="))
{
MessageBox.Show("注册成功!");
this.Text = "已激活,欢迎使用!";
this.status = 1;
}
else
{
MessageBox.Show("注册失败!
hint: " + aes2.DecryptFromBase64String("mjdRqH4d1O8nbUYJk+wVu3AeE7ZtE9rtT/8BA8J897I="));
}
}
else
{
MessageBox.Show("注册失败!
hint: " + aes2.DecryptFromBase64String("mjdRqH4d1O8nbUYJk+wVu3AeE7ZtE9rtT/8BA8J897I="));
}
}
catch
{
MessageBox.Show("注册失败!");
}
}
可见又是将输入分为两半,第一部分作为初始向量,使加密后的mjdRqH4d1O8nbUYJk+wVu3AeE7ZtE9rtT/8BA8J897I=变为Same_ciphertext_
第二部分将Same_ciphertext_和第二部分相加后加密为byte后将后十六位转为base64等于dJntSWSPWbWocAq4yjBP5Q==
就第一部分,已经得到了明文,密文,和密钥,根据aes加密的方式,只要将明文作为向量对密文进行解密就可得到真实的初始向量,
第二部分,因为只给了后半部分base64,将其转为十六进制,为了知道前面的部分,我以Same_ciphertext_123456789012345的格式进行加密,从而得到了其前半部分的十六进制,拼在一起后转为base64,再进行aes解密,得到第二部分
拼起来得到flag
hgame{L1R5WFl6UG5ZOyQpXHdlXw==DiFfer3Nt_w0r1d}
WEEK3
Misc
1,三重隐写
给了三个音频,其中一个播放时

扫码得到
AES key: 1ZmmeaLL^Typbcg3
第二个文件名有LSB可知是LSB隐写,用slienteye得到
Stegano key: uFSARLVNwVIewCY5
那么可猜到第三个音频是mp3隐写,用mp3stego得到
Zip Password: VvLvmGjpJ75GdJDP
打开压缩包得到flag.crypto
题目贴心的给了解密软件,得到flag
RE
1,oooollvm
其实这题我连混淆都没去~
本来看到ollvm,第一反应是想用deflat去的,结果总有几个流程算不清,就一直没再看,快结束了时候想起来看了看

这十分可疑啊
table1=[‘0x31‘,‘0x0E‘,‘0x10‘,‘0x38‘,‘0x06‘,‘0xA1‘,‘0x64‘,‘0x26‘,‘0x04‘,‘0x36‘,‘0xC1‘,‘0x2B‘,‘0xA4‘,‘0x07‘,‘0x7C‘,‘0x0C‘,‘0x94‘,‘0x06‘,‘0xC2‘,‘0x51‘,‘0xC4‘,‘0x01‘,‘0x4E‘,‘0xC1‘,‘0xB9‘,‘0x50‘,‘0xCE‘,‘0x8D‘,‘0xB1‘,‘0x45‘,‘0x44‘,‘0x9D‘,‘0x3F‘,‘0xA1‘]
table2=[‘0x59‘,‘0x68‘,‘0x73‘,‘0x56‘,‘0x6F‘,‘0xDD‘,‘0x25‘,‘0x61‘,‘0x40‘,‘0x69‘,‘0xA6‘,‘0x69‘,‘0xD9‘,‘0x47‘,‘0xD5‘,‘0x78‘,‘0xCB‘,‘0x7A‘,‘0xA4‘,‘0x28‘,‘0xBD‘,‘0x6E‘,‘0x4F‘,‘0xBA‘,‘0xA4‘,‘0x3D‘,‘0xB6‘,‘0xFB‘,‘0xEC‘,‘0x2F‘,‘0x12‘,‘0xF0‘,‘0x1A‘,‘0xBF‘]
for i in range(len(table1)):
table1[i]=int(table1[i],16)
table2[i]=int(table2[i],16)
for i in range(len(table2)):
for s in range(30,127):
if((~s & (table1[i]+i) | ~(table1[i]+i) & s)==table2[i]):
print(chr(s),end=‘‘)
continue
得到flag
以上是关于[Week 19]每日一题(C++,数学,并查集,动态规划)的主要内容,如果未能解决你的问题,请参考以下文章