算法设计与分析期中复习
Posted 咸鱼的小世界
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法设计与分析期中复习相关的知识,希望对你有一定的参考价值。
一、概论
什么是算法?
算法是求解问题的一系列步骤,用来将输入数据转换成输出结果

算法设计应该满足以下目标(对使用算法的人来讲)
- 正确性:算法能正确地执行,能完成任务
- 可使用性:算法要能被方便地使用
- 可读性:算法应具有较好的可读性,易于理解
- 健壮性:要有异常处理,对不合理的数据进行检查,从而避免异常中断或死机
- 高效率与低存储量需求:低时间复杂度,低空间复杂度。二者往往不可得兼
算法的五个特征(对设计算法的人来讲)
- 有限性:算法的的执行步骤是有限的,每个步骤都在有限时间内完成,即算法可在有限时间内被只执行完成
- 确定性:算法中每一条指令都有确切的含义,没有二义性(例:取出数组中差不多大的数,取出数组中最大的数)
- 可行性:算法的每个步骤都是可实现的,例如:整数乘法操作可用加法运算实现,乘2操作可用移位运算实现(表达算法中的操作可以被实现,对计算机而言,要有对应的指令,对人而言,要有步骤,纸,笔)
- 输入性:0个或多个
- 输出性:1个或多个
【例1.2】有下面两段描述,它们违反了算法的哪些特征?

答:第一段代码是一个死循环,违反了算法的有限性。第二段出现了零除错误,违法了算法的可行性。
算法的描述
以设计求1+2+…+n的值的算法为例说明C/C++语言描述算法的一般形式

在设计算法时,如果某个形参需要将执行结果回传给实参,需要将该形参设计为引用型参数。
算法与数据结构
- 算法+数据结构=程序(Niklaus Emil Wirth, 1934-)
- 联系:数据结构是算法设计的基础。算法的操作对象是数据结构,在设计算法时,通常要构建适合这种算法的数据结构。数据结构设计主要是选择数据的存储方式,如确定求解问题中的数据采用数组存储还是采用链表存储等。算法设计就是在选定的存储结构上设计一个满足要求的好算法。
- 区别:数据结构关注的是数据的逻辑结构、存储结构以及基本操作,而算法更多的是关注如何在数据结构的基础上解决实际问题。算法是编程思想,数据结构则是这些思想的逻辑基础。
算法分析
算法分析是分析算法占用计算机资源的情况。
算法分析的两个主要方面是分析算法的时间复杂度和空间复杂度。
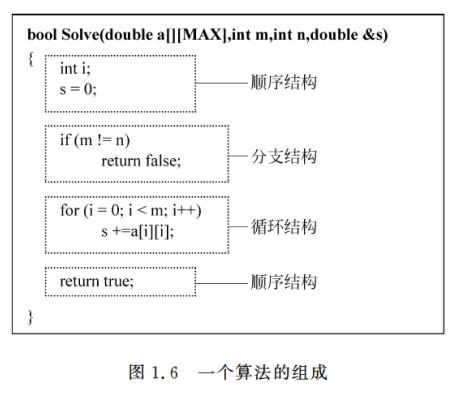
非递归算法时间复杂度分析
- 符号:
- 上界:O(n)(主要用这个)
- 下界:Ω(n)
- 同阶:
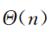
- 计算
- 大吞小,常系数删掉
- O(3n+2)=O(3n)=O(n)
- O(6n2+3n+2)=O(6n2+3n)=O(6n2)=O(n2)
- O(1):常数时间复杂度,即算法执行时间不会随着问题规模的增大而增大
- 【例1.3】分析以下算法的时间复杂度
void fun(int n) int s=0,i,j,k; for (i=0;i<=n;i++) for (j=0;j<=i;j++) for (k=0;k<j;k++) s++;
补充:对该问题而言,有几层for循环就是n的几次方,如果再加一层for循环for(l=0;l<k;i++),则时间复杂度为O(n4)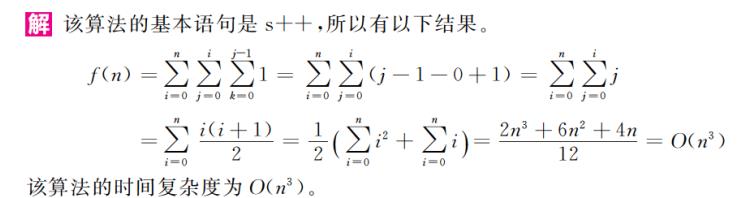
- 算法的三种情况
- 最好:算法基本语句执行的最小次数
- 最坏:算法基本语句执行的最大次数
- 平均:各种特定输入下的基本语句执行次数的带权平均值

递归算法时间复杂度分析
递归算法是采用一种分而治之的方法,把一个“大问题”分解为若干个相似的“小问题”来求解。
对递归算法时间复杂度的分析,关键是根据递归过程建立递推关系式,然后求解这个递推关系式,得到一个表示算法执行时间的表达式,最后用渐进符号来表示这个表达式即得到算法的时间复杂度。


非递归算法空间复杂度分析
临时空间随着算法的执行能增大多快
若所需临时空间相对于输入数据量来说是常数,则称此算法为原地工作或就地工作算法。若所需临时空间依赖于特定的输入,则通常按最坏情况来考虑。

非递归算法中如果有循环,则要注意在循环过程中是否申请了新的空间(malloc,new),非递归算法的时间复杂度不一定是O(1)
递归算法空间复杂度分析



算法设计工具-STL
随用随查,先省略
二、递归
三、分治
四、蛮力
五、回溯
六、分支限界
参考书
《算法设计与分析(第2版)》 李春葆 ISBN:9787302500988
算法设计与分析期中考试复习:代码和经典题目 分治二分动态规划(未完待续)
写在前面
自用的抱佛脚笔记。
代码可能跟书上不一样。
期中考试的范围:分治法和动态规划。
我的复习范围:
分治:快速排序,归并排序,二分查找,二分模板题(如派)。
动态规划:矩阵相乘,数塔,最长公共子序列,0-1背包。
快速排序
思想:
在数组a中找一个中枢元素x,用两个指针ij遍历数组:i从左往右,j从右往左;一开始i++,当出现a[i]>=x,i停止;j- -,当出现a[j]<=x时,j停止。
此时a[i]>=x,a[j]<=x,而我们需要的是x左边的数小于等于它,x右边的数大于等于它,因此swap(a[i],a[j]),继续执行i++,知道ij相遇。
排完一次之后x左边的数小于等于x,右边的数大于等于x;于是分别对x左边和右边进行快速排序。
#include<bits/stdc++.h>
using namespace std;
int n;
int a[200000+10];
void quick_sort(int l,int r)
{
if(l>=r) return;
int t=(l+r)/2;
int x=a[t];int i=l-1,j=r+1;
while(i<j)
{
do i++;while(a[i]<x);
do j--;while(a[j]>x);
if(i<j)swap(a[i],a[j]);//!!!一定要加if条件
}
quick_sort(l,j);
quick_sort(j+1,r);
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
quick_sort(1,n);
for(int i=1;i<=n;i++) cout<<a[i]<<" ";
return 0;
}
P1177 【模板】快速排序,可以在这里看看自己的快排模板写对没
归并排序
思想:
先一直分治,分到最小。然后开始排序。
取中点mid,由于前面的递归可知,mid左边和mid右边局部有序。
令i从l开始,j从mid+1开始,比较ij哪个小,小的放在新的数组里并指针往前移。
但凡有一个指针走完(i=mid或j=r),break;
则剩下的都是大的,直接接在新数组后。
然后新数组对旧数组赋值即可。
#include<bits/stdc++.h>
using namespace std;
int n;
int a[200000+10],b[200000+10];
void Merge_sort(int l,int r)
{
if(l>=r) return;
int mid=(l+r)/2;
Merge_sort(l,mid);
Merge_sort(mid+1,r);
int i=l,j=mid+1;
int k=0;
while(i<=mid&&j<=r)
{
if(a[i]<=a[j]) b[k++]=a[i++];
else b[k++]=a[j++];
}
while(i<=mid) b[k++]=a[i++];
while(j<=r) b[k++]=a[j++];
for(int ii=l,kk=0;ii<=r;ii++,kk++)
{
a[ii]=b[kk];
}
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
Merge_sort(1,n);
for(int i=1;i<=n;i++) cout<<a[i]<<" ";
return 0;
}
依旧可以通过提交上面的模板题以判断自己写对没。
二分
一般l和r分为这两种(非浮点):
r=mid,l=mid+1;
l=mid,r=mid-1;//那么mid=(l+r+1),否则容易死循环
#include<iostream>
#include<math.h>
using namespace std;
const int N=1e4+10;
int n,f;
double a[N];
const double pi=acos(-1.0);
double sum=0;
double eps=1e-5;
int judge(double mid)
{
int flag=0;
for(int i=1;i<=n;i++)
{
if(a[i]>=mid)
{
flag+=a[i]/mid;
}
}
if(flag>=f) return 1;
else return 0;
}
int main()
{
int t;cin>>t;
while(t--)
{
cin>>n>>f;
f++;
sum=0;
for(int i=1;i<=n;i++)
{
int t;cin>>t;
a[i]=pi*t*t;
sum+=a[i];
}
double l=0,r=sum,mid;
while(r-l>eps)
{
mid=(l+r)/2;
if(judge(mid)) l=mid;
else r=mid;
}
cout.precision(3);
cout<<fixed<<mid<<endl;
}
}
矩阵相乘
困了,明天再说。
偷懒的函数
快排:sort()
二分查找:lower_bound(a,a+n,x),返回第一个大于等于x的地址,想知道位置就要减去a
以上是关于算法设计与分析期中复习的主要内容,如果未能解决你的问题,请参考以下文章