Python_ML_19_隐马尔科夫模型
Posted tlfox2006
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python_ML_19_隐马尔科夫模型相关的知识,希望对你有一定的参考价值。
总结:
1. HMM的概念:
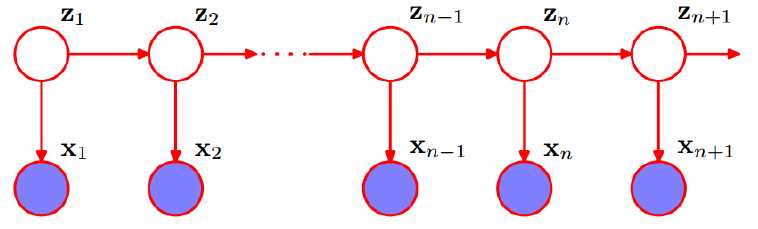
- {Z}是状态序列的随机变量,{x}是观测序列的随机变量,他们是随机变量。
- Q是状态集合,即气压集合(L,M,H),V是观测集合,即天气集合(S,C,W,R)
- I是状态序列,即气压序列(M,M,H,H,LL....),随机的但相互关联;A为转移矩阵:aij=P(it+1=qj|it=qt),即在前一刻的状态已知的情况下,这时刻的状态的概率。
- O是观测序列,即天气序列(W,C,S,S,R,C....),他们看似独立,其实相关,B是发射矩阵(触发状态,而得到观测序列的矩阵):bik=P(ot=vk|it=qi),即 t 时刻(当前时刻)的状态,激发出 t 时刻(当前时刻)的观测值的概率。如同,此时的状态是L(低气压),激发出此时的观测值R(下雨)。
- 而π是初始状态概率向量。
2. HMM两个性质
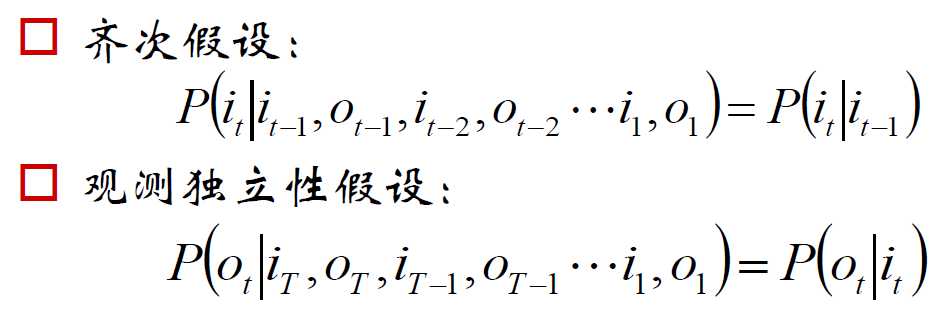
HMM的两个性质:
- 齐次假设:当期的状态与前多时刻的状态无关,只与前一期时刻的状态相关,即it只与it-1相关。(隐变量之间是不相关的)
- 观测独立假设:每期的输出值是由当期的状态所触发的,所以当前的输出值只与当期的状态有关,与前期的状态无关。
HMM直接计算:
HMM模型就是想得到P(O|λ),其实就是O和i的联合概率对所有I的求和:ΣP(O,I|λ),(边缘概率:联合概率对I求和就可以得到另一个变量的边缘概率),利用贝叶斯公式,P(O,I|λ) = P(O|I,λ) P(I|λ)。
P(O|I,λ) = P(O1,O2,...OT|i1,i2,..,iT; λ) --观测独立性假设(每期的输出值是由当期的状态所触发的,所以当前的输出值只与当期的状态有关,与前期的状态无关。)--> P(O1|i1;λ)*P(O2|i2;λ)*...* P(Ot|it;λ),其中P(O1|i1;λ)表示在i1这个状态时的观测值是O1,也是B11,以此类推得到B11....BTT。
P(I|λ) = P(i1,i2,..,iT | λ) = P(i1 | λ) * P(i2 | i1λ) * P(i3 | i2i1λ) *....* P(iT | iT-1.....i2i1λ) -- 齐次假设(当期的状态与前多时刻的i无关,只与前一期时刻的状态相关)--> =P(i1 | λ) * P(i2 | i1λ) * P(i3 | i2i1λ) *....* P(iT | iT-1.....i2i1λ)
而π1就是初始时,能够观测的 i1 隐状态的概率,即P(i1 | λ)。
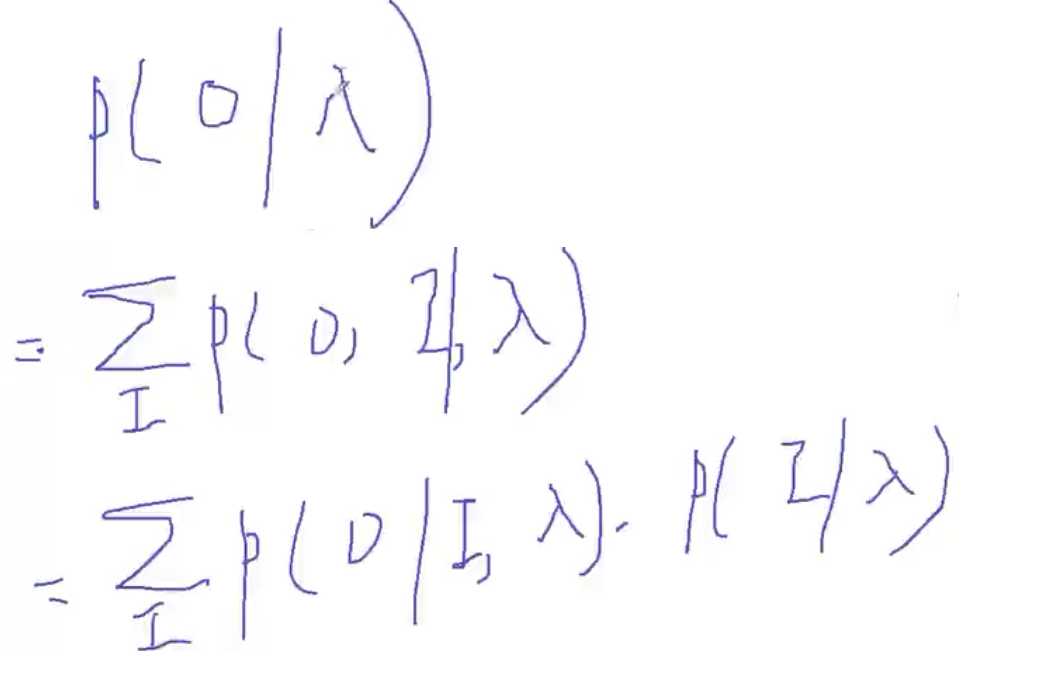
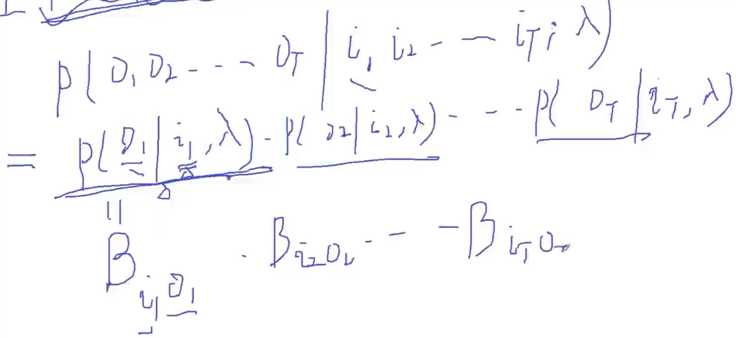
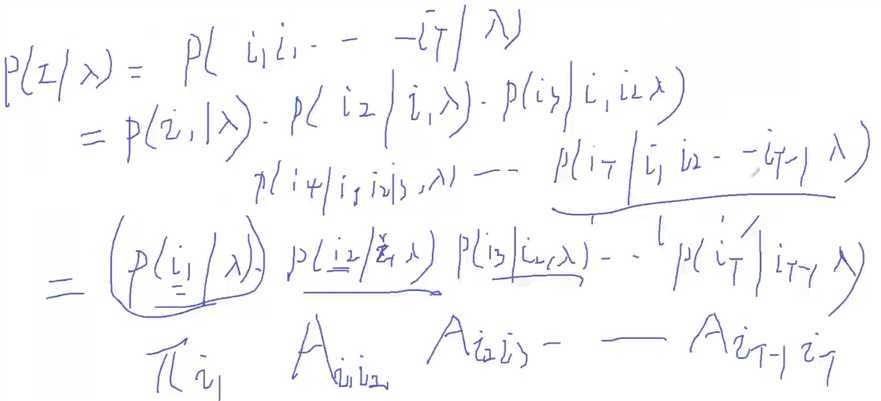
正文

隐马尔科夫是一个特别有用的概念,在目标跟踪或滤波中广泛使用的卡尔曼滤波就是一个隐马尔科夫的应用,还有好多好多别的应用。当z是离散的,它就是HMM, 而当z连续的,它就变成了卡尔曼滤波。
马尔科夫(有时又称为可视马尔科夫,VMM)与隐马尔科夫(HMM)都是用来描述时序概率问题的,用当前及过去的信息来预测未来信息。那么VMM与HMM有什么区别呢,VMM中的状态序列是可观测的,HMM中的状态序列是不可观测的,而可观测到的事件是一个状态序列的一个概率事件,即HMM是一个双重随机过程,其中的状态转移是隐藏的,所以称为隐马尔科夫。
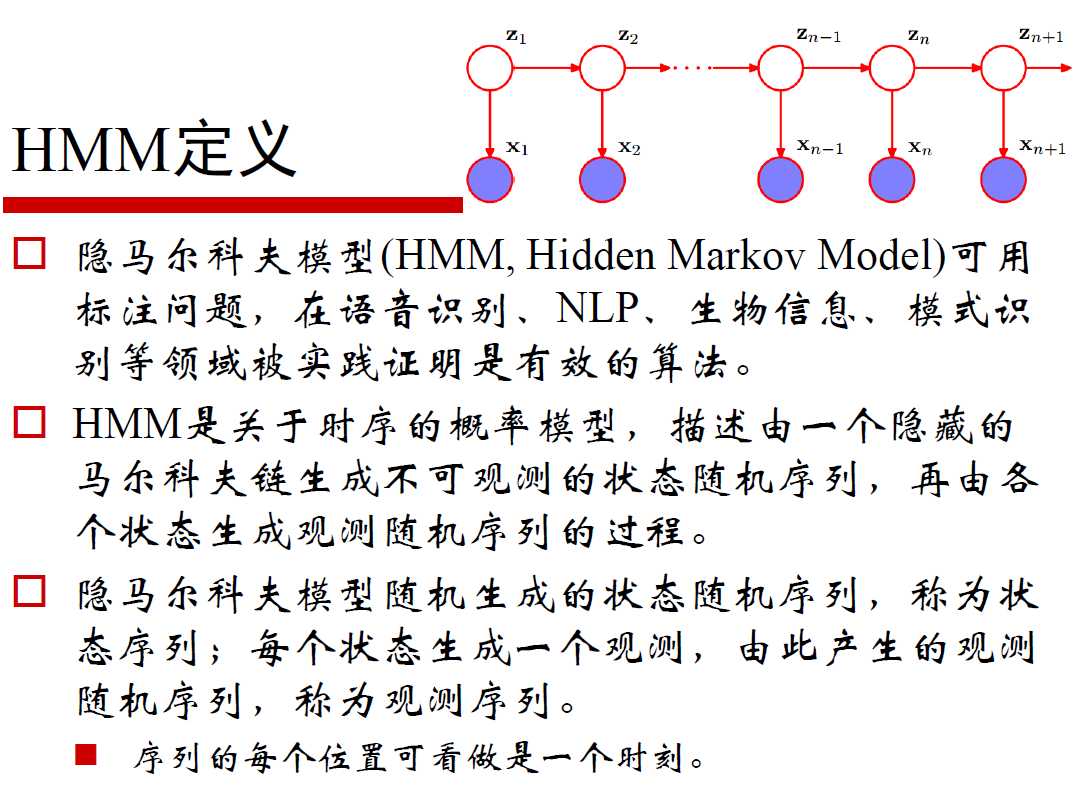
隐马尔科夫模型是关于时序的概率模型,描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列(称为状态序列),再由状态随机序列生成观测随机序列的过程(称为观测序列)。
HMM是一个时间序列的模型,专门做时间/空间序列的数据做分析,其样本之间并不独立,我们之前所做的所有算法都是假定样本是独立的,认为样本之间没有相关性。
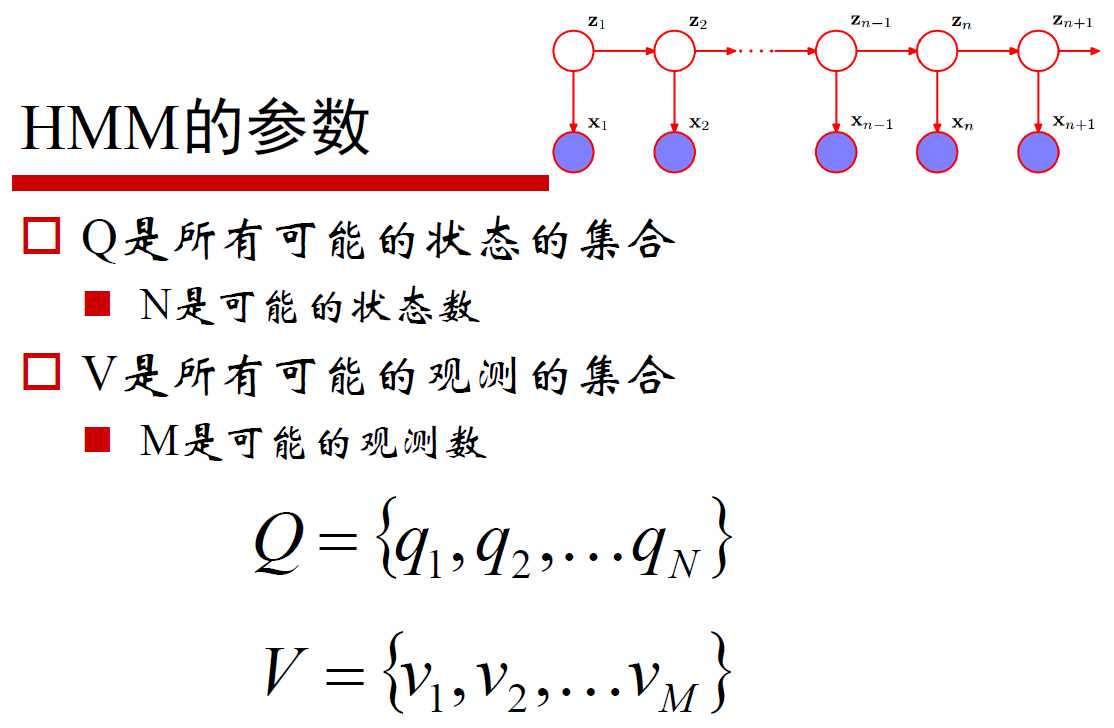

Q是状态集合,即气压集合(L,M,H),V是观测集合,即天气集合(S,C,W,R)
I是状态序列,即气压序列(M,M,H,H,LL....),随机的但相互关联;A为转移矩阵:aij=P(it+1=qj|it=qt),即前一刻的状态的情况下,这时刻的状态的概率。
O是观测序列,即天气序列(W,C,S,S,R,C....),他们看似独立,其实相关,B是发射矩阵(触发状态,而得到观测序列的矩阵):bik=P(ot=vk|it=qi),即t时刻的状态,激发出t时刻的观测值的概率。如同,此时的状态是L(低气压),激发出此时的观测值R(下雨)。


时间序列的例子:天气(sunny,cloudy,windy,raining),昨天的x1会对今天的x2又直接的关联,今天x2又会对明天x3有所关联,直到xn。若给定了第i天的天气,那么在xi已知的情况下,xi-1和xi+1的联合概率等他们条件概率分别的乘积: P(xi-1,xi+1|xi) = P(xi-1|xi) * P(xi+1|xi),这就叫马尔科夫模型。
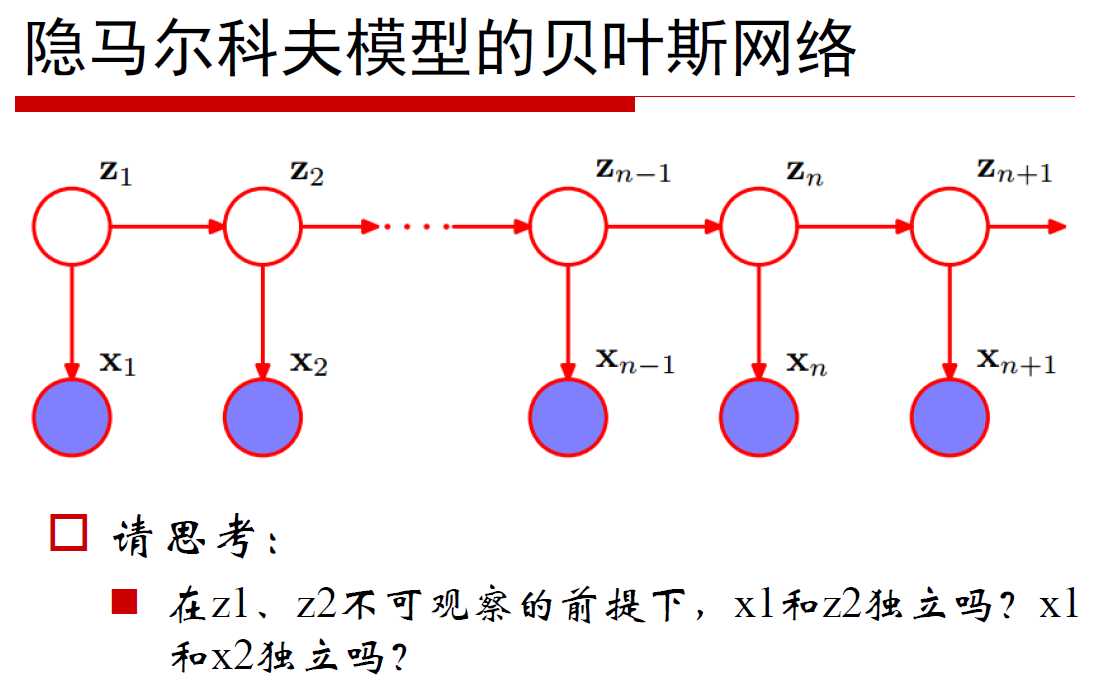
我们又已知的一系列观测值x1,x2,..xn(天气:S,C,W,R),而它有一系列隐含数据z1,z2,...,zn,(假设{z}是气压:L,M,H,无法直接观察到的隐变量),这些隐含数据我们是观察不到的,但他们之间是相互关联,并对观测数据{x}会产生直接的影响。
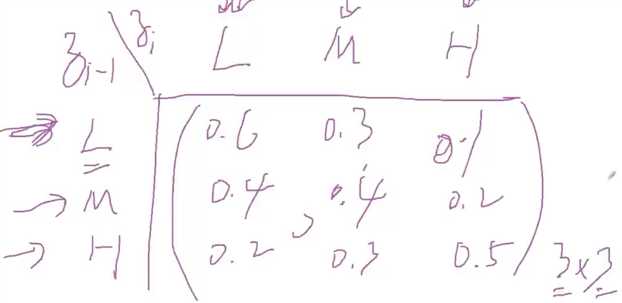
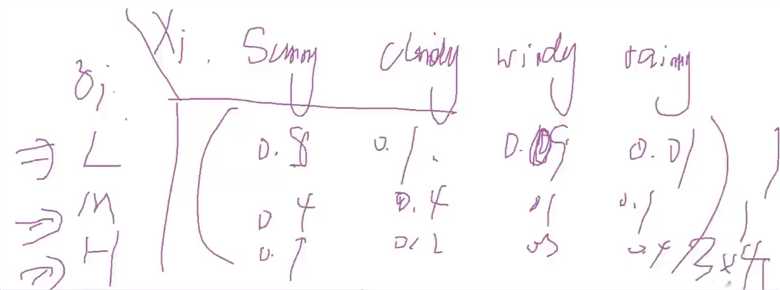
隐含变量之间的关系的状态转化矩阵,zi-1指前天的气压值,zi是今天的气压值,前一天 zi-1 是低气压,今天zi 是L,M,H的概率分别是0.6,0.3,0.1. 类似地,每行都是在前一天的气压已知的情况下,今天的气压式什么的概率(条件概率)。前一天zi-1 的气压值都会对今天的气压值的转化概率,他是条件概率,所以每一行相加都是1. 我们称这个矩阵为状态转移矩阵,如果观察的集合是V,它的个数是n的话,那么这个转移矩阵就是Anxn。
而z对x影响的矩阵称为发射矩阵或混淆矩阵,它是Bnxm的矩阵(n是z可观察样本的个数,m是x可观察样本的个数)。
π是HMM的初始化向量,则λ=(A,B,π)就是HMM的所有参数。

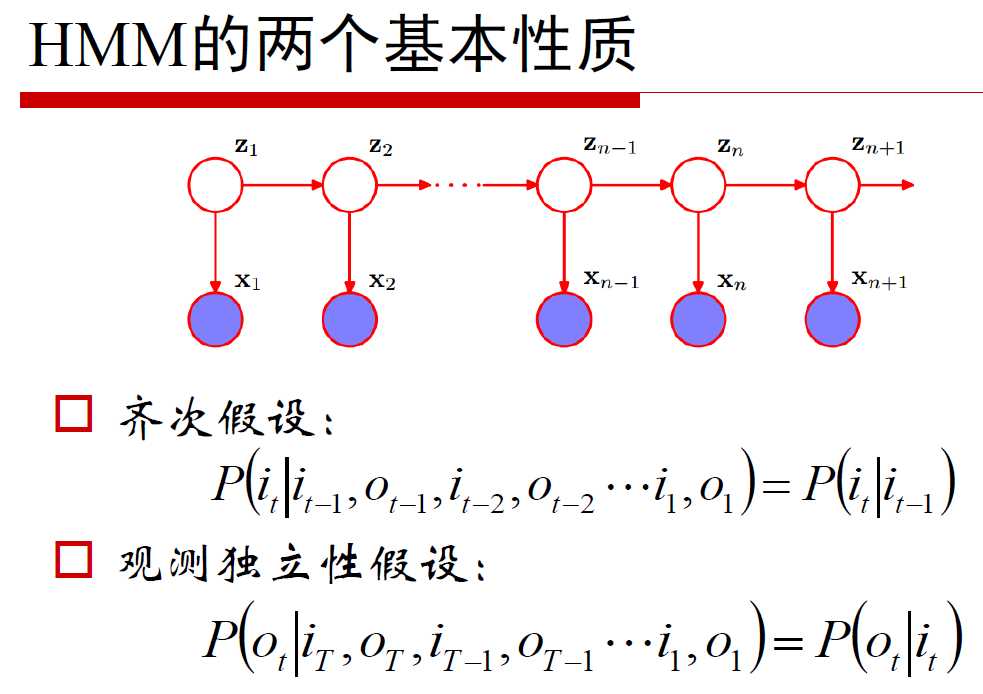
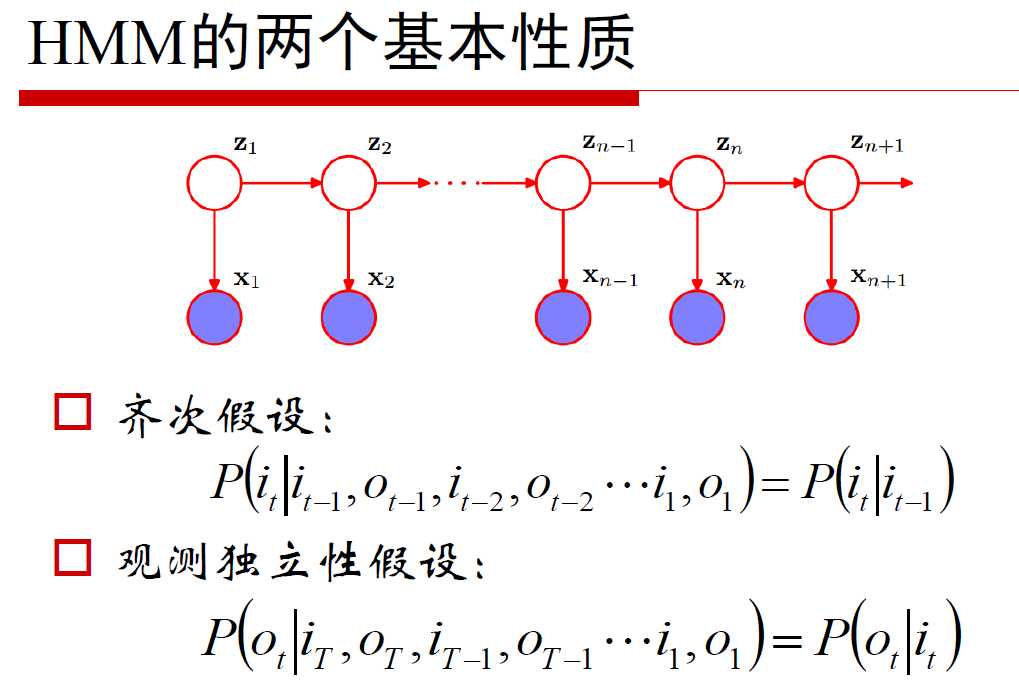
HMM的两个性质:
- 齐次假设:当期的状态与前多时刻的状态无关,只与前一期时刻的状态相关,即it只与it-1相关。
- 观测独立假设:每期的输出值是由当期的状态所触发的。
HMM举例


A是状态矩阵,是状态之间转化得矩阵,一般是未知的,通过计算等到。aij=P(it+1=qj|it=qt)
B是发射矩阵,是用来触发状态,得到观测的矩阵:bik=P(ot=vk|it=qi)



我们想得到P(O|λ),其实就是O和i的联合概率对所有I的求和:ΣP(O,I|λ),(边缘概率:联合概率对I求和就可以得到另一个变量的边缘概率),利用贝叶斯公式,P(O,I|λ) = P(O|I,λ) P(I|λ)。
P(O|I,λ) = P(O1,O2,...OT|i1,i2,..,iT; λ) --观测独立性假设(每期的输出值是由当期的状态所触发的,所以当前的输出值只与当期的状态有关,与前期的状态无关。)--> P(O1|i1;λ)*P(O2|i2;λ)*...* P(Ot|it;λ),其中P(O1|i1;λ)表示在i1这个状态时的观测值是O1,也是B11,以此类推得到B11....BTT。
P(I|λ) = P(i1,i2,..,iT | λ) = P(i1 | λ) * P(i2 | i1λ) * P(i3 | i2i1λ) *....* P(iT | iT-1.....i2i1λ) -- 齐次假设(当期的状态与前多时刻的i无关,只与前一期时刻的状态相关)--> =P(i1 | λ) * P(i2 | i1λ) * P(i3 | i2i1λ) *....* P(iT | iT-1.....i2i1λ)
而π1就是初始时,能够观测的 i1 隐状态的概率,即P(i1 | λ)。
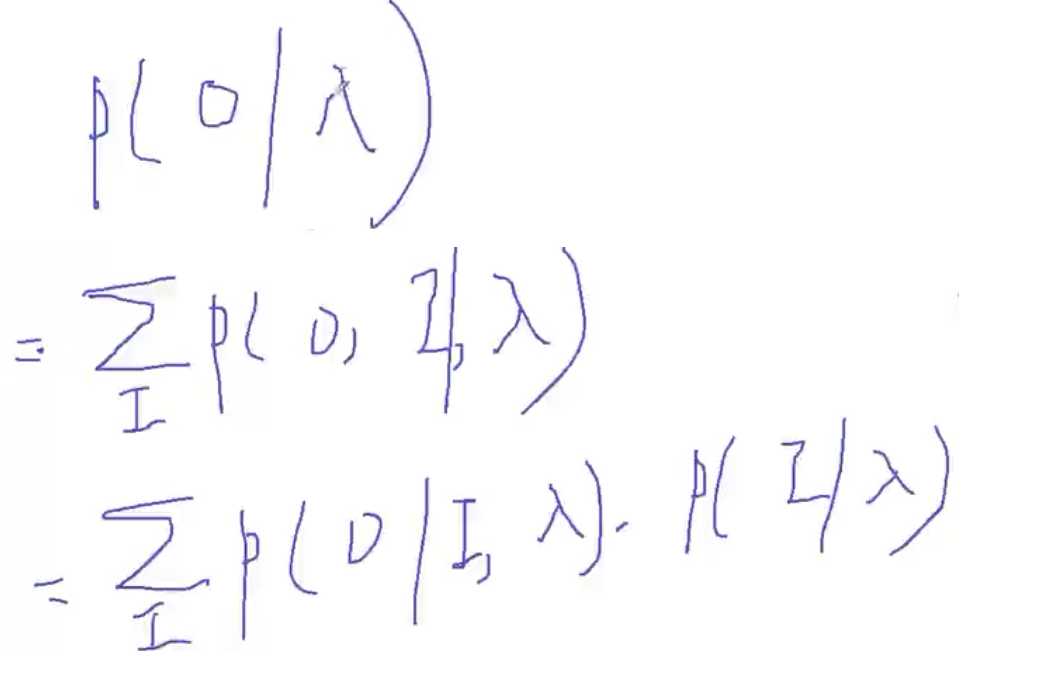
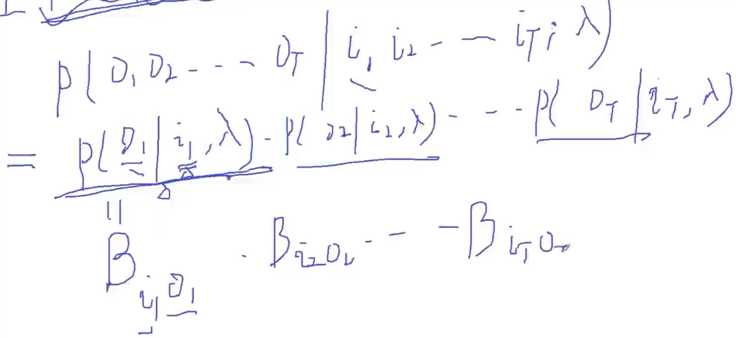
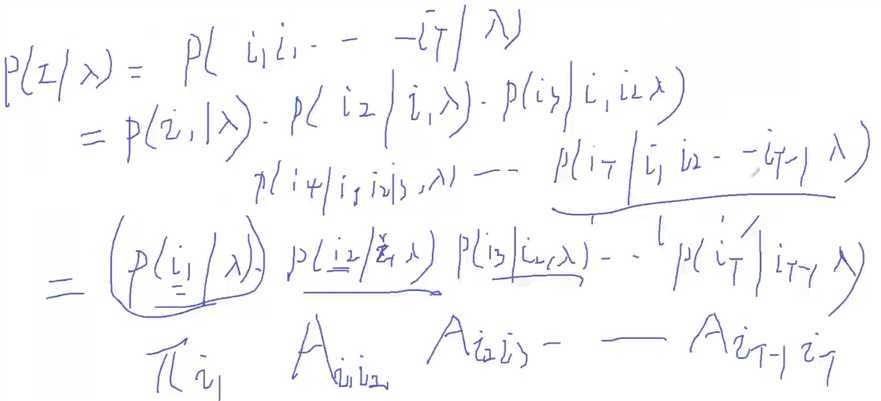
以上是关于Python_ML_19_隐马尔科夫模型的主要内容,如果未能解决你的问题,请参考以下文章