m基于整数序列的QC-LDPC的稀疏校验矩阵构造算法性能对比matlab仿真,对比差分序列,PEG,Mackey等

Posted 2023-05-04 51matlab

1.算法仿真效果

matlab2013b仿真结果如下：

 

 

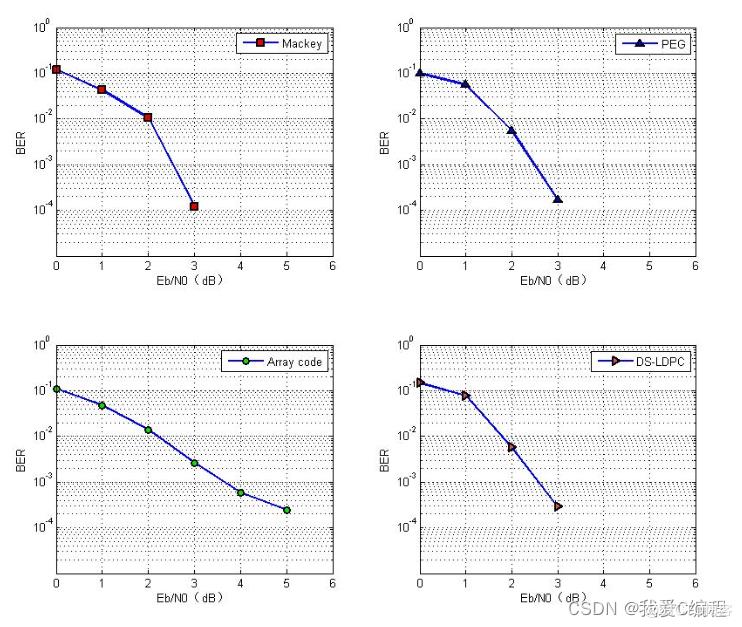
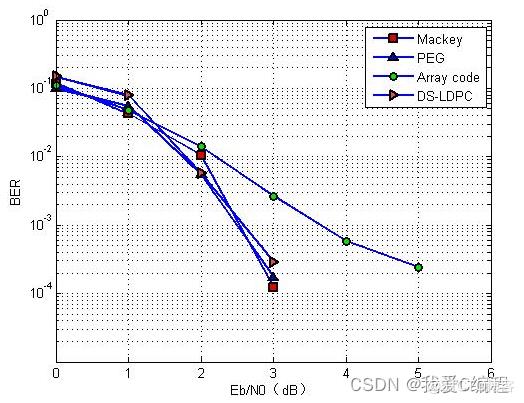
2.算法涉及理论知识概要

       QC-LDPC（Quasi-Cyslic Low-Density Parity-Check Codes）即准循环LDPC码。之前介绍的LDPC码基本属于随机构造法，构造出的码性能很好，但校验矩阵具有不规律性，存在校验矩阵存储于读取困难、编码复杂度高等问题，相对难以实现。准循环LDPC码是结构化LDPC码的重要子集，其奇偶校验矩阵可以分成多个大小相等的方阵，每个方阵都是单位矩阵的循环移位矩阵或全0矩阵，非常便于存储器的存储和寻址，从而大大降低了LDPC码的编译码复杂度，并且具有重复累计结构的准循环LDPC码能够实现线性复杂度的快速编码。因此，目前实际中所使用的LDPC码大都使用这种校验矩阵构造方式。

 

        LDPC码是一种处于发展中的信道编码，其性能优异，具体表现为：描述简单， 硬件实现复杂度低，译码复杂度较低，可以实现完全的并行操作，且具有较低的 译码错误平台。另外，码在信道条件较差的无线移动通信系统中 展现出了巨大的应用前景，非常适用于未来的移动通信系统。因此，码的 研究、实现及应用是纠错编码领域中的一个热点课题，倍受学术界和工业界的重 视和关注。

        目前，码已经不再局限于理论的研究，正逐步转变到商业应用中。作为 深空通信的编码标准，码早已在美国宇航局中体现了自身的价值。 现如今码信道编码方案己应用到多种通信标准，例如，无线局域网、 宽带无线接入协议也称、中国数字电视地面广播标准、中国移动多媒体广播以及欧洲数字电视广播卫星标准 等都采纳了码。另外，码还广泛地应用于光通信、光和磁记录系统以 及混合自动请求重传设计等领域。

 

　　LDPC 码早于1962 年由Gallager提出，可以看成是一个具有稀疏校验矩阵的线性分组码。自从Mackay 和Neal发现LDPC 码的性能非常接近香农限以后，LDPC 码越来越受到人们的重视。基于准循环LDPC（QC-LDPC）码结构特点，提出了一种支持多种码率QC-LDPC 译码器的设计方法，并设计实现了一个能够实时自适应支持三个不同H 阵的通用QC-LDPC 译码器。

 

　　1 QC-LDPC 码简介

 

　　QC-LDPC 码的校验矩阵Hqc 是由c × t 个循环置换矩阵组成的，其中c，t均为整数，且c < t 。将QC-LDPC码的校验矩阵中每一个置换矩阵替换为相应的移位值，这样得到了一个新的矩阵，称为基本矩阵。基本矩阵与Η 阵是一一对应的。QC-LDPC 规则的结构使得其编译码在工程上易于实现，因此许多标准中的LDPC 码都采用了QC-LDPC 码。

 

　　2 译码算法简介

 

　　这里设计的译码器主要采用基于软判决的偏移值和算法。偏移值和算法是在和积算法和和算法的基础上改进而来，具有译码复杂度低，性能优异等特点。为了能够较好地描述该算法，先对一些符号进行定义。

 

 

 

        具有代数结构的码是解决实际应用中存储问题的良好候 选码。在本章中，基于一种组合设计，即差分序列，我们设计了一类 码，称为码。同时，考虑到相对大的围长能够提升码字的误码性能， 给出了一种查找好的差分序列以保证码的围长至少为的搜索算 法。

 

         接下来，介绍一类，码，称为码。这类码的奇偶校验 矩阵是由二次多项式产生的零阶、一阶和二阶差分序列组成，其奇偶校验矩阵的 构造过程总结如下：

 

 

 

 

 

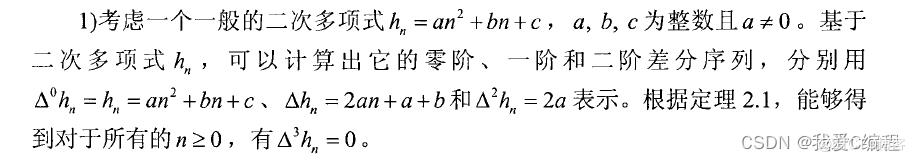
3.MATLAB核心程序

 

R        = 0.5;%设置码率为1/2；
N        = 402;%设置奇偶校验矩阵大小     
M        = N*R;
EbN0     = 0:1:3;     %设置Eb/N0；*
lends    = [1000,500,400,300,200,100]/2;
Max_iter = 50;               %最大迭代次数*
%产生奇偶校验矩阵
H        = mackay(M,N);
for i=1:length(EbN0)
    i
    Bit_err(i)    = 0; %设置误码率参数
    Num_err       = 0; %蒙特卡洛模拟次数
    Numbers       = 0; %误码率累加器
    iter_moy_temp = [];%叠加寄存器
    while Num_err <= lends(i)       
        fprintf(\'Eb/N0 = %f\\n\', EbN0(i));
        Num_err
        Trans_data           = round(rand(N-M,1));           %产生需要发送的随机数
        [ldpc_code,newH]     = func_Enc(Trans_data,H);       %LDPC编码
        u                    = [ldpc_code;Trans_data];       %LDPC编码
        Trans_BPSK           = 2*u-1;                        %BPSK
        %通过高斯信道
        N0                   = 2*10^(-EbN0(i)/10);
        Rec_BPSK             = Trans_BPSK+sqrt(N0/2)*randn(size(Trans_BPSK));
        %LDPC译码 
        [vhat,nb_iter]       = func_Dec(Rec_BPSK,newH,N0,Max_iter);
        iter_moy_temp(end+1) = nb_iter;
        
        [nberr,rat]          = biterr(vhat\',u);
        Num_err              = Num_err+nberr;
        Numbers              = Numbers+1;
    end
    Bit_err(i) = Num_err/(N*Numbers);
end
figure;
semilogy(EbN0,Bit_err,\'o-\');
xlabel(\'Eb/N0（dB）\');
ylabel(\'BER\');
grid on;
save ldpc_mackey.mat EbN0 Bit_err

 

　　

 

避免使用 Eigen 分解稀疏矩阵时的动态内存分配

【中文标题】避免使用 Eigen 分解稀疏矩阵时的动态内存分配

【英文标题】：Avoiding dynamic memory allocation on factorizing sparse matrix with Eigen

【发布时间】：2020-07-17 12:28:15

【问题描述】：

在我的应用程序中，除了类构造函数之外，我需要避免动态内存分配（类似 malloc）。 我有一个稀疏的半定矩阵 M，它的元素在程序执行期间会发生变化，但它具有固定的稀疏模式。

为了尽可能快地求解许多线性系统 M * x = b，想法是在我的类构造函数中使用 inplace 分解，如Inplace matrix decompositions 中所述，然后在任何时候调用 factorize 方法M 变化：

struct MyClass 
private:
    SparseMatrix<double> As_;
    SimplicialLDLT<Ref<SparseMatrix<double>>> solver_;
public:
    /** Constructor */
    MyClass( const SparseMatrix<double> &As ) 
        : As_( As )
        , solver_( As_ ) // Inplace decomposition
    

    void assign( const SparseMatrix<double> &As_new ) 
        // Here As_new has the same sparsity pattern of As_
        solver_.factorize( As_new );
    

    void solve( const VectorXd &b, VectorXd &x )
    
        x = solver_.solve( b );
    

然而，factorize 方法仍然会创建一个与 As_ 大小相同的临时文件，因此使用动态内存分配。

是否有可能以某种方式避免它？如果 Eigen API 不允许此功能，一个想法是创建 SimplicialLDLT 的派生类，以便仅在将在类构造函数中调用的 analyzePattern 方法中执行动态内存分配。欢迎提出建议...

【问题讨论】：

恐怕如果不对稀疏求解器逻辑进行几次更改，这是不可能的（最重要的是，您需要一种方法来在多个步骤中继续为临时对象重用内存）。不过，我必须再次检查来源以获得明确的答案。

如果有机会我可以在派生类中实现此功能。我认为它对于嵌入式和实时应用程序非常有用，在这些应用程序中，动态内存分配通常只允许在启动阶段进行。

另一种可能的解决方案是将自定义分配器添加到求解器构造函数。应该动态分配的临时矩阵和向量从分配器中检索内存。实时系统的分配器可以由固定大小的内存池表示。这种策略在其他情况下也很有用。

分析 SimplicialCholesky.h 可以避免使用 Upper 三角形部分和 NaturalOrdering 进行动态分配。准确地说，第一次调用 factorize 方法仍然是动态分配内存，但可以在 ctor 类中完成。关于排序，可以手动调用 ordering 方法（在 ctor 中），如link 所述，注意将排列应用于 rhs 和解决方案向量。唯一值得关注的是文档中的指示此模块目前仅供内部使用。

这个想法部分有效：使用 NaturalOrdering 防止因式分解方法分配内存。另一方面，我需要在运行 factorize 方法之前手动置换输入矩阵，即：H.selfadjointView<Upper>() = As_new.selfadjointView<Upper>().twistedBy(P); 它会创建临时对象。有什么建议可以避免吗？

【参考方案1】：

最后我找到了使用 CSparse 库获取 H = P * A * P' 的解决方法：

class SparseLDLTLinearSolver 
private:
    /** Ordering algorithm */
    AMDOrdering<int> ordering_;
    /** Ordering P matrix */
    PermutationMatrix<Dynamic, Dynamic, int> P_;
    /** Inverse of P matrix */
    PermutationMatrix<Dynamic, Dynamic, int> P_inv_;
    /** Permuted matrix H = P * A * P' */
    SparseMatrix<double> H_;
    /** H matrix CSparse structure */
    cs H_cs_;
    /** Support vector for solve */
    VectorXd y_;
    /** Support permutation vector */
    VectorXi w_;
    /** LDLT sparse linear solver without ordering */
    SimplicialLDLT<SparseMatrix<double>, Upper, NaturalOrdering<int>> solver_;
public:
    int SparseLDLTLinearSolver( const SparseMatrix<double> &A )
        : P_( A.rows() )
        , P_inv_( A.rows() )
        , H_( A.rows(), A.rows() )
        , y_( A.rows() )
        , w_( A.rows() )
    
        assert( ( A.rows() == A.cols() ) && "Invalid matrix" );
        ordering_( A.selfadjointView<Upper>(), P_inv_ );
        P_ = P_inv_.inverse();
        H_ = A.triangularView<Upper>();
        H_.makeCompressed();
        // Fill CSparse structure
        H_cs_.nzmax = H_.nonZeros();
        H_cs_.m = H_.rows();
        H_cs_.n = H_.cols();
        H_cs_.p = H_.outerIndexPtr();
        H_cs_.i = H_.innerIndexPtr();
        H_cs_.x = H_.valuePtr();
        H_cs_.nz = -1;
        const cs_sparse A_cs
            A.nonZeros(), A.rows(), A.cols(),
            const_cast<int*>( A.outerIndexPtr() ),
            const_cast<int*>( A.innerIndexPtr() ),
            const_cast<double*>( A.valuePtr() ),
            -1 ;
        cs_symperm_noalloc( &A_cs, P_.indices().data(), &H_cs_, w_.data() );
        solver_.analyzePattern( H_ );
        // Factorize in order to allocate internal data and avoid it on next factorization
        solver_.factorize( H_ );
        /*.*/
        return -solver_.info();
    

    int factorize( const Eigen::SparseMatrix<double> &A )
    
        assert( ( A.rows() == P_.size() ) && ( A.cols() == P_.size() ) &&
            "Invalid matrix size" );
        // Fill CSparse structure
        const cs_sparse A_cs 
            A.nonZeros(), A.rows(), A.cols(),
            const_cast<int*>( A.outerIndexPtr() ), 
            const_cast<int*>( A.innerIndexPtr() ), 
            const_cast<double*>( A.valuePtr() ), 
            -1 ;
        cs_symperm_noalloc( &A_cs, P_.indices().data(), &H_cs_, w_.data() );
        solver_.factorize( H_ );
        /*.*/
        return -solver_.info();
    

    void solve( const VectorXd &rhs, VectorXd &x )
    
        assert( ( rhs.size() == P_.size() ) && ( x.size() == P_.size() ) &&
            "Invalid vector size" );
        // Solve (P * A * P') * y = P * b, then return x = P' * y
        y_ = solver_.solve( P_ * rhs );
        x.noalias() = P_inv_ * y_;
    
;

cs_symperm_noalloc 是对 CSparse 库的 cs_symperm 函数的小重构。

它似乎有效，至少在我的特殊问题上。如果 Eigen 避免为一些稀疏矩阵运算创建临时变量（到堆中），那么在未来将非常有用。