随机造数据的技巧总结

Posted GOD-HJ

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了随机造数据的技巧总结相关的知识，希望对你有一定的参考价值。

以下是一个简单的使用 C++11 新特性生成随机数数据的程序示例：

#include <iostream>
#include <random>  // 引入随机数生成器的头文件
using namespace std;
int main()
    // 创建 C++11 随机数生成器
    mt19937_64 rng(std::random_device());
    // 使用随机数生成器创建均匀分布
    uniform_int_distribution<int> dist(0, 100);
    // 随机生成 10 个整数并输出它们
    for (int i = 0; i < 10; i++)
        int random_num = dist(rng);
        cout << random_num << " ";
    
    cout << endl;
    return 0;

这个程序用到了 C++11 的两个新特性：随机数生成器和随机分布。std::mt19937_64 是生成随机数的类，可以用 std::random_device 类来获取系统的随机种子，然后把它作为构造函数中的参数传给 std::mt19937_64 的对象来生成随机数。std::uniform_int_distribution<int> 则是一个随机的整数分布，它需要两个参数来构造一个均匀分布：分别是随机数的范围的最小值和最大值。

当然也可以用 rand() 函数生成随机数。但在C++11中已经有更加强大的随机数生成器（如上文），推荐使用更加先进的方式生成随机数。rand() 函数会使用计算机的时间作为随机种子，因此可能会存在一些问题，具体如下：

  1. rand() 可能不够随机：使用 rand() 接口会有产生伪随机数的风险，而 C++11 标准引入了更加随机的随机数生成器；

  2. rand() 生成随机数的范围受限：rand() 生成的随机数范围是 [0, RAND_MAX] ，而且计算 RAND_MAX 时，可能会限制随机数的分布均匀性。

下面是一个使用 rand() 函数生成区间内随机数的示例代码：

#include <iostream>
#include <cstdlib>   // 引入 srand() 和 rand() 函数
using namespace std;
signed main(void)
    const int kLowerBound = 1;  // 区间下限
    const int kUpperBound = 100;  // 区间上限
    const int kDataNum = 20;  // 需要生成的数据量

    // 设置种子
    srand(time(nullptr));
	//或者srand(time(NULL))也行，NULL换为0也可以。

    // 生成随机数
    int data[kDataNum];
    for (int i = 0; i < kDataNum; i++)
        data[i] = rand() % (kUpperBound - kLowerBound + 1) + kLowerBound;

    // 输出生成的数据
    for (int i = 0; i < kDataNum; i++)
        cout << data[i] << " ";
    cout << std::endl;
    return 0;

上述代码中，我们已经设置种子并使用 rand() 函数生成了区间 [1, 100] 内的随机数，并将它们存储在了一个数组（data）中。如果需要生成非整数的区间内的随机数，可以将 rand() % (kUpperBound - kLowerBound + 1) + kLowerBound 改为较为通用的式子 ((double) rand() / RAND_MAX) * (kUpperBound - kLowerBound) + kLowerBound。

总之，虽然在 C++11 引入的随机数库中有更先进、可靠、易用的随机数生成器，但是这里提供的方法仍然是缺乏更可靠性、更灵活性的解决方案之一。

上面的程序将生成 10 个 0 到 100 之间的随机整数并输出它们。你可以根据需要进行修改，例如改变随机数的范围或者将生成的随机数存储到一个数组中。

如果给定的得分表有特殊性质，例如排序好的、连续递增或递减的等，我们可以通过这些特殊性质来快速地生成多组数据。

以一个简单的例子来说明，如果给定的得分表是一个递增的数列，我们可以按照以下方式构造等多组数据：

  1. 随机生成一个数作为第一个数。
  2. 从第二个数开始，每个数比前一个数多增加若干个随机的增量，增量的大小可以根据需要自己设定，可以是一个固定的数，也可以是一个随机数。
  3. 重复第2步，直到生成需要的数据量。

以下是一个使用 C++ 的程序示例：

#include <iostream>
#include <random>  // 引入随机数生成器的头文件
using namespace std;
signed main(void)
    const int kDataNum = 10;  // 需要生成的数据量
    int data[kDataNum];  // 保存生成的数据的数组
    // 随机生成第一个数
    random_device rd;
    mt19937 gen(rd());
    uniform_int_distribution<> dis(0, 100);
    data[0] = dis(gen);
    // 生成后面的数
    uniform_int_distribution<> delta_dis(1, 10);  // 增量取 1 到 10 之间的随机数
    for (int i = 1; i < kDataNum; i++)
        data[i] = data[i - 1] + delta_dis(gen);
    // 输出生成的数据
    for (int i = 0; i < kDataNum; i++)
        cout << data[i] << " ";
    cout << endl;
    return 0;

这个程序将生成一个长度为 10 的递增数列，每个数之间的增量随机取 1 到 10 之间的整数。你可以根据需要修改随机数的范围和增量的大小来生成其他类型的数据。除了递增的数列外，类似的方式也可以用于递减数列、正负交替等有特殊性质的得分表。

下面以不同的得分表特殊性质为例，展示如何快速生成多组数据。

  1. 递增的得分表
#include <iostream>
#include <random>  // 引入随机数生成器的头文件
using namespace std;
signed main(void)
    const int kDataNum = 20;  // 需要生成的数据量
    int data[kDataNum];  // 保存生成的数据的数组
    // 随机生成第一个数
    random_device rd;
    mt19937 gen(rd());
    uniform_int_distribution<> dis(0, 100);
    data[0] = dis(gen);
    // 生成后面的数
    uniform_int_distribution<> delta_dis(1, 10);  // 增量取 1 到 10 之间的随机数
    for (int i = 1; i < kDataNum; i++)
        data[i] = data[i - 1] + delta_dis(gen);
    // 输出生成的数据
    for (int i = 0; i < kDataNum; i++)
        cout << data[i] << " ";
    cout << endl;
    return 0;
  1. 递减的得分表
#include <iostream>
#include <random>  // 引入随机数生成器的头文件
using namespace std;
signed main(void)
    const int kDataNum = 20;  // 需要生成的数据量
    int data[kDataNum];  // 保存生成的数据的数组
    // 随机生成第一个数
    random_device rd;
    mt19937 gen(rd());
    uniform_int_distribution<> dis(0, 100);
    data[0] = dis(gen);
    // 生成后面的数
    uniform_int_distribution<> delta_dis(1, 10);  // 减量取 1 到 10 之间的随机数
    for (int i = 1; i < kDataNum; i++)
        data[i] = data[i - 1] - delta_dis(gen);
    // 输出生成的数据
    for (int i = 0; i < kDataNum; i++)
        cout << data[i] << " ";
    cout << endl;
    return 0;
  1. 奇数偶数交替的得分表
#include <iostream>
#include <random>  // 引入随机数生成器的头文件
using namespace std;
signed main(void)
    const int kDataNum = 20;  // 需要生成的数据量
    int data[kDataNum];  // 保存生成的数据的数组
    // 随机生成第一个数
    random_device rd;
    mt19937 gen(rd());
    uniform_int_distribution<> dis(0, 100);
    data[0] = dis(gen) % 2;  // 取出第一个数的奇偶性
    // 生成后面的数
    uniform_int_distribution<> delta_dis(1, 10);  // 取 1 到 10 之间的随机数
    for (int i = 1; i < kDataNum; i++)
        data[i] = data[i - 1] + (i % 2 == 0 ? delta_dis(gen) : -delta_dis(gen));
    // 输出生成的数据
    for (int i = 0; i < kDataNum; i++)
    	cout << data[i] << " ";
    cout << endl;
    return 0;
  1. 以一定规律重复的得分表
#include <iostream>
using namespace std;
signed main()
    const int kDataNum = 20;  // 需要生成的数据量
    int data[kDataNum];  // 保存生成的数据的数组
    // 生成数据
    for (int i = 0; i < kDataNum; i++)
        data[i] = i % 3;  // 每3个数重复一次
    // 输出生成的数据
    for (int i = 0; i < kDataNum; i++)
        cout << data[i] << " ";
	cout<<endl;
	return 0;

也可以生成随机树，序列，图等。

下面是使用 std::mt19937_64 随机生成序列、树和图的示例代码：

  1. 随机生成序列
#include <iostream>
#include <vector>
#include <random>

int main()

    const int kDataNum = 20;
    std::random_device rd;
    std::mt19937_64 gen(rd());
    std::uniform_int_distribution<> dis(1, 100);
    std::vector<int> data(kDataNum);
    for (int i = 0; i < kDataNum; i++)
    
        data[i] = dis(gen);
    
    for (int i = 0; i < kDataNum; i++)
    
        std::cout << data[i] << " ";
    
    std::cout << std::endl;
    return 0;
  1. 随机生成树、图
    生成随机树的常用方法是随机生成一张图，然后选取一颗生成树。下面是使用C++的STL库中的std::mt19937_64生成随机图和随机树的示例代码：
#include <iostream>
#include <random>
#include <vector>
#include <algorithm>

const int N = 10; //图中节点数

int main() 
    std::mt19937_64 engstd::random_device();

    std::uniform_int_distribution<int> dist(0, N - 1); //生成随机整数分布

    //生成图
    std::vector<std::vector<int>> graph(N, std::vector<int>(N, 0));
    for (int i = 0; i < N; i++) 
        for (int j = 0; j < i; j++) 
            graph[i][j] = graph[j][i] = dist(eng) % 2; //1/2的概率连边
        
    

    //打印图
    std::cout << "Graph:" << std::endl;
    for (const auto &row : graph) 
        for (int x : row) 
            std::cout << x << " ";
        
        std::cout << std::endl;
    

    //生成随机树
    std::vector<int> visited(N, 0);
    std::vector<int> tree;
    tree.push_back(0);
    visited[0] = 1;
    while (tree.size() < N) 
        std::vector<int> candidates;
        for (int i : tree) 
            for (int j = 0; j < N; j++) 
                if (graph[i][j] && !visited[j]) 
                    candidates.push_back(j);
                
            
        
        if (candidates.empty()) 
            std::cerr << "Graph is not connected, cannot generate a tree." << std::endl;
            return 1;
        
        std::shuffle(candidates.begin(), candidates.end(), eng); //打乱候选节点顺序
        int new_node = candidates.front();
        tree.push_back(new_node);
        visited[new_node] = 1;
    

    //打印生成的随机树
    std::cout << "Tree: ";
    for (int x : tree) 
        std::cout << x << " ";
    
    std::cout << std::endl;

    return 0;

这个程序使用了C++的STL库中的std::mt19937_64作为随机数生成器，以及std::uniform_int_distribution作为生成随机整数的分布，生成了一个大小为N的随机图和一颗以0为根节点的随机树。程序输出的结果如下：

Graph:
0 0 1 1 0 1 0 0 1 0 
0 0 1 0 0 1 1 0 1 0 
1 1 0 0 1 0 1 0 1 0 
1 0 0 0 0 0 1 1 0 0 
0 0 1 0 0 1 0 0 0 0 
1 1 0 0 1 0 0 0 0 1 
0 1 1 1 0 0 0 0 0 0 
0 0 0 1 0 0 0 0 0 0 
1 1 1 0 0 0 0 0 0 1 
0 0 0 0 0 1 0 0 1 0 
Tree: 0 2 1 6 3 8 5 4 9 7

结语 ：总之，随机数使用的方法很多，还请根据读者由实际情况自己思考体会。

软件测试-黑盒测试 随机测试技巧

黑盒测试（一）-随机测试

一、随机测试一些小技巧

  • 平方取中法
  • 随机数生成服务: https://www.random.org/    推荐一个随机数生成网站
  • 模糊测试技术: 安全性领域，非法输入，让软件发生崩溃

二、经验总结

  • 导致程序出错的用例，可能存在聚集特性
  • 导致程序出错的用例，存在矩形状分布，条状分布，点状分布

技术分享

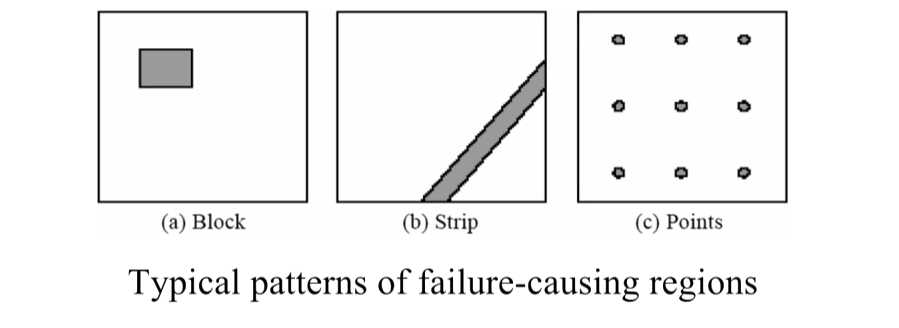
  • 随机测试中，到尽可能远的地方去测试

技术分享

二、自适应随机测试技术

  • FSCS-ART algorithm （自适应随机测试技术）

技术分享

三、Anti-Random Testing

一、算法思想：

  • 随机选择一条测试用例
  • 第二条测试用例，需要计算测试用例与此前已有测试用例的海明距离之和
  • 找到与此前已经测试用例的海明距离之和最大
  • Repeat...

二、实例

test1 = 00000000

test2 = 11111111   //THM(test2) = 8

test3 = 00001111   //THM(test3) = 8

test4 = 11110000   //THM(test4) = 16

 

以上是关于随机造数据的技巧总结的主要内容，如果未能解决你的问题，请参考以下文章

用Yapi 造数据的时候一些简单使用技巧

技巧总结-2018-06

MySQL索引类型总结和使用技巧

软件测试-黑盒测试 随机测试技巧

熬夜总结了53个Python干货技巧，建议收藏

熬夜总结了53个Python干货技巧，建议收藏