[动态规划-背包问题入门] 原理，运用，实战

Posted 2023-05-03 Akira的博客

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[动态规划-背包问题入门] 原理，运用，实战相关的知识，希望对你有一定的参考价值。

动态规划背包问题

背包问题 -- 动态规划经典类型

动态规划是将问题细分为有限个小问题并通过递推或递归来求得最终值。具象化来说，就是对某一问题的答案，我们转化为dp[n]，而对于0 <= i < n，dp[i][j] 的值会根据前后上下的相关值来变化（i.e. dp[i-1][j]或dp[i][j-1]）。注意这时算法强调的不是【容量】，而是【上下文】，即当遍历到第i个对象时，根据对象i有无被包含的情况来判断是否更新dp[i][j]。

而背包问题则是强调了【容量】，即给定一个固定大小的背包，算法需要在有限的空间找出最优解。这就和上下文失去了联系，对于任意对象i，假设其重量为weights[i]，目前最大重量为j，则dp[i][j] = dp[i-1][j-weights[i]] + weights[i]，dp[i][j]就是在最大重量为j的时候带上对象i的最大重量，注意这个前提是j - weights[i]>=0。

相似地，二维数组中dp[i][j]只与dp[i-1]一行相关，因此可以进行空间优化，将dp数组优化为一维数组。这也是很多动态规划问题中可选的优化方式。

运用

下面这段伪代码大概展示了如何用代码解决背包问题，当然根据具体的情况，会有很大的调整，比如内外循环的选择，dp[j]取值的选择等等。

int backpack(vector<int>& weights, int maxWeight):
  create dp(weights.size() + 1); // 包括一个dp[0]作为边界
  for j = 1 -> n 
    for each item:
	if weights[item] <= j:
	  // 背包需要空出存放item的位置
	  dp[j] = weights[item] + dp[j-weights[item]]
  return dp[n];

实战

完美平方数 https://leetcode.cn/problems/perfect-squares/?envType=study-plan-v2&id=dynamic-programming
零钱兑换II https://leetcode.cn/problems/coin-change-ii/?envType=study-plan-v2&id=dynamic-programming
将遍历物品放在外循环，以避免相同元素不同排列的情况
组合总和IV https://leetcode.cn/problems/combination-sum-iv/?envType=study-plan-v2&id=dynamic-programming
注意C++的int大小，如果超出int范围的则需要另外处理
一和零 https://leetcode.cn/problems/ones-and-zeroes/
该题中有两个容量，所以一般来说需要一个三位数组以包括这两个容量以及物品，也可以优化成一个二维数组

小白学习动态规划：0-1背包

小白学习动态规划：0-1背包（经典例题）

前言

背包问题只是动态规划问题下的一个分类，求解0-1背包问题的思路本质上与求解动态规划的一般思路是一致的，我们经常遇到新的题目做不出来，并不是因为没有掌握动态规划的思想，而有可能是因为没有遇到这类具有显著特征的题目，无法将一般动态规划的解题思路应用在实战中。

动态规划的原理：

① 最优子结构性质：问题的最优解可以转化为求子问题的最优解，也就是说问题的最优解可以从子问题的最优解中得出。

② 子问题重叠性质：问题的解由子问题的解组成，所以先构造子问题的解，才能求出最终问题的解。而求问题的解时，由于已经记录子问题的解，所以不必重新求子问题的解，只需取出来使用即可。

经典例题

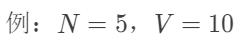
小白学习动态规划：0-1背包

物品	A	B	C	D	E
Wealth	3	4	5	6	7
Cost	1	2	5	6	8

这是最基础的0-1背包问题

先看下图，是在求出问题的解后整个动态规划表呈现的结果。下面就来看看这张表是如何一步步填上去并求出最终问题解的。

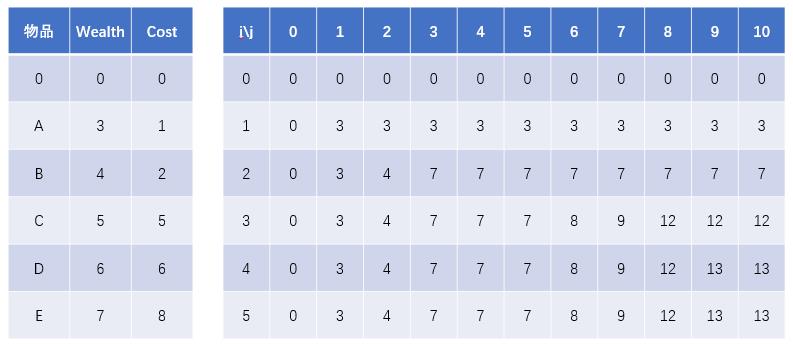
解题思路

① 确定子问题

求容量为V的背包装入物品的价值总和最大，则考虑第i件物品是否放入背包，使得背包的价值保持最大。

② 确定状态及数组

用一个二维数组F[i][j]表示前i件物品放入容量为j的背包中可以获得的最大价值（注意此处的容量是背包的总容量，而不是背包的剩余容量）

③ 确定边界值

F[0][0..V] = 0：表示不管第0件物品放入任意容量的背包中其最大价值都是0，因为不存在第0件物品。

F[0..N][0] = 0：表示任意物品放入容量为0的背包中其最大价值都是0，因为容量为0的背包装不下任何物品。

④ 确定状态转移方程

Ⅰ：若第i件物品无法放入容量为j的背包中

Ⅱ：若第i件物品可以放入容量为j的背包中，则分两种情况：

例：

第Ⅰ种情况：

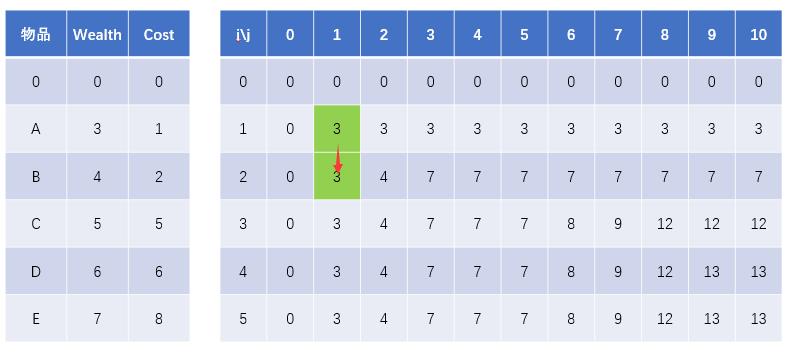
当[i，j] = [2，1]时，物品B的耗费空间Cost=2，而背包的体积 j=1，很明显物品B无法放入背包中，所以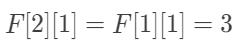
小白学习动态规划：0-1背包
第Ⅱ种情况：

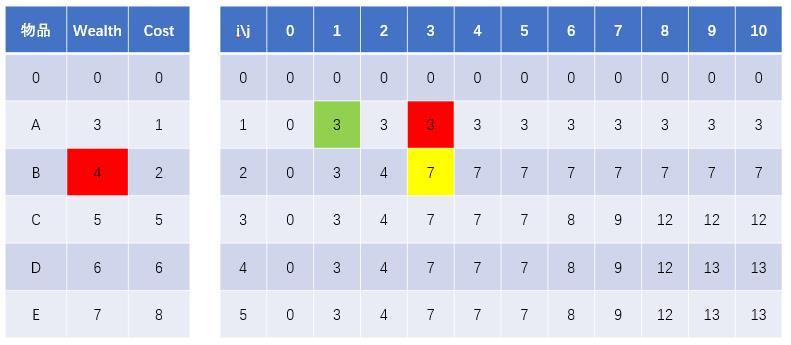
当[i，j] = [2，3]时，物品B的耗费空间Cost = 2，而背包的体积 j=3，物品B可以放入背包中，所以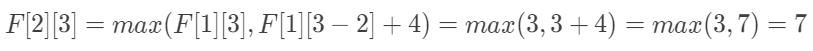
小白学习动态规划：0-1背包

作者在理解Ⅱ时有一个困惑：为什么第i件物品可以放入容量为j的背包中还需要比较不放入的情况？

这是本文的重点

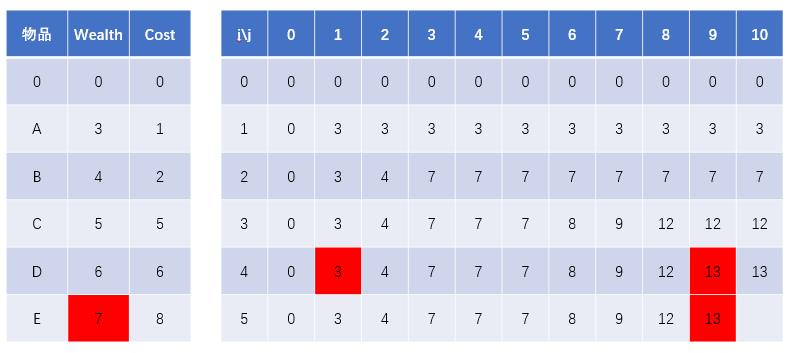
所以并不是说物品E可以放入就马上放入，因为每放入一件物品都要腾出相应的空间
小白学习动态规划：0-1背包

而腾出的空间可以放入其它物品，而有可能放入其它的物品价值总和大于物品E的价值。

⑤ 代码实现

 1public class Solution{
 2    public int dp(int[] wealth, int[] cost, int V, int N){
 3        //特殊状态处理
 4        if(wealth.length != cost.length){return -1;}
 5        if(wealth.length == 0){return 0;}
 6        if(wealth.length == 1){
 7            if(cost[0] > V){
 8                return 0;
 9            }else{
10                return wealth[0];
11            }
12        }
13        int[][] F = new int[N + 1][V+1];
14        //边界值处理
15        for(int i = 1; i < N + 1; i++){
16            for(int j = 1; j < V + 1; j++){
17                //先假设不能放入容量为j的背包
18                F[i][j] = F[i-1][j];
19                //判断能不能放入背包
20                if(j > cost[i-1]){
21                    F[i][j] = Math.max(F[i-1][j], F[i-1][j-cost[i-1]] + wealth[i-1]);
22                }
23            }
24        }
25        return F[N][V];
26    }
27}