python 二叉树的遍历及常见操作

Posted 2020-12-10 r1-12king的学习之路

一、基础

1、 定义节点类

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

 

2、给定一张图

 

 

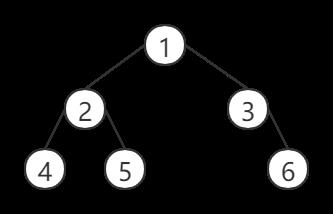
二、基础遍历

1、前序遍历、中序遍历、后续遍历的递归解法

# 前序遍历 [1,2,4,5,3,6]
def preTraverse(root):
    if root == None:
        return
    print(root.value)
    preTraverse(root.left)
    preTraverse(root.right)

# 中序遍历 [4 2 5 1 3 6]
def preTraverse(root):
    if root == None:
        return
    preTraverse(root.left)
    print(root.value)
    preTraverse(root.right)

# 后序遍历 [4 5 2 3 6 1]
def preTraverse(root):
    if root == None:
        return
    preTraverse(root.left)
    preTraverse(root.right)
    print(root.value)

 

2、前序遍历、中序遍历、后续遍历的非递归解法

# 前序遍历
def preTraverse_nonRec(root):
    if not root:
        return None
    stack = []
    res = []
    while root or len(stack):
        while root:
            stack.append(root)
            res.append(root.val)
            root = root.left
        if len(stack):
            root = stack[-1]
            stack.pop()
            root = root.right
    return res

# 中序遍历
def midTraverse_nonRec(root):
    if not root:
        return None
    stack = []
    res = []
    while root or stack:
        while root:
            stack.append(root)
            root = root.left
        root = stack.pop()
        res.append(root.val)
        root = root.right
    return res

# 后序遍历
def afterTraverse_nonRec(root):
    if not root:
        return None
    stack = []
    res = []
    pLast = None
    while root:
        stack.append(root)
        root = root.left
        # 开始出栈
    while len(stack):
        root = stack[-1]
        stack.pop()
        # 若无右子树或者右子树被访问，则访问该节点
        if not root.right or root.right == pLast:
            res.append(root.val)
            pLast = root
        else:
            # 节点再次入栈
            stack.append(root)
            root = root.right
            while root:
                stack.append(root)
                root = root.left
    return res

 

 

3、广度优先遍历（BFS）和深度优先遍历（DFS)

3.1 广度优先遍历（BFS）

　　广度优先遍历（BFS）又叫层次遍历。用队列实现，依次将根，左子树，右子树存入队列，按照队列的先进先出规则来实现层次遍历.

# 定义广度优先遍历(层次遍历)方法
# [1 2 3 4 5 6]
def BFS(root):
    # 仍然是用队列的方式实现遍历，末端按遍历顺序逐个添加节点，首端逐个弹出先读到的节点
    if root:
        res = []
        queue = [root]
        while queue:
            currentNode = queue.pop(0)
            res.append(currentNode.val)
            if currentNode.left:
                queue.append(currentNode.left)
            if currentNode.right:
                queue.append(currentNode.right)
    return res

 

3.2 深度优先遍历（DFS）

　　用栈实现，先将根入栈，再将根出栈，并将根的右子树，左子树存入栈，按照栈的先进后出规则来实现深度优先遍历。

# 深度优先
# [1,2,4,5,3,6]
def DFS(root):
    if root:
        res = []
        stack = [root]
        while stack:
            currentNode = stack.pop()
            res.append(currentNode.val)
            if currentNode.right:
                stack.append(currentNode.right)
            if currentNode.left:
                stack.append(currentNode.left)
    return res

 

 

三、常见操作

1、求节点个数

def count_BinTNodes(t):
    if t is None:
        return 0
    else:
        return 1 + count_BinTNodes(t.left) \\
               + count_BinTNodes(t.right)

 

2、求节点的值得总和

def sum_BinTNodes(t):
    if t is None:
        return 0
    else:
        return t.value + sum_BinTNodes(t.left) \\
               + sum_BinTNodes(t.right)

3、二叉树的最大深度

　　基本思路就是递归，当前树的最大深度等于（1+max(左子树最大深度，右子树最大深度)）。

def maxDepth(root):
    if not root:
        return 0
    return 1+max(maxDepth(root.left),maxDepth(root.right))

 

4、 二叉树的最小深度

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。可以通过递归求左右节点的最小深度的较小值，也可以层序遍历找到第一个叶子节点所在的层数。

# 递归方法：
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        if not root.left and not root.right:
            return 1 
        if not root.right:
            return 1+self.minDepth(root.left)
        if not root.left:
            return 1+self.minDepth(root.right)
        return 1+min(self.minDepth(root.left),self.minDepth(root.right))


# 迭代方法：
class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root: return 0
        ans,count = [root],1
        while ans:
            n = len(ans)
            for i in range(n):
                r = ans.pop(0)
                if r:
                    if not r.left and not r.right:
                        return count
                    ans.append(r.left if r.left else [])
                    ans.append(r.right if r.right else [])
            count+=1 

 

5、二叉树的最大宽度

# 求树的最大宽度
def treeWidth(root):
    curWidth = 1
    maxWidth = 0
    myQueue = []
    myQueue.append(root)
    while myQueue:
        n = curWidth
        for i in range(n):
            node = myQueue.pop(0)
            curWidth -= 1
            if node.left != None:
                myQueue.append(node.left)
                curWidth += 1
            if node.right != None:
                myQueue.append(node.right)
                curWidth += 1
        if curWidth > maxWidth:
            maxWidth = curWidth
    return maxWidth

 

6、求二叉树的叶子节点

　　可以使用树的任意一种深度优先遍历方法，在这里用的是先序。

def get_leaves(root):
    res = []
    stack = []
    while root or stack:
        while root:
            stack.append(root)
            if not root.left and not root.right:
                res.append(root.val)
            root = root.left
        if stack:
            root = stack.pop()
            root = root.right
    return res