代码更新版:
# 商品列表。w:重量;v:价值
tr = [{\'w\':1,\'v\':1500},{\'w\':4,\'v\':3000},{\'w\':3,\'v\':2000}]
max_w = 4 # 背包容量
# 生成一个二维数组dp[i][j],i代表几个物品,j代表容量。dp[i][j]代表在背包容量为j,偷盗物品为i个时的最大价值。
dp = [[0]*(max_w+1) for i in tr]
for j in range(1,max_w+1): # 先随便偷一个物品,放到各种规格的背包容器内,作为后来物品的参照。
if tr[0][\'w\'] <= j: # 当物品能放进当前规格,当前规格的价值就是物品的价值喽
dp[0][j] = tr[0][\'v\']
for i in range(1,len(tr)): # 对之后的物品尝试
for j in range(1,max_w+1):
if tr[i][\'w\'] > j: # 如果放不下当前物品,背包能放的价值,就是之前存放组合规格下的价值。
dp[i][j] = dp[i-1][j]
else: # 能放下,当前规格的价值=max(当前物品的价值+剩余空间的价值,之前物品组合同等规格的价值)
dp[i][j] = max( dp[i-1][j],tr[i][\'v\']+dp[i-1][j-tr[i][\'w\']] )
print(dp)
示例:
# g1{w:1,v:3},g2{w:3,v:5},g3{w:4,v:7}
# w1 w2 w3 w4 背包的四种规格:1,2,3,4
# g1 3 3 3 3 此行只有g1物品可供选择,所以每个背包最大价值就是g1的3
# g2 3 3 5 8 此处有g1-g2可供选择,w1-w2时无法放入g2,所以还是g1的3;w3时可以放入g2,g2:5>g1:3 选5;w4时能放入5,但是剩余空间1,而剩余的1,又能放入价值3的g1,价值5+3=8 > g1的3,故8:g1+g2
# g3 3 3 5 8 有g1-g3可供选择,w4时能放入并刚好占满空间,所以如果放g3,最大价值为7,但是7<8,故不拿g3,选择之前的8的组合
代码实现:
goods = {\'吉他\':{\'wei\':1,\'val\':1500} ,\'音响\':{\'wei\':4,\'val\':3000},\'电脑\':{\'wei\':3,\'val\':2000}}
def bag(goods,con):
# con: 背包容量, goods,商品
# 获取最轻的物品重量
min_con = con
for good in goods.values():
if good[\'wei\'] <= min_con:
min_con = good[\'wei\']
# 以最轻物品的重量为单位,生成各种规格的背包
b = {} # 各种大小的背包的集合
weigh_list = [] # 背包规格
weigh = min_con
while weigh < con:
b[weigh] = []
weigh_list.append(weigh)
weigh += min_con
if weigh >= con:
b[con] = []
weigh_list.append(con)
# print(b,weigh_list) # b = {1: [], 2: [], 3: [], 4: [], 5: []} ; weigh_list = [1, 2, 3, 4, 5]
used = []
for name in goods: # 遍历物品
row = len(used)
for weigh in weigh_list: # 遍历背包
print(b)
if goods[name][\'wei\'] <= weigh: # 如果当前物品能装进背包
if row == 0: # 如果当前物品是第一个装进背包的,能存放的价值就是当前物品的价值
print(\'物品:\',name,\'重量\',goods[name][\'wei\'],\'背包空间\',weigh,\'放进去了\')
b[weigh].append(goods[name][\'val\'])
else: # 如果之前已经有物品尝试放进背包,就对比一下物品价格,要最值钱的
# 算出盛放当前物品后是否有剩余空间,以及剩余空间能存放的价值
remain_weigh = weigh - goods[name][\'wei\']
remain_val = 0
if remain_weigh > 0: # 放了当前物品,还有剩余空间
for num,w in enumerate(weigh_list):
if w > remain_weigh: # 找到一个刚好能放下的空间
remain_val = b[weigh_list[num-1]][row-1] # 找出这个空间能放的价值
break
print(\'物品:\',name,\'重量\',goods[name][\'wei\'],\'背包空间\',weigh,\'放进去了\',\'剩余空间和价值\',remain_weigh,remain_val)
# 如果整个空间的价值超过之前 同重量情况下能存放的最大价值,就更新一下这种规格背包的最大价值
if goods[name][\'val\']+remain_val > b[weigh][row-1]:
b[weigh].append(goods[name][\'val\']+remain_val)
else: # 否则这个空间的最大价值还是之前的价值
b[weigh].append(b[weigh][row-1])
else: # 背包装不下当前物品,沿用上一个物品的价值
print(\'物品:\',name,\'重量\',goods[name][\'wei\'],\'背包空间\',weigh,\'放不下\')
b[weigh].append(b[weigh][row-1])
used.append(name) # 每将一个物品尝试完所有背包规格,就把这个物品放到尝试过的列表中
for value in b.values():
print(value)
bag(goods,4) # 4是背包大小
运行结果:
{1: [], 2: [], 3: [], 4: []}
物品: 吉他 重量 1 背包空间 1 放进去了
{1: [1500], 2: [], 3: [], 4: []}
物品: 吉他 重量 1 背包空间 2 放进去了
{1: [1500], 2: [1500], 3: [], 4: []}
物品: 吉他 重量 1 背包空间 3 放进去了
{1: [1500], 2: [1500], 3: [1500], 4: []}
物品: 吉他 重量 1 背包空间 4 放进去了
{1: [1500], 2: [1500], 3: [1500], 4: [1500]}
物品: 音响 重量 4 背包空间 1 放不下
{1: [1500, 1500], 2: [1500], 3: [1500], 4: [1500]}
物品: 音响 重量 4 背包空间 2 放不下
{1: [1500, 1500], 2: [1500, 1500], 3: [1500], 4: [1500]}
物品: 音响 重量 4 背包空间 3 放不下
{1: [1500, 1500], 2: [1500, 1500], 3: [1500, 1500], 4: [1500]}
物品: 音响 重量 4 背包空间 4 放进去了 剩余空间和价值 0 0
{1: [1500, 1500], 2: [1500, 1500], 3: [1500, 1500], 4: [1500, 3000]}
物品: 电脑 重量 3 背包空间 1 放不下
{1: [1500, 1500, 1500], 2: [1500, 1500], 3: [1500, 1500], 4: [1500, 3000]}
物品: 电脑 重量 3 背包空间 2 放不下
{1: [1500, 1500, 1500], 2: [1500, 1500, 1500], 3: [1500, 1500], 4: [1500, 3000]}
物品: 电脑 重量 3 背包空间 3 放进去了 剩余空间和价值 0 0
{1: [1500, 1500, 1500], 2: [1500, 1500, 1500], 3: [1500, 1500, 2000], 4: [1500, 3000]}
物品: 电脑 重量 3 背包空间 4 放进去了 剩余空间和价值 1 1500
[1500, 1500, 1500]
[1500, 1500, 1500]
[1500, 1500, 2000]
[1500, 3000, 3500]
分析:摘取自《算法图解》
假设你是个小偷,背着一个可装4磅东西的背包。你可盗窃的商品有如下3件。为了让盗窃的商品价值最高,你该选择哪些商品?

每个动态规划算法都从一个网格开始,背包问题的网格如下。
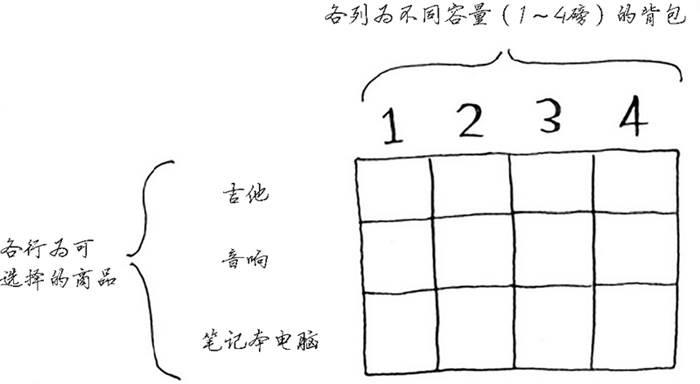
- 吉他行
后面将列出计算这个网格中单元格值的公式。我们先来一步一步做。首先来看第一行。
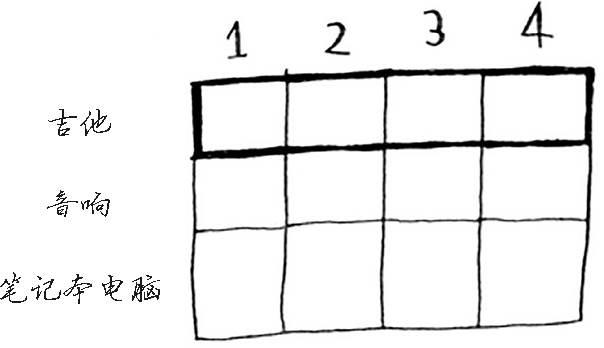
这是吉他行,意味着你将尝试将吉他装入背包。在每个单元格,都需要做一个简单的决定:偷不偷吉他?别忘了,你要找出一个价值最高的商品集合。
第一个单元格表示背包的容量为1磅。吉他的重量也是1磅,这意味着它能装入背包!因此这个单元格包含吉他,价值为1500美元。
下面来开始填充网格。
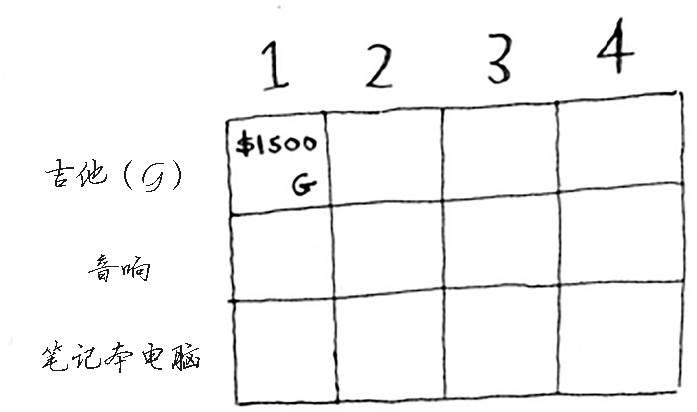
与这个单元格一样,每个单元格都将包含当前可装入背包的所有商品。
来看下一个单元格。这个单元格表示背包的容量为2磅,完全能够装下吉他!
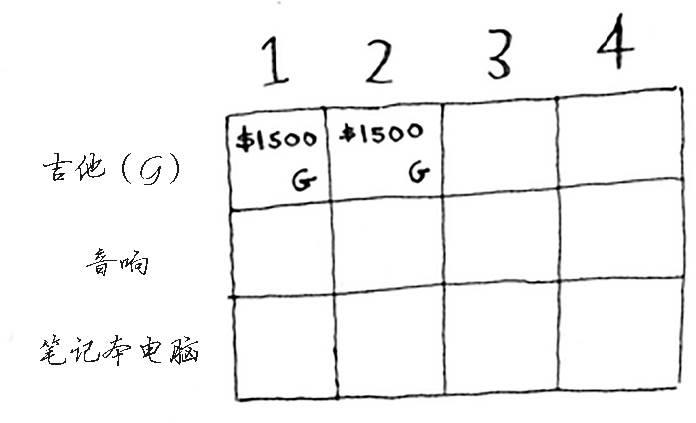
这行的其他单元格也一样。别忘了,这是第一行,只有吉他可供你选择。换言之,你假装现在还没法盗窃其他两件商品。
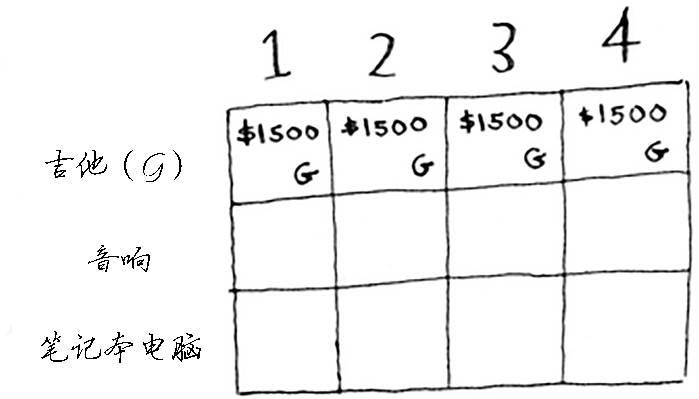
此时你很可能心存疑惑:原来的问题说的是4磅的背包,我们为何要考虑容量为1磅、2磅等的背包呢?前面说过,动态规划从小问题着手,逐步解决大问题。这里解决的子问题将帮助你解决大问题。请接着往下读,稍后你就会明白的。
此时网格应类似于下面这样。
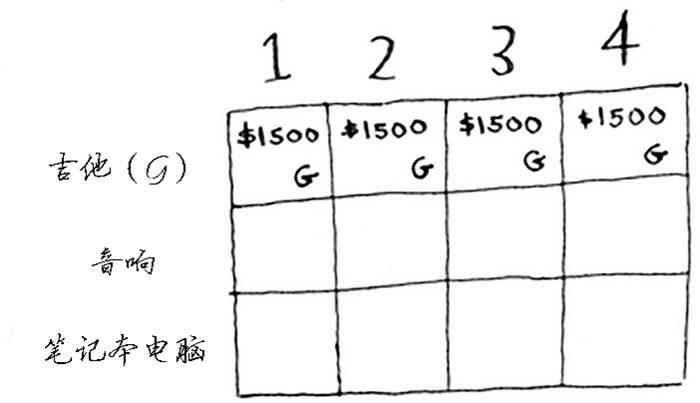
别忘了,你要做的是让背包中商品的价值最大。这行表示的是当前的最大价值 。它指出,如果你有一个容量4磅的背包,可在其中装入的商品的最大价值为1500美元。
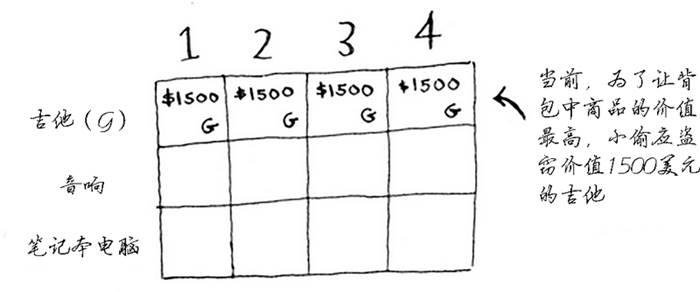
你知道这不是最终的解。随着算法往下执行,你将逐步修改最大价值。
- 音响行
我们来填充下一行——音响行。你现在出于第二行,可偷的商品有吉他和音响。在每一行,可偷的商品都为当前行的商品以及之前各行的商品。因此,当前你还不能偷笔记本电脑,而只能偷音响和吉他。我们先来看第一个单元格,它表示容量为1磅的背包。在此之前,可装入1磅背包的商品的最大价值为1500美元。
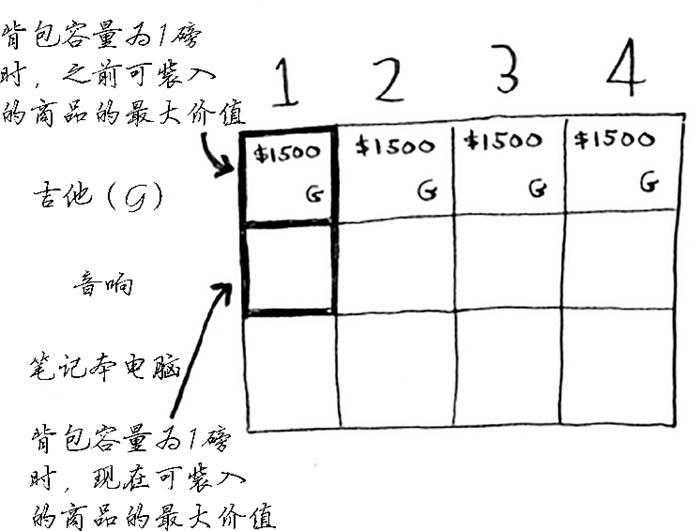
该不该偷音响呢?
背包的容量为1磅,能装下音响吗?音响太重了,装不下!由于容量1磅的背包装不下音响,因此最大价值依然是1500美元。
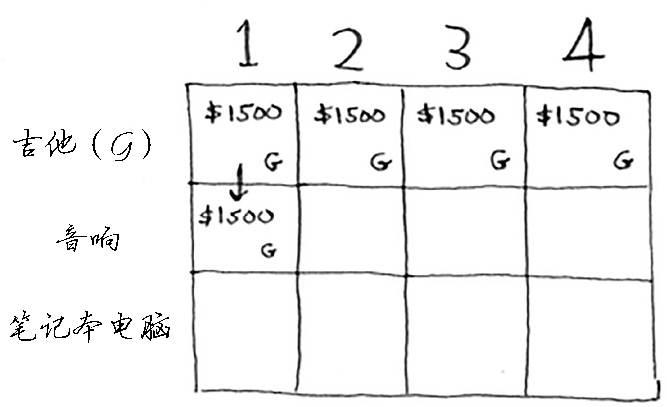
接下来的两个单元格的情况与此相同。在这些单元格中,背包的容量分别为2磅和3磅,而以前的最大价值为1500美元。
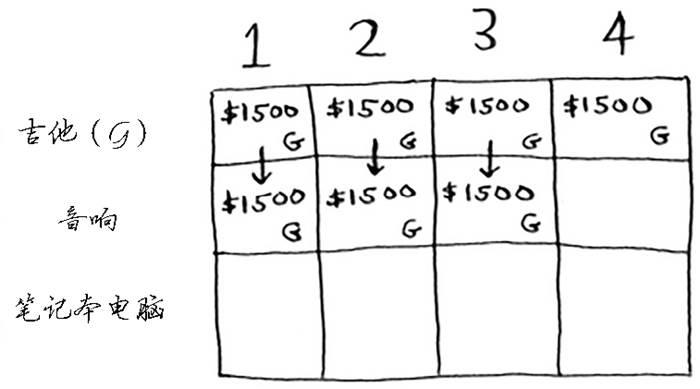
由于这些背包装不下音响,因此最大价值保持不变。
背包容量为4磅呢?终于能够装下音响了!原来的最大价值为1500美元,但如果在背包中装入音响而不是吉他,价值将为3000美元!因此还是偷音响吧。
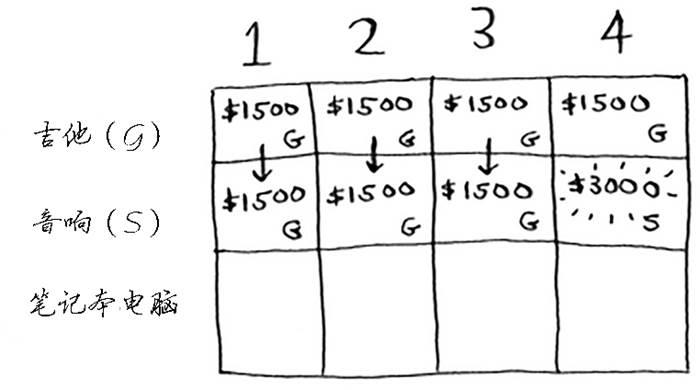
你更新了最大价值!如果背包的容量为4磅,就能装入价值至少3000美元的商品。在这个网格中,你逐步地更新最大价值。
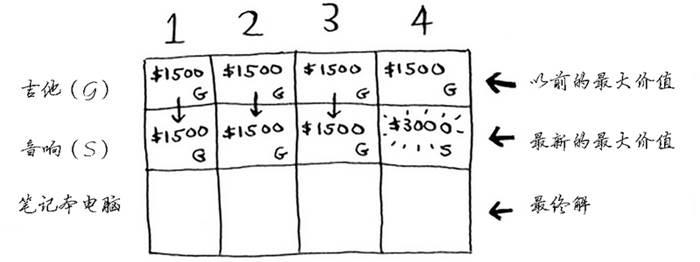
- 笔记本电脑行
下面以同样的方式处理笔记本电脑。笔记本电脑重3磅,没法将其装入容量为1磅或2磅的背包,因此前两个单元格的最大价值还是1500美元。
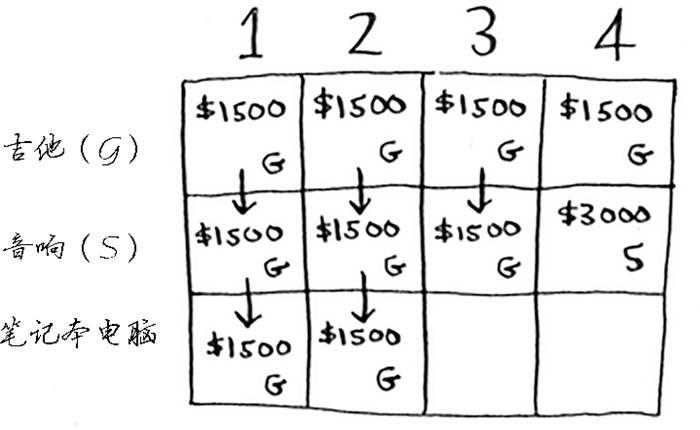
对于容量为3磅的背包,原来的最大价值为1500美元,但现在你可选择盗窃价值2000美元的笔记本电脑而不是吉他,这样新的最大价值将为2000美元!
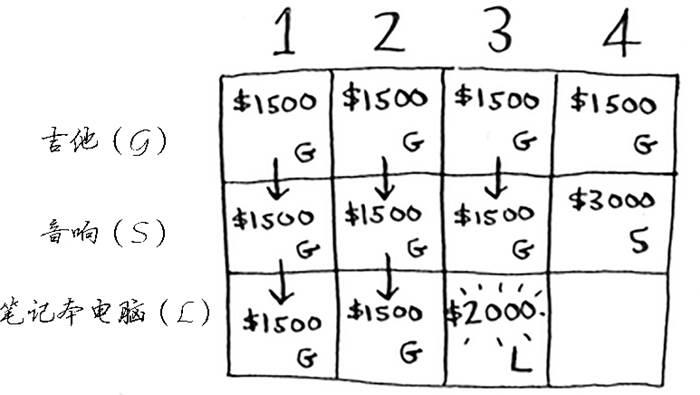
对于容量为4磅的背包,情况很有趣。这是非常重要的部分。当前的最大价值为3000美元,你可不偷音响,而偷笔记本电脑,但它只值2000美元。

价值没有原来高。但等一等,笔记本电脑的重量只有3磅,背包还有1磅的容量没用!

在1磅的容量中,可装入的商品的最大价值是多少呢?你之前计算过。
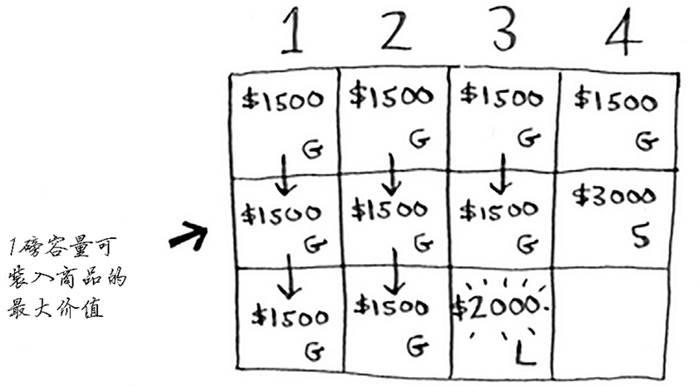
根据之前计算的最大价值可知,在1磅的容量中可装入吉他,价值1500美元。因此,你需要做如下比较。

你可能始终心存疑惑:为何计算小背包可装入的商品的最大价值呢?但愿你现在明白了其中的原因!余下了空间时,你可根据这些子问题的答案来确定余下的空间可装入哪些商品。笔记本电脑和吉他的总价值为3500美元,因此偷它们是更好的选择。
最终的网格类似于下面这样。
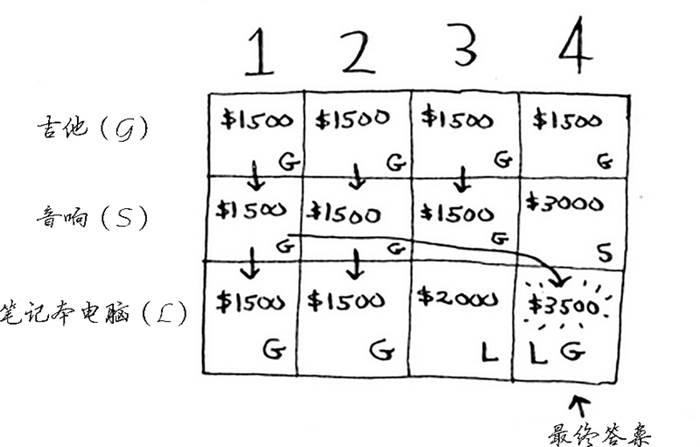
答案如下:将吉他和笔记本电脑装入背包时价值最高,为3500美元。
你可能认为,计算最后一个单元格的价值时,我使用了不同的公式。那是因为填充之前的单元格时,我故意避开了一些复杂的因素。其实,计算每个单元格的价值时,使用的公式都相同。这个公式如下。

你可以使用这个公式来计算每个单元格的价值,最终的网格将与前一个网格相同。现在你明白了为何要求解子问题吧?你可以合并两个子问题的解来得到更大问题的解。