给出一个立方体的三维坐标如何在二维平面上画出,问题一般化就是如何把一个三维坐标转换成二维坐标？

Posted 2023-05-02

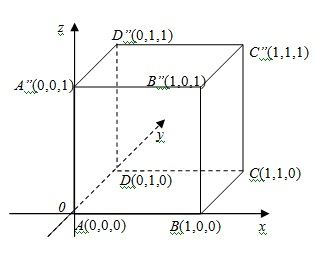
已知：正方体各顶点坐标A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),A"(0,0,1),B"(1,0,1),C"(1,1,1),D"(0,1,1)

求作：在二维平面上画出正方体ABCD-A“B”C“D”

作法：1，在二维平面上建立三维坐标系xyz；

      2，在xyz坐标系中用斜二测画法作出各点；

      3，依次连结各点，即为所求作；（如图）

讨论：x轴向、z轴向的点按距离作出；y轴向的点按斜二测画法，向右（或左）倾斜45°，距离缩小为原的一半。也即是坐标轴上的单位长度为原一半。

参考技术A 说的有点模糊，感觉是不是有立方体的各个点的坐标，然后在直角坐标系上画出来。那样你可以在三维坐标轴上画出图形，然后像做三视图一样的做投影 参考技术B 个人觉得先通过三维坐标绘制出相应的点位，再在空间坐标系中用连接各点，做出三维模型。这样就可以投影平面视图了。

利用暴力法解决“三维形体投影面积”问题

二十四、三维形体投影面积

24.1、题设要求

  在 n x n 的网格 grid 中，我们放置了一些与 x，y，z 三轴对齐的 1 x 1 x 1 立方体。

  每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。

  现在，我们查看这些立方体在 xy 、yz 和 zx 平面上的投影。

  投影 就像影子，将 三维 形体映射到一个 二维 平面上。从顶部、前面和侧面看立方体时，我们会看到“影子”。

  返回 所有三个投影的总面积 。

示例 1：

输入：[[1,2],[3,4]]
输出：17
解释：这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

示例 2:

输入：grid = [[2]]
输出：5

示例 3：

输入：[[1,0],[0,2]]
输出：8

提示：

n == grid.length == grid[i].length
1 <= n <= 50
0 <= grid[i][j] <= 50

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/projection-area-of-3d-shapes

24.2、解题思路

  根据题意进行模拟即可，使用三个变量分别统计三视图的阴影面积：

  xyArea：统计俯视图的面积，共有 n * n 个位置需要被统计，当任意格子 g[i] [j]>0，阴影面积加一；
  yzArea：统计左视图的面积，共有 n 行需要被统计，每一行对 ans2 的贡献为该行的最大高度；
  zxArea：统计主视图的面积，共有 n 列需要被统计，每一列对 ans3 的贡献为该列的最大高度。

24.3、算法

class Solution 
    public int projectionArea(int[][] grid) 
        int n = grid.length;
        int xyArea = 0, yzArea = 0, zxArea = 0;
        for (int i = 0; i < n; i++) 
            int yzHeight = 0, zxHeight = 0;
            for (int j = 0; j < n; j++) 
                xyArea += grid[i][j] > 0 ? 1 : 0;
                yzHeight = Math.max(yzHeight, grid[j][i]);
                zxHeight = Math.max(zxHeight, grid[i][j]);
            
            yzArea += yzHeight;
            zxArea += zxHeight;
        
        return xyArea + yzArea + zxArea;