Treap 学习笔记
Posted qwq-qaq-tat
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Treap 学习笔记相关的知识,希望对你有一定的参考价值。
一、Treap
Treap 是一种通过旋转操作维护性质的二叉搜索树。
定义详见
要维护的东西还是一样,对于每个节点,要维护它的左右儿子,子树大小,还有权值和随机的优先级(这样才能保证树的高度是 \\(O(\\log n)\\) 级别的)。
注意:旋转、分裂、伸展什么的都是手段,维持平衡树的 2 个性质才是目的。
对于全局,要维护树根的编号和当前有多少个节点。
二、实现
1. 旋转
由于插入、删除操作需要维护二叉搜索树的性质,所以我们需要一个操作来调整 Treap。它的核心操作就是旋转。
旋转的目标是在整棵树的中序遍历不变的情况下改变父子关系,让优先级小的节点更浅。而中序遍历递增可以在插入、删除操作中维护。

我们惊喜地看到,全树中序遍历没有变(都是 4 的子树->2->5 的子树->1->3 的子树),并且有且仅有 1、2 父子关系改变了。
然后来讲一下旋转操作具体怎么做。先放代码。
1. 维护操作
维护一个节点的子树大小,就是它自己加上左右子树的大小。
void upd(int x)
t[x].s=t[t[x].l].s+t[t[x].r].s+1;
时间复杂度 \\(O(1)\\)。
2. 右旋
inline void rrot(int &x)
int y=t[x].l;
t[x].l=t[y].r;
t[y].r=x;
upd(x);
upd(y);
x=y;
大概就是这样(绿色的节点表示维护完成):
- 记录 \\(y\\) 为 \\(x\\) 的左子节点。

- 令 \\(x\\) 的左节点变为 \\(y\\) 的右节点。
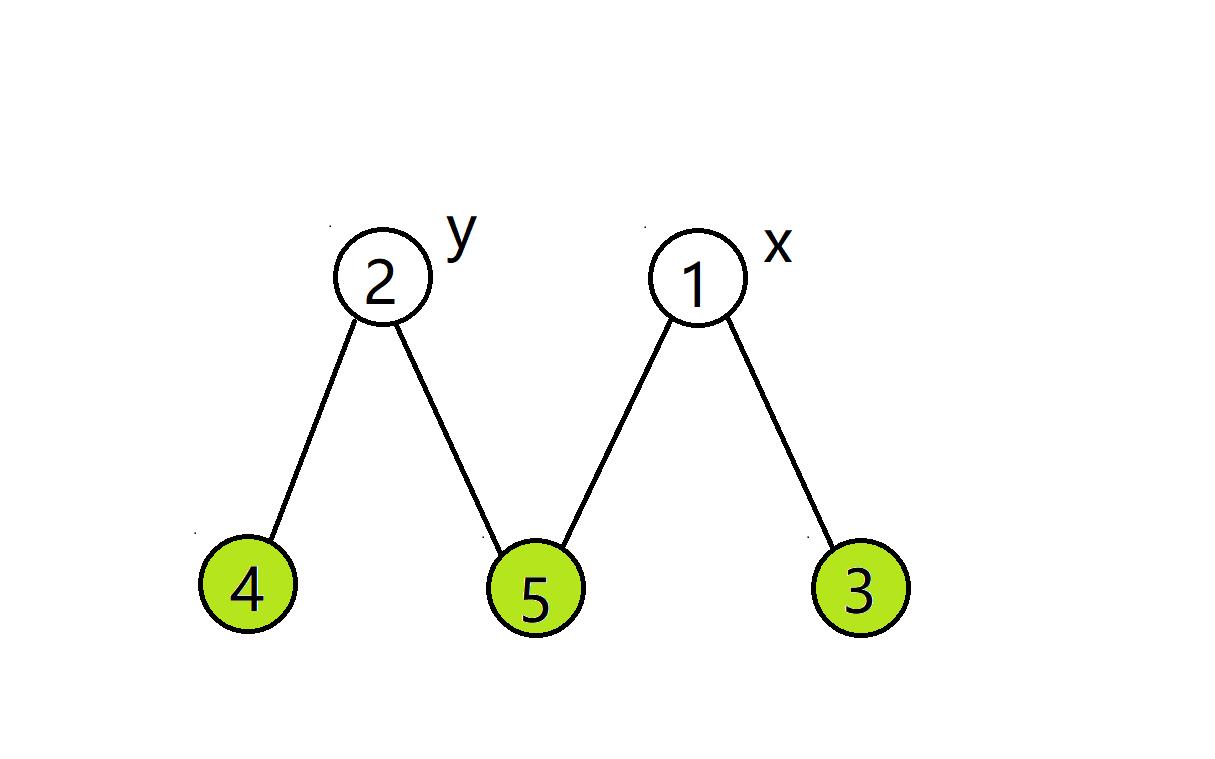
- 令 \\(y\\) 的右节点变为 \\(x\\)。

- 维护 \\(x\\),再维护 \\(y\\)(顺序不能乱)
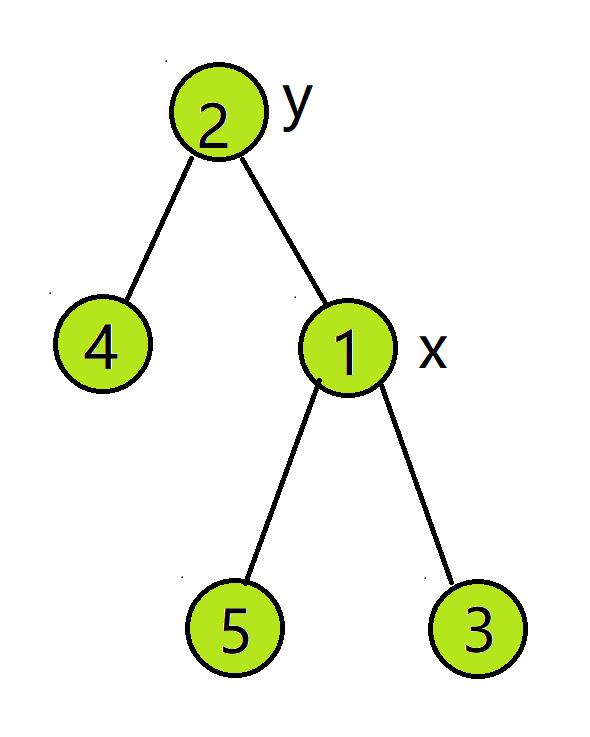
- 令根节点为 \\(y\\)。

时间复杂度 \\(O(1)\\)。
3. 左旋
我们发现,右旋和左旋互为逆运算,而且左右对称,所以我们把右旋的所有左右反过来就行啦。
inline void lrot(int &x)
int y=t[x].r;
t[x].r=t[y].l;
t[y].l=x;
upd(x);
upd(y);
x=y;
时间复杂度 \\(O(1)\\)。
4. 插入
要插入一个数,而且要保证二叉搜索树性质,所以我们递归:
-
判断要插入的数与当前节点的关系。如果小于等于,插入到左子树。否则插入到右子树。
-
如果遇到一个空节点,就新增一个节点并返回。
-
然后回溯时要维护堆性质。那么我们往哪个方向插入了新数字,那个方向的堆性质才会被破坏。所以判断一下那个方向的堆性质有没有被破坏,如果有,进行对应的旋转即可。
inline void ins(int &x,int v)
if(!x)
t[x=++c]=0,0,1,v,rand();
return;
t[x].s++;
if(v<=t[x].v)
ins(t[x].l,v);
if(t[t[x].l].p<t[x].p)rrot(x);
else
ins(t[x].r,v);
if(t[t[x].r].p<t[x].p)lrot(x);
时间复杂度 \\(O(树高)\\),也就是 \\(O(\\log n)\\)。当然实际上跑不满,因为一旦回溯到某一个地方时,发现不用旋转也满足了堆性质,那么这个地方及以上都不用旋转了。
5. 删除
要删除一个数,采用二叉堆的思想,将一个数旋转到叶子节点再删除。由于旋转操作不改变二叉搜索树性质,所以我们要维护堆性质:一个数的优先级小于等于它的儿子。那我们在将一个数向下旋转的时候,肯定是选择一个优先级小的转上来。
inline void del(int &x,int v)
if(t[x].v==v)
if(!t[x].l||!t[x].r)
x=t[x].l+t[x].r;
return;
if(t[t[x].l].p>t[t[x].r].p)
lrot(x);
del(t[x].l,v);
else
rrot(x);
del(t[x].r,v);
else if(t[x].v>v)del(t[x].l,v);
else del(t[x].r,v);
upd(x);
时间复杂度 \\(O(\\log n)\\)。
6. 查询 x 数的排名
照样是分左右子树查询。
注意一定要查询到空节点为止。
inline int vtr(int x,int v)
if(!x)return 1;
if(t[x].v>=v)return vtr(t[x].l,v);
return vtr(t[x].r,v)+t[t[x].l].s+1;
时间复杂度 \\(O(\\log n)\\)。
7. 查询排名为 x 的数
inline int rtv(int x,int v)
if(t[t[x].l].s==v-1)return t[x].v;
if(t[t[x].l].s>=v)return rtv(t[x].l,v);
return rtv(t[x].r,v-1-t[t[x].l].s);
时间复杂度 \\(O(\\log n)\\)。
8. 查询前驱
inline int pre(int x,int v)
if(!x)return -I;
if(t[x].v>=v)return pre(t[x].l,v);
return max(t[x].v,pre(t[x].r,v));
时间复杂度 \\(O(\\log n)\\)。
9. 查询后缀
inline int nxt(int x,int v)
if(!x)return I;
if(t[x].v<=v)return nxt(t[x].r,v);
return min(t[x].v,nxt(t[x].l,v));
时间复杂度 \\(O(\\log n)\\)。
模板fhq-treap
一、什么是(fhq-treap)
(fhq-treap):非旋转(treap),顾名思义,不用像普通(treap)那样繁琐的旋转,只需要通过分裂和合并,就可以实现基本上是所有数据结构能实现的操作,并且短小、精悍,时间复杂度与(splay)齐当,算是一个十分易懂且优秀的算法(并不需要提前学习普通(treap))
接下来,我们就来看看(fhq-treap)是怎么实现的
二、(fhq-treap) 的性质
在这棵平衡树里面,我们保证
左子树节点的权值(在序列中的位置)全部小于根的权值(在序列中的位置),
右子树节点的权值(在序列中的位置)全部大于根的权值(在序列中的位置),
所有分裂和合并操作都满足这个性质
我们还得考虑一个灵魂拷问:为什么(fhq-treap)叫平衡树?
因为它满足平衡性,可以达到期望层数(logn)层,大大减小了时间复杂度
妈妈再也不用担心我的时间复杂度了
三、(fhq-treap) 的两大操作
首先,我们先来明确一下(fhq-treap)里面的基本变量
(ch[2]):两个儿子
(siz):以这个节点为根的子树的大小
(val):这个节点的权值
(rd):这个节点的随机权值,用来保证树的平衡性,在新建节点时由(rand)得到
(rev):这个节点所代表区间的旋转标记,为0或1
(Split):分裂操作
在题目中,有可能以权值排序建树,也可能以序列顺序建树
这里以权值排序建树
我们将一棵树分裂为两部分:权值<=k和权值>k的,我们称这两部分的节点组成的树为(x)和(y)
那么怎么分裂呢?
我们考虑,如果当前节点的权值大于k
那么因为右子树的节点权值明显全部都比k大,所以当前节点以及右子树的节点全部加入(y)树中,接着继续分裂左子树
如果小于等于k同理
因为它的(siz)改变了,所以最后记得(update)当前的树
void split(int now,int k,int &x,int &y)
//将以now为根的子树中权值<=k的节点分裂为x子树,>k的节点分裂为y子树
{
if(!now)x=y=0;
else
{
if(k<t[now].val)//如果当前根的val大于k
{
y=now;//加入y树中
split(t[now].ch[0],k,x,t[y].ch[0]);
//分裂左子树,因为接下来遍历到的节点权值一定小于当前的权值
//所以如果有满足要求的,全部接到y的左子树上,满足性质
up(y);
}
else
{
x=now;//加入x树中
split(t[now].ch[1],k,t[x].ch[1],y);//与上同理
up(x);
}
}
}这是以序列顺序建树的:
void split(int now,int k,int &x,int &y)
{
if(!now)x=y=0;
else
{
if(k<=t[t[now].ch[0]].siz)
{
y=now;
split(t[now].ch[0],k,x,t[y].ch[0]);
up(y);
}
else
{
x=now;
split(t[now].ch[1],k-t[t[now].ch[0]].siz-1,t[x].ch[1],y);
//因为k>左子树的siz,说明k在右子树中
//那么在遍历右子树的时候,所查找的排名要减去左子树的siz和这个节点
up(x);;
}
}
}(Merge):合并操作
我们把子树分裂出来后,肯定要将子树合并回去
所以合并要怎么写呢?
我们在合并时,要考虑到上述的平衡性,所以在合并时要满足平衡性,就要用到随机权值(rd)辅助
如果要将(x),(y)合并,那么当(t[x].rd<t[y[.rd)时,我们就将树(y)接到树(x)上,反之将树(x)接到树(y)上
在这里合并时,因为已经满足了左子树节点的权值小于右子树节点的权值,所以每次合并时
对于接到树(x)上的情况,要接到树(x)的右子树上,对于接到树(y)上的情况,要接到树(y)的左子树上
同样最后也要(update)
int merge(int x,int y)
{
if(!(x&&y))return x+y;
if(t[x].rd<t[y].rd)
{
t[x].ch[1]=merge(t[x].ch[1],y);
up(x);
return x;
}
else
{
t[y].ch[0]=merge(x,t[y].ch[0]);
up(y);
return y;
}
}四、其他操作
(newnode):新建节点
int newnode(int x)
{
t[++nodetot].val=x;
t[nodetot].rd=rand();
t[nodetot].siz=1;
return nodetot;
}(ins):插入操作
我们找出当前节点(x)要插入的位置,将整棵平衡树分裂为(a),(b)两棵子树,分别表示(<=x)和(>x),再依次合并(a,x,b)
以按大小顺序建树:
void ins(int x)
{
int a,b,c;
split(rt,x,a,b);//a树表示<=x,b树表示>x
rt=merge(merge(a,newnode(x)),b);//将x插入其中
}(del):删除操作
对于要删除的节点权值(x),我们先分裂出(a,b)子树,表示(<=x)和(>x),再把(a)分裂出一个(c)子树,使得(a)树(<=x-1),这样,树(c)就是(x)
这时,树(a,b,c)分别表示(<=x-1),(x),(>x)
再直接合并树(c)的左子树和右子树,相当于删除权值为(x)的节点,再依次合并(a,c,b)
void del(int x)
{
int a,b,c;
split(rt,x,a,b);
split(a,x-1,a,c);
c=merge(t[c].ch[0],t[c].ch[1]);
rt=merge(merge(a,c),b);
}(rnk):查询(x)数的排名
先将原树分裂成(a(<=(x-1)),b(>(x-1)))树,括号里面代表节点范围,那么(t[a].siz)代表(<=(x-1))的数的个数,再加上(1)就是(x)的排名
int rnk(int x)
{
int a,b,c;
split(rt,x-1,a,b);
int ans=t[a].siz+1;
rt=merge(a,b);
return ans;
}(kth):查询排名为(k)的数
这是少数几个仅仅用循环就可以解决的问题。
我们可以不断的更新(now),当(now)的左子树的(siz+1=k)时,那么就寻找到了排名为(k)的数,返回答案
在循环中,我们判断当左子树的(siz>=k)时,那么说明排名为(k)的数肯定在左子树中,所以遍历左子树
否则,就更新:(k=k-t[t[now].ch[0]].siz-1),再遍历右子树,不断循环,相当于一个递归的过程
int kth(int now,int k)
{
while((t[t[now].ch[0]].siz+1)!=k)
{
if(t[t[now].ch[0]].siz>=k)now=t[now].ch[0];
else
{
k=k-t[t[now].ch[0]].siz-1;
now=t[now].ch[1];
}
}
return t[now].val;
}(pre):求(x)的前驱(前驱定义为小于(x),且最大的数)
将原树分离为(a(<=x-1),b(>x-1)),那么相当于(a)树中的树都是(<x)的数,并且全部都在(a)树中,按照定义,我们找到(a)树中排名(t[a].siz)的数,就是(a)树中最大的数(右子树的数大于左子树的数),返回答案。
int pre(int x)
{
int a,b,c;
split(rt,x-1,a,b);
int ans=kth(a,t[a].siz);
rt=merge(a,b);
return ans;
}(nxt):求(x)的后继(后继定义为大于(x),且最小的数)
同(pre)操作很像,将原树分离为(a(<=x),b(>x)),那么相当于(b)树中的数都是(>x)的数,按照定义,寻找(b)树中排名第一的数(最小),返回答案。
int nxt(int x)
{
int a,b,c;
split(rt,x,a,b);
int ans=kth(b,1);
rt=merge(a,b);
return ans;
}(turn):翻转区间
(p.s:)例如:原有序序列是(5) (4) (3) (2) (1),翻转区间是([2,4])的话,结果是(5) (2) (3) (4) (1)
这个是按照(siz)来排序建树的,因为题目要求的是翻转区间,并不是按照数大小排序,所以用(siz)排序
在这里,我们将([x,y])区间提取出来为(b)树,在(b)树上打标记(rev) ^ (=1)
void turn(int x,int y)
{
int a,b,c,d;
split(rt,x-1,a,b);
split(b,y-x+1,b,c);
t[b].rev^=1;
rt=merge(a,merge(b,c));
}五、后记
在这里要注意几个点
1.每次拆分子树后,要记得把原树合并回去,一家人就要整整齐齐的
2.上面的操作都是基本操作,都是板子,一些更高深的题可能需要更多操作和打标记,但主要都是灵活运用(split)和(merge)函数,就可以实现很多操作
六、例题
【BZOJ3786】星系探索
深深感到自己的弱小
以上是关于Treap 学习笔记的主要内容,如果未能解决你的问题,请参考以下文章