超难的c语言组合问题

Posted 2023-05-02

1.输入括号的对数n (1<n<10),输出所有的合法组合形式
例:n=3,输出:()()(),(()()),()(()),(())(),

2.输入括号对数n(1<n<30),和嵌套深度m,输出所有合法的组合总数x.

例((()))()(())的嵌套深度是3

回溯吧,反正只有n<10
/*
Name:
Copyright:
Author:
Date: 06-12-08 12:34
Description:
输入括号的对数n (1<n<10),输出所有的合法组合形式
例:n=3,输出:()()(),(()()),()(()),(())(),
*/
#include<iostream>

using namespace std;

void Print(int n);

int main(int argc, char* argv[])

int n;
cin >> n;

Print(n);

system("pause");
return 0;


void Print(int n)

if (n == 0)
cout << " ";
else

for (int i=1; i<=n; i++)

for (int j=0; j<i; j++)//输出i对括号
cout << '(';
for (int j=0; j<i; j++)
cout << ')';

Print(n-i); //输出剩余的括号




第二题是要求输出所有组合，还是只要输出组合个数？ 参考技术A 还真有点难，好好想想 参考技术B 这就是超难？用数据结构栈很容易搞定啊

图解超难理解的 Paxos 算法

引言

上文我们已经详细的阐述了共识问题并介绍了一些共识算法，其中 Paxos 算法是 Leslie Lamport 于 1990 年提出的共识算法，不幸的是采用希腊民主议会的比喻很明显失败了，Lamport 像写小说一样，把一个复杂的数学问题弄成了一篇带有考古色彩的历史小说。根据 Lamport 自己的描述^[1]，三个审稿者都认为该论文尽管并不重要但还有些意思，只是应该把其中所有 Paxos 相关的故事背景删掉。Lamport 对这些缺乏幽默感的人感到生气，所以他不打算对论文做任何修改。

多年后，两个在 SRC(Systems Research Center，DEC 于 1984 年创立，Lamport 也曾在此工作过)工作的人需要为他们正在构建的分布式系统寻找一些合适算法，而 Paxos 恰恰提供了他们想要的。Lamport 就将论文发给他们，他们也没觉得该论文有什么问题。

因此，Lamport 觉得论文重新发表的时间到了，"The Part-Time Parliament^[2]" 最终在 1998 年公开发表。

可是很多人抱怨这篇论文根本看不懂啊，人们只记住了那个奇怪的故事，而不是 Paxos 算法。Lamport 走到哪都要被人抱怨一通。于是他忍无可忍，2001 年重新发表了一篇关于 Paxos 的论文——"Paxos Made Simple^[3]"，这次论文中一个公式也没有，摘要也只有一句话：

The Paxos algorithm, when presented in plain English, is very simple.

满满的都是嘲讽！

然而，可能是表述顺序的原因，这篇论文还是非常难以理解，于是人们写了一系列文章来解释这篇论文（重复造论文），以及在工程上如何实现它。

其中，个人认为讲解 Paxos 最好的视频^[4]来自于 Raft 算法作者 Diego Ongaro，本文采用 Diego 讲义中的图片来理解 Paxos 算法，也纠正了一个个人认为 Diego 笔误的地方。

术语

基本概念

•Proposal Value：提案的值；•Proposal Number：提案编号；•Proposal：提案 = 提案编号 + 提案的值；•Chosen：批准，也叫选定。一旦某个值被 Chosen，后续 Paxos 都必须用该值进行交互。

注：Proposal 有人叫“提议”有人叫“提案”，此处和维基百科里的翻译保持一致，叫“提案”。

角色

•Proposer：提案发起者；•Acceptor：提案接收者；•Learner：提案学习者；

问题描述

为了高可用性，一种常见的设计是用一个 master 节点来写，然后复制到各个 slave 节点。这种解决方法的问题在于，一旦 master 节点故障，整个服务将不可用或者数据不一致。

为了克服单点写入问题，于是有了多数派（Quorum）写，思路就是写入一半以上的节点。即，如果集群中有 N 个节点，客户端需要写入 W >= N/2 + 1 个节点。不需要主节点。这种方法可以容忍最多 (N-1)/2 个节点故障。

但是问题依然存在：每个接收者该如何决定是否接受这次请求的值呢？

如果我们接受第一次收到的值，那么当出现以下情况（Split Votes），则没有出现多数派，没有一个值被 Chosen，算法无法终止，这违反了活性（liveness）。

为了解决 Split Votes 问题，我们允许接受多个不同的值，收到的每一个(every)请求都接受，这时候新的问题出现了，如下，可能不止一个值被 Chosen，这违反了安全性（safety）。

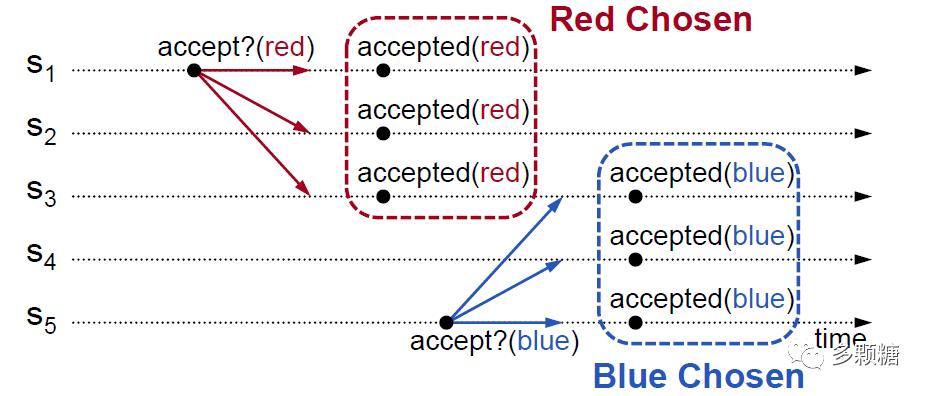
注意，Paxos 强调：

Once a value has been chosen, future proposals must propose the same value.

也就是说，我们讨论的 Basic-Paxos 只会 Chosen 一个值。基于此，就需要一个两阶段（2-phase）协议，对于已经 Chosen 的值，后面的提案也要使用相同的值。

如下图这种情况，S3 直接拒绝 red 值，因为 blue 已经 Chosen，这样就可以保证成功。

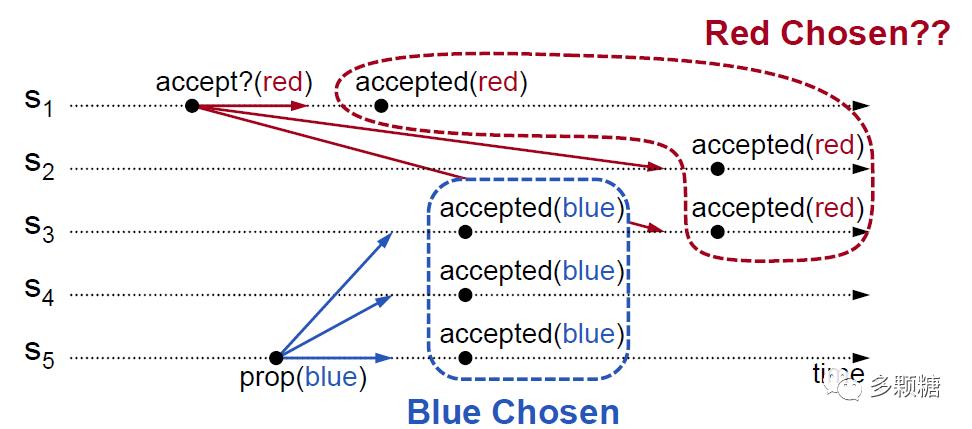
这种方式我们需要对提案进行排序。如果你熟悉分布式系统，应该能想到 "Time, Clocks and the Ordering of Events in a Distributed System^[5]" 这篇论文，我们不能用时间来判断提案的先后顺序。

Proposal Number

一种简单的方式就是每个请求一个唯一的编号，例如：<seq_id, server_id>，为了排序 seq_id 是自增的；同时为了避免崩溃重启，必须能在本地持久化存储。

Paxos

现在我们终于可以开始描述 Paxos 算法了。

如上所述，Paxos 是一个两阶段算法。我们把第一个阶段叫做准备（Prepare）阶段，第二个阶段叫做接受（Accept）阶段。分别对应两轮 RPC。

第一轮 Prepare RPCs：

请求（也叫 Prepare 阶段）：

Proposer 选择一个提案编号 n，向所有的 Acceptor 广播 Prepare(n) 请求。

这里 Prepare（n）不包含提案的值。

伪代码：

send PREPARE(++n)

响应（也叫 PROMISE 阶段）：

Acceptor 接收到 Prepare（n) 请求，此时有两种情况：

•如果 n 大于之前接受到的所有 Prepare 请求的编号，则返回 Promise() 响应，并承诺将不会接收编号小于 n 的提案。如果有提案被 Chosen 的话，Promise() 响应还应包含前一次提案编号和对应的值。•否则（即 n 小于等于 Acceptor 之前收到的最大编号）忽略，但常常会回复一个拒绝响应。

所以，Acceptor 需要持久化存储 max_n、accepted_N 和 accepted_VALUE

伪代码：

if (n > max_n) max_n = n // save highest n we've seen so far if (proposal_accepted == true) // was a proposal already accepted? respond: PROMISE(n, accepted_N, accepted_VALUE) else respond: PROMISE(n)else do not respond (or respond with a "fail" message)

第二轮 Accept RPCs：

请求（也叫 PROPOSE 阶段）：

当 Proposer 收到超过半数 Acceptor 的 Promise() 响应后，Proposer 向多数派的 Acceptor 发起 Accept(n, value) 请求并带上提案编号和值。（注：这里讲义的算法流程图是向所有的 Acceptor 发起 Accept() 请求，鄙人认为应该改为向多数派 Acceptor 发起。）

注意：Proposer 不一定是将 Accept() 请求发给有应答的多数派 Acceptors，可以再选另一个多数派 Acceptors 广播 Accept() 请求。

关于值 value 的选择：如果前面的 Promise 响应有返回 accepted_VALUE，那就使用这个值作为 value。如果没有返回 accepted_VALUE，那可以自由决定提案值 value。

伪代码：

did I receive PROMISE responses from a majority of acceptors?if yes do any responses contain accepted values (from other proposals)? if yes val = accepted_VALUE // value from PROMISE message with the highest accepted ID if no val = VALUE // we can use our proposed value send Accept(ID, val) to at least a majority of acceptors

响应（也叫 ACCEPT 阶段）：

Acceptor 收到 Accept() 请求，在这期间如果 Acceptor 没有对比 n 更大的编号另行 Promise，则接受该提案。

伪代码：

if (n >= max_n) // is the n the largest I have seen so far? proposal_accepted = true // note that we accepted a proposal accepted_N = n // save the accepted proposal number accepted_VALUE = VALUE // save the accepted proposal data respond: Accepted(N, VALUE) to the proposer and all learnerselse do not respond (or respond with a "fail" message)

一些例子

情况 1：提案已 Chosen

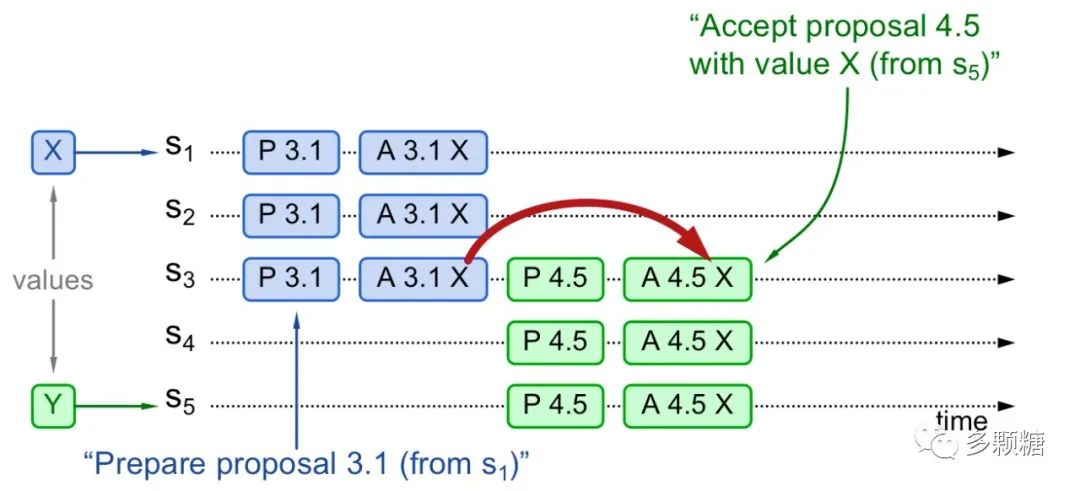
1.S1 收到客户端提案请求 X，于是 S1 向 S1-S3 发起 Prepare(3.1) 请求，PROMISE() 响应返回没有提案被 Chosen2.由于 S1-S3 没有任何提案被 Chosen，S1 继续向 S1-S3 发送 Accept(3.1, X) 请求，提案被成功 Chosen3.在提案被 Chosen 后，S5 收到客户端提案值为 Y 的请求，向 S3-S5 发送 Prepare(4.5) 请求，由于编号 4 > 3 会收到提案值为 X 已经被 Chosen 的 PROMISE() 响应4.于是 S5 将提案值 Y 替换成 X，向 S1-S3 发送 Accept(4.5, X) 请求，提案再次被 Chosen

情况 2：提案未 Chosen，Proposer 可见

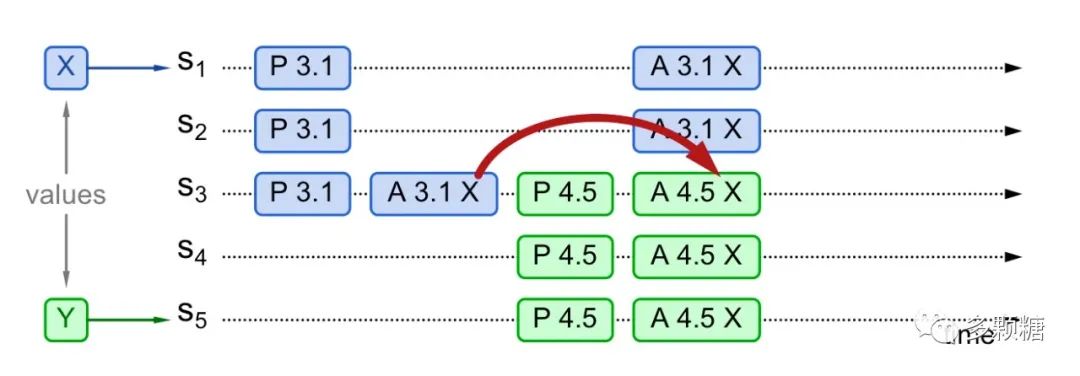
情况 2 和情况 1 类似，在 S3 Chosen 了提案后，S5 收到来自 S3 的 PROMISE() 响应包含了已经 Chosen 的提案值 X，所以同样会将提案值替换成 X，最终所有 Acceptor 对 X 达成共识。

注意上面的伪代码：do any responses contain accepted values，也就是说只要有一个 Acceptor 在 Promise() 响应中返回了提案值，就要用它来替换提案值。

情况 3：提案未提交，Proposer 不可见

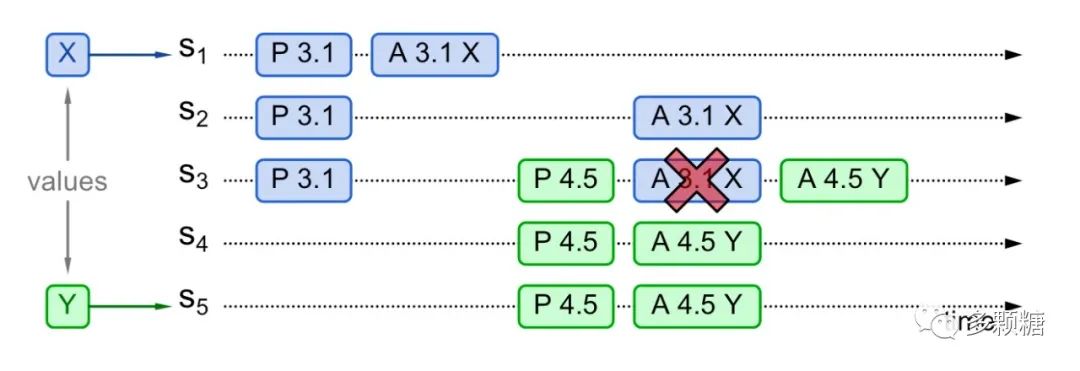
情况 3 中，提案只被 S1 Chosen，S3 还未 Chosen 该提案，S3-S5 的 Promise() 响应中没有任何提案信息，所以 S5 自行决定提案值为 Y，发送 Accept(4.5, Y) 请求。

由于此时 S3 承诺的提案编号 n 变为了 4 且 4 大于 3，所以 S3 不再接受 S1 后续的 Accept(3.1, X) 请求。提案值 X 被阻止，而提案值 Y 最终被 Chosen。

活锁

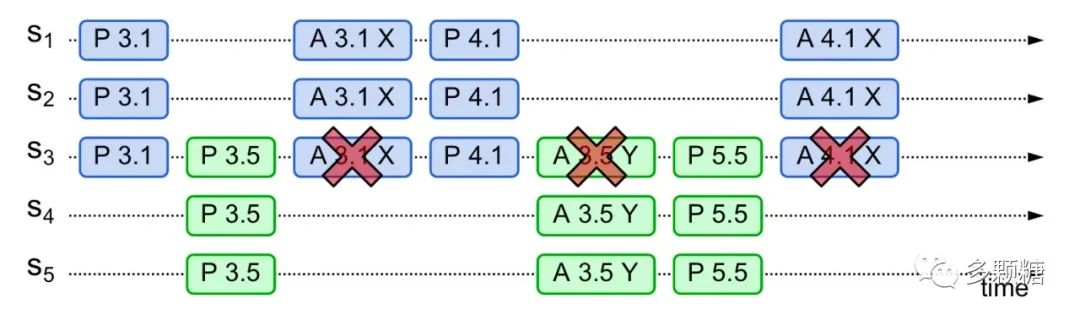
如图：当 Proposer 在第一轮 Prepare 发出请求，还没来得及后续的第二轮 Accept 请求，紧接着第二个 Proposer 在第一阶段也发出编号更大的请求。如果这样无穷无尽，Acceptor 始终停留在决定顺序号的过程上，那大家谁也成功不了。

解决活锁最简单的方式就是引入随机超时，这样可以让某个 Proposer 先进行提案，减少一直互相抢占的可能。

结语

Paxos 只从一个或多个值中选择一个值，如果需要重复运行 Paxos 来创建复制状态机，我们称之为 multi-Paxos，但如果每个命令都通过一个Basic Paxos算法实例来达到一致，会产生大量开销。对于 multi-Paxos 可以做一些优化，我们在下篇文章中讨论 Paxos 的变种。

References

[1] Lamport 自己的描述: http://lamport.azurewebsites.net/pubs/pubs.html#lamport-paxos
[2] The Part-Time Parliament: https://lamport.azurewebsites.net/pubs/lamport-paxos.pdf
[3] Paxos Made Simple: https://lamport.azurewebsites.net/pubs/paxos-simple.pdf
[4] 视频: https://www.youtube.com/watch?v=JEpsBg0AO6o
[5] Time, Clocks and the Ordering of Events in a Distributed System: http://lamport.azurewebsites.net/pubs/time-clocks.pdf

---

推荐阅读

• 
  

福利

我为大家整理了一份从入门到进阶的Go学习资料礼包（下图只是部分），同时还包含学习建议：入门看什么，进阶看什么。

关注公众号 「polarisxu」，回复  ebook  获取；还可以回复「进群」，和数万 Gopher 交流学习。