遗传算法 交叉的个数怎么确定

（1）初识遗传算法

        遗传算法，模拟达尔文进化论的自然选择和遗传学机理的生物进化过程的计算模型，一种选择不断选择优良个体的算法。谈到遗传，想想自然界动物遗传是怎么来的，自然主要过程包括染色体的选择，交叉，变异（不明白这个的可以去看看生物学），这些操作后，保证了以后的个体基本上是最优的，那么以后再继续这样下去就可以一直最优了。

（2）解决的问题

        先说说自己要解决的问题吧。遗传算法很有名，自然能解决的问题很多了，在原理上不变的情况下，只要改变模型的应用环境和形式，基本上都可以。但是遗传算法主要还是解决优化类问题，尤其是那种不能直接解出来的很复杂的问题，而实际情况通常也是这样的。

本部分主要为了了解遗传算法的应用，选择一个复杂的二维函数来进行遗传算法优化。函数显示为y=10*sin(5*x)+7*abs(x-5)+10，这个函数图像为：

　　怎么样，还是有点复杂的吧，当然你还可以任意假设和编写，只要符合就可以。那么现在问你要你一下求出最大值你能求出来吗？（这个貌似可以，很容易看出来---如何再复杂一点估计就不行了）这类问题如果用遗传算法或者其他优化方法就很简单了，为什么了，说白了，其实就是计算机太笨，同时计算速度又超快，举个例子吧，我把x等分为100万份，再一下子都带值进去算，求出对应的100万个y的值，再比较他们的大小找到最大值不久可以了么，很笨吧，人算是不可能的，但是计算机可以。而遗传算法也是很笨的一个个搜索，只不过加了一点什么了，就是人为的给它算的方向与策略，让它有目的的算，这也就是算法了。扯多了，正题吧。。。

（3）如何开始

        不明白的遗传算法的会问怎么开始呢？恩，其实每个算法都有自己开始的方式，遗传算法也是。首先是选择个体了。我们知道一个种群中可能只有一个人吗？不可能吧，肯定很多人才对，这样相互结合的机会才多，产生的后代才会多种多样，才会有更好的优良基因，有利于种群的发展。那么算法也是如此，当然个体多少是个问题，一般来说20-100之间我感觉差不多了。那么个体究竟是什么了？在我们这个问题中，自然就是x值了，其他情况下，个体就是所求问题的变量，这里我们假设个体数选100个，也就是开始选了100个不同的x值，不明白的话就假设是100个猴子吧。好了现在有了100个猴子组成的一个种群，那么这个种群该怎么发展才能越来越好了？说到这，我们想想，如何去定义这个越来越好呢？这该有个评价指标吧，在我们这个题中，好像是对于的y值越大越好是吧，也就是说哪些x对应的y值越大，我们就认为这个x越好，对于不同的x值，在把他们的y值确定后，我们甚至可以给他们排个名来决定哪些好些。我们把这个叫做对于个体的适应度，这应该算是算法的后半部分才对。

（4）编码

         首先明白什么是编码？为什么要编码？如何编码？

        好，什么是编码？其实编码就是把自变量（x）换一个形式而已，在这个形式下，更容易操作其他过程（比如交叉、变异什么的）而已。举个例子吧，假如我们取x=1，2,3，我可以把x编码成x=a，b，c，我就说123对应的就是abc，为什么要这样做呢，比如问题里面你能够获取的都是abc组合之类的，那么这样编码以后，你就可以再返回去成123来操作了。一般的编码都有些什么了？二进制编码，自然数编码，矩阵编码。。很多，不详写了。而用的最多的可以说是二进制编码吧，感觉这和人体DNA、基因的排列很相似，想想DNA怎么排的？不就是在两条长链上一对一排的吗？那么什么是二进制编码？很简单，就是1、0、1、0对应的来回组合排列而已。比如：1100100010,   0011001001  等等，这些都是位数长度为10的二进制编码。再想想1在计算机的二进制形式是多少？如果以八位来表示的话，是不是就是：0000 0001 ；8是不是就是0000 1000；以此类推，那么我们这里也是这样，把对应的x值换算成这种编码形式，我们这里可以看到x的范围是0~5吧，如何照计算机这样的方式，是不是到0000 0101 这里就完事了？想想这样多短，前面五位都没有用上多浪费呀，那么要想都用上怎么办了？也很简单，我们把0000 0001 不认为是1不就可以了吗？因为1111 1111 为255，那么如果说每一份为1/255的话，那么0000 0001不就是1/255（不是1了，比1小很多了），这个时候1怎样表示了？不就是：1111 1111了。好了我们把范围扩大一些吧，每一份不是1/255, 而是1/255*5,那么这个时候最大值是多少？是不是5，恩，这样x编码的范围不就在0~5之间了吗。这里就又有问题了，想想这样的话x最小精度为多少？就是1/255*5，虽然很小，但是在0~1/255*5之间的x你能不能取到？无论如何都不能吧，那么就又来了一个问题，怎样去增大这个精度呢？如果要保持0~5不变的话，只能增加位数了，把8位编码变成10位，20位，100位，哇，够大了吧，变成了100个0、1组合，很恐怖吧，事实上究竟是多少要视情况来定，一般20左右感觉就可以了，虽然说越大越好，但是太大了耗内存呀，速度慢了，不值。本题中，我们设置它为一个变量，先暂时取为10来实验。好了，如果还不明白为什么要编码看下面的吧，知道了交叉与变异，你就知道了。

（5）关于交叉与变异

        先说变异吧，什么是变异？简单，基因发生了突变就叫变异。有了编码的概念，那就在编码的基础上来说变异了。首先就讲最简单的变异，单个点的变异。现在以10位长度的编码来说，比如把x=3编码一下，随便假设为11000 10010吧，好了在变异操作时，假设第5位变异了（说一下变异就是对应一位或者多位0或1变成1或0，也只能在0,1之间变，没办法呀），那么这个时候变成什么了？是不是为11001 10010（把前面的认为低位，和计算机里面的不一样了，自己定义而已吧），好了现在看看现在11001 10010 再反编码回去成x是多少呢？那肯定不是3了，变了呀，是多少肯定可以反算回去了，这里懒得算了，就假设为3.213吧，发没发现，这样一来，x是不是变了？既然变了就好呀，带到原函数（适应度函数）里面去比较这两个x值对应的那个y值大一些，如何后面变异后的大些是不是就是说产生了好的变异呀，就可以在下一次个体选择的时候选择它了。那么想想很多x来一起变异会怎么样了？肯定会生成很多好的解吧，反复这样做又会怎么样了？只要每次都保留最优解的话，我来循环个100万次，也总能找到最优解吧，当然这么多次得花多久，也不合适。这还只是一个点位在进行变异，如果每次我让多个点位变异呢？哇，又不可思议了，变化更大了吧。当然，变异不止如此，更多的去看专业论文吧，知道了变异是干什么的，剩下的都好说了吧。好了，这还只是变异，想想自然界遗传中除了变异还有什么，交叉吧，那么交叉又是什么了？

　　学过生物的都知道，动物交配时，部分染色体干什么了，是不是交叉了？就是把相应部分的基因交换了，你的给了我，我的给了你，很有爱吧。再以编码为例吧，比如现在随便从100个x值中选取两个吧，假设正好选中了x=3和4，对应的编码假设是：11001 10101和00101 01011，那么怎么交叉呢？我们知道每次交叉的染色体通常是不是一块一块的？恩，这里在算法设计上也来一块一块的吧，比如说就把位置在2,3,4号的编码给整体交叉了吧，那么x=3对应位置是100吧，x=4对应位置是010吧，好，交换以后x=3对应位置就变成了010，而x=4就变成了100，加回去就变成了什么了？X=3是不是就为10101 10101，x=4是不是就为01001 01011了。而现在，把他们再反编码回去还是x=3,4吗？显然又不是了吧（当然也有概率是一样的吧，很小）。那是什么了？不想算，还是假设吧，假设为3.234,和4.358把，好了新的个体是不是又来了？恩，同理，带到适应度函数里面去吧，在取优秀个体，完事。同样，有些专门研究这种算法的开发出来各种各样的交叉方式，什么一个个体的前3个与后一个个体的后3个交叉，中间几位来交叉等等，总之就是生产新个体，而这样做的目的在哪了？无非是三个字，随机性，充分保证生产新个体具有随机性，你说你的x=3变异后为3.2,3.1什么的距离3那么近，在一些存在局部最优解问题上就永远跳不出局部最优解，相反，你的x=1一下子变异成了x=5，哇，好大的变化呀，一下从这头到了那头，这对于算法的广阔搜索能力来说是非常好的。

　　讲完了这部分，现在知道了为什么要编码了吧？如果你不编码，你说你想要你的x=3怎么去变异，怎么去交叉？当然也不是没有方法，比如你生成一个小的随机数加到x=3上，但是你想想这两种方法哪一个更具有随机性、普遍性？显然的。而更多的时候交叉与变异是在一起操作的，先交叉，再变异（或者反过来）是普遍遗传算法的操作步骤。

（6）关于选择的问题

        说完了上面的部分，在说说选择吧，选择是什么？就是优胜劣汰。好的留下来，差的走人，在自然界中直接gg了是吧。所以才有了人类这种高级动物。不停的选择使得种群一直朝着较好的方向行走。

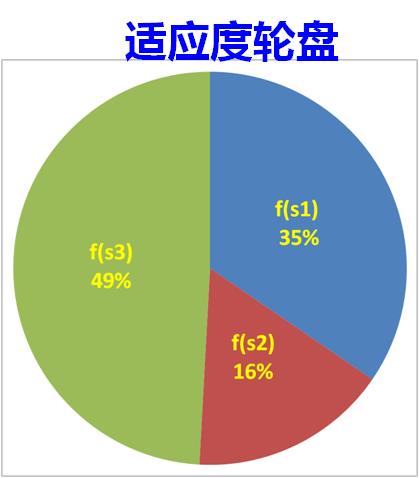
        对应到本问题来说，遗传算法的选择是什么样子的呢？在前面说到，每次交叉或者变异是不是产生了新的个体？如果这些个体都保留下来的话，种群是要爆炸的，第一次循环可能有100个x，第二次就200个，再来那么10万次循环，哇哦，多少了，好多。显然不可能吧，而且在算法里面，我们还规定的是每次循环都必须保证都是100个个体，那么必须在200个个体中剔除100个吧，好了，问题来了，如何剔除呢？有人说很简单，排名吧，取前100号x不久可以了吗？排名这个东西真的准吗？我就不信，凭什么差一点的不能选上，搞不好在下一次变异中一下子冲到了第一呢？这个问题在选择上也有一些对应的规则，最通用的就是轮盘赌法，简单来说就是一种概率选择法（当然还有许多其他的方法，感兴趣自己搜相关的文献吧，我也没用过）。什么是轮盘赌法呢？就是把对应所有y值（适应度函数值）加起来，再用各自的y值去除以这个sum值，这样是不是谁的概率大谁的概率小就很清楚了？然后再随机生成一个0~1的概率值p，谁在p的范围里面是不是就选择谁，比如说x=3时在100个x中y的值最大，那么选择它的概率是不是就最大，比如说是0.1（0.1小吗？不小了好吧，想想其他的会是什么，都比0.1小，那么从概率上讲，选100次的话，是不是就有10次选到了x=3，其他的都不足10次是吧，那么在下一次100个种群个体中就有10个x=3了，再来一回可能就有20个x=3了，再就是30个，最最后就只剩下100个x=3，它自己在那里交叉变异是不是已经没什么意义了，如果到了这个时候就意味着这个算法可以结束了）。再详细点，如下图所示吧：现在要在下面三个大类中先去100个x个体，轮盘赌转100次以后，是不是个体数落在s3中的个体多一些，选择的原理就是这样，再不明白直接后面的程序吧，我曾经也研究了好久。。。

（7）还差点什么呢

        至此，感觉也差不多了吧，选择完后再重复上述步骤交叉、变异等等。那么什么时候是个头了？很简单办法就是迭代次数，迭代10次看一下结果，20次，30次，100次，当次数达到一定程度以后，优秀的个体越来越多，大都集中在最优解附近，即使变异或者交叉了也是在这个最优解附近，没有影响的，在下一次选择后就有变回来了。那么至此就真的结束了。比如说先来结果吧，该问题按我这个思路做完后，迭代100次变成什么样子了？上图如下：

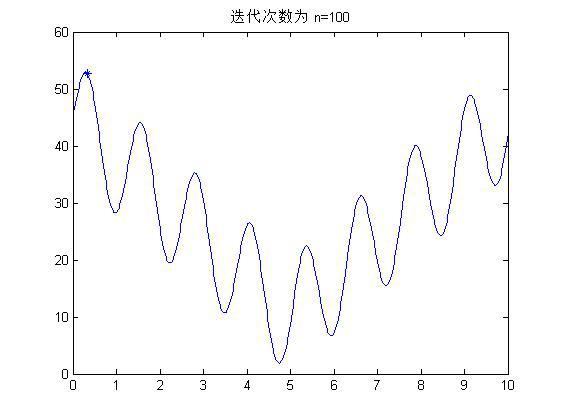
         看看，所有的解（100个）都集中在了x=0.286附近是吧，也就是基本上达到最优解了。