遗传算法的运算过程

Posted 2023-05-02

遗传操作是模拟生物基因遗传的做法。在遗传算法中，通过编码组成初始群体后，遗传操作的任务就是对群体的个体按照它们对环境适应度(适应度评估)施加一定的操作，从而实现优胜劣汰的进化过程。从优化搜索的角度而言，遗传操作可使问题的解，一代又一代地优化，并逼近最优解。
遗传操作包括以下三个基本遗传算子(genetic operator):选择(selection)；交叉(crossover)；变异(mutation)。这三个遗传算子有如下特点：
个体遗传算子的操作都是在随机扰动情况下进行的。因此，群体中个体向最优解迁移的规则是随机的。需要强调的是，这种随机化操作和传统的随机搜索方法是有区别的。遗传操作进行的高效有向的搜索而不是如一般随机搜索方法所进行的无向搜索。
遗传操作的效果和上述三个遗传算子所取的操作概率，编码方法，群体大小，初始群体以及适应度函数的设定密切相关。 从群体中选择优胜的个体，淘汰劣质个体的操作叫选择。选择算子有时又称为再生算子(reproduction operator)。选择的目的是把优化的个体(或解)直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的，目前常用的选择算子有以下几种：适应度比例方法、随机遍历抽样法、局部选择法。
其中轮盘赌选择法 （roulette wheel selection）是最简单也是最常用的选择方法。在该方法中，各个个体的选择概率和其适应度值成比例。设群体大小为n，其中个体i的适应度为，则i 被选择的概率，为遗传算法
显然，概率反映了个体i的适应度在整个群体的个体适应度总和中所占的比例。个体适应度越大。其被选择的概率就越高、反之亦然。计算出群体中各个个体的选择概率后，为了选择交配个体，需要进行多轮选择。每一轮产生一个[0，1]之间均匀随机数，将该随机数作为选择指针来确定被选个体。个体被选后，可随机地组成交配对，以供后面的交叉操作。 在自然界生物进化过程中起核心作用的是生物遗传基因的重组(加上变异)。同样，遗传算法中起核心作用的是遗传操作的交叉算子。所谓交叉是指把两个父代个体的部分结构加以替换重组而生成新个体的操作。通过交叉，遗传算法的搜索能力得以飞跃提高。
交叉算子根据交叉率将种群中的两个个体随机地交换某些基因，能够产生新的基因组合，期望将有益基因组合在一起。根据编码表示方法的不同，可以有以下的算法：
a)实值重组（real valued recombination）
1)离散重组（discrete recombination）
2)中间重组（intermediate recombination）
3)线性重组（linear recombination）
4)扩展线性重组（extended linear recombination）。
b)二进制交叉（binary valued crossover）
1)单点交叉（single-point crossover）
2)多点交叉（multiple-point crossover）
3)均匀交叉（uniform crossover）
4)洗牌交叉（shuffle crossover）
5)缩小代理交叉（crossover with reduced surrogate）。
最常用的交叉算子为单点交叉(one-point crossover)。具体操作是:在个体串中随机设定一个交叉点，实行交叉时，该点前或后的两个个体的部分结构进行互换，并生成两个新个体。下面给出了单点交叉的一个例子：
个体A：1 0 0 1 ↑1 1 1 → 1 0 0 1 0 0 0 新个体
个体B：0 0 1 1 ↑0 0 0 → 0 0 1 1 1 1 1 新个体 变异算子的基本内容是对群体中的个体串的某些基因座上的基因值作变动。依据个体编码表示方法的不同，可以有以下的算法：
a)实值变异
b)二进制变异。
一般来说，变异算子操作的基本步骤如下：
a)对群中所有个体以事先设定的变异概率判断是否进行变异
b)对进行变异的个体随机选择变异位进行变异。
遗传算法引入变异的目的有两个:一是使遗传算法具有局部的随机搜索能力。当遗传算法通过交叉算子已接近最优解邻域时，利用变异算子的这种局部随机搜索能力可以加速向最优解收敛。显然，此种情况下的变异概率应取较小值，否则接近最优解的积木块会因变异而遭到破坏。二是使遗传算法可维持群体多样性，以防止出现未成熟收敛现象。此时收敛概率应取较大值。
遗传算法中，交叉算子因其全局搜索能力而作为主要算子，变异算子因其局部搜索能力而作为辅助算子。遗传算法通过交叉和变异这对相互配合又相互竞争的操作而使其具备兼顾全局和局部的均衡搜索能力。所谓相互配合.是指当群体在进化中陷于搜索空间中某个超平面而仅靠交叉不能摆脱时，通过变异操作可有助于这种摆脱。所谓相互竞争，是指当通过交叉已形成所期望的积木块时，变异操作有可能破坏这些积木块。如何有效地配合使用交叉和变异操作，是目前遗传算法的一个重要研究内容。
基本变异算子是指对群体中的个体码串随机挑选一个或多个基因座并对这些基因座的基因值做变动(以变异概率P.做变动)，(0，1)二值码串中的基本变异操作如下：
基因位下方标有*号的基因发生变异。
变异率的选取一般受种群大小、染色体长度等因素的影响，通常选取很小的值，一般取0.001－0.1。 当最优个体的适应度达到给定的阈值，或者最优个体的适应度和群体适应度不再上升时，或者迭代次数达到预设的代数时，算法终止。预设的代数一般设置为100-500代。

参考技术A 在投资早餐加盟店以后

matlab遗传算法工具箱

转自http://blog.sina.com.cn/s/blog_5ebcc0240101pnrj.html

matlab遗传算法工具箱函数及实例讲解

(2014-01-10 13:03:57)

分类： matlab

最近研究了一下遗传算法，因为要用遗传算法来求解多元非线性模型。还好用遗传算法的工具

箱予以实现了，期间也遇到了许多问题。借此与大家分享一下。

首先，我们要熟悉遗传算法的基本原理与运算流程。

基本原理：遗传算法是一种典型的启发式算法，属于非数值算法范畴。它是模拟达尔文的自然

选择学说和自然界的生物进化过程的一种计算模型。它是采用简单的编码技术来表示各种复杂

的结构，并通过对一组编码表示进行简单的遗传操作和优胜劣汰的自然选择来指导学习和确定

搜索的方向。遗传算法的操作对象是一群二进制串（称为染色体、个体），即种群，每一个染

色体都对应问题的一个解。从初始种群出发，采用基于适应度函数的选择策略在当前种群中选

择个体，使用杂交和变异来产生下一代种群。如此模仿生命的进化进行不断演化，直到满足期

望的终止条件。

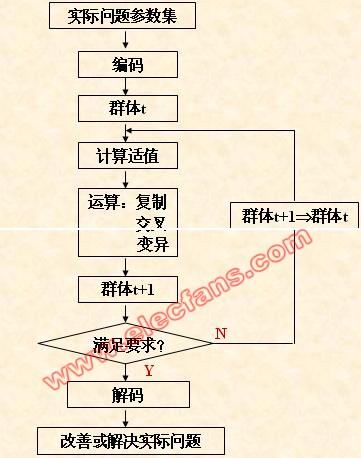
运算流程：

Step 1：对遗传算法的运行参数进行赋值。参数包括种群规模、变量个数、交叉概率、变异概

率以及遗传运算的终止进化代数。

Step 2：建立区域描述器。根据轨道交通与常规公交运营协调模型的求解变量的约束条件，设

置变量的取值范围。

Step 3：在Step 2的变量取值范围内，随机产生初始群体，代入适应度函数计算其适应度值。

Step 4：执行比例选择算子进行选择操作。

Step 5：按交叉概率对交叉算子执行交叉操作。

Step 6：按变异概率执行离散变异操作。

Step 7：计算Step 6得到局部最优解中每个个体的适应值，并执行最优个体保存策略。

Step 8：判断是否满足遗传运算的终止进化代数，不满足则返回Step 4，满足则输出运算结果

。

 

其次，运用遗传算法工具箱。

 

运用基于Matlab的遗传算法工具箱非常方便，遗传算法工具箱里包括了我们需要的各种函数库

。目前，基于Matlab的遗传算法工具箱也很多，比较流行的有英国设菲尔德大学开发的遗传算

法工具箱GATBX、GAOT以及Math Works公司推出的GADS。实际上，GADS就是大家所看到的

Matlab中自带的工具箱。我在网上看到有问为什么遗传算法函数不能调用的问题，其实，主要

就是因为用的工具箱不同。因为，有些人用的是GATBX带有的函数，但MATLAB自带的遗传算法

工具箱是GADS，GADS当然没有GATBX里的函数，因此运行程序时会报错，当你用MATLAB来编写

遗传算法代码时，要根据你所安装的工具箱来编写代码。

 

以GATBX为例，运用GATBX时，要将GATBX解压到Matlab下的toolbox文件夹里，同时，set path

将GATBX文件夹加入到路径当中。

 

最后，编写Matlab运行遗传算法的代码。

 

这块内容主要包括两方面工作：1、将模型用程序写出来（.M文件），即目标函数，若目标函

数非负，即可直接将目标函数作为适应度函数。2、设置遗传算法的运行参数。包括：种群规

模、变量个数、区域描述器、交叉概率、变异概率以及遗传运算的终止进化代数等等。

 

为方便大家理解，以下为例：

求解模型：TC=x1+2*x2+3*x3+4*x4，-1<=x<=0

根据上面的求解模型，可以写出模型的.M文件如下，即适应度函数

function TC=TotalCost(x)
TC=0;
for i=1:4
TC=TC+i*x(i);
end

然后，可以利用遗传算法工具箱来写出遗传算法运行的主要程序，如下：

%定义遗传算法参数
NIND=20;                   %个体数目
MAXGEN=200;                %最大遗传代数
NVAR=4;                   %变量维数
PRECI=20;                  %变量的二进制位数
GGAP=0.9;                  %代沟
trace=zeros(MAXGEN,2);     %算法性能跟踪
%建立区域描述器
FieldD=[rep(PRECI,[1,NVAR]);rep([-1;0],[1,NVAR]);rep([1;0;1;1],[1,NVAR])];
Chrom=crtbp(NIND,NVAR*PRECI);                               %创建初始种群
gen=0;                                                      %代计数器
ObjV=TotalCost(bs2rv(Chrom,FieldD));                        %计算初始种群个体的目

标函数值
while gen
   FitnV=ranking(ObjV);                                     %分配适应度值
   SelCh=select(‘sus‘,Chrom,FitnV,GGAP);                    %选择
   SelCh=recombin(‘xovsp‘,SelCh,0.7);                       %重组
   SelCh=mut(SelCh,0.07);                                   %变异
   ObjVSel=TotalCost(bs2rv(SelCh,FieldD));                  %计算子代目标函数值
   [Chrom ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel);        %重插入
   gen=gen+1;
   %输出最优解及其对应的10个变量的十进制值
   [Y,I]=min(ObjVSel);
   Y,X=bs2rv(Chrom(I,:),FieldD);
   trace(gen,1)=min(ObjV);
   trace(gen,2)=sum(ObjV)/length(ObjV);
end
plot(trace(:,1));hold on;
plot(trace(:,2),‘-.‘);grid;
legend(‘种群均值的变换‘,‘最优解的变化‘);

显然，根据模型的特征，最优解应该是-10，自变量分别取-1，-1，-1，-1。大家可以安装

GATBX，在Matlab中建立目标函数的.M文件以及遗传算法主程序的文件来进行试验。

 

希望以上内容对学习和运用遗传算法的同仁有所帮助，因为本人也是初学，因此有不详之处请

见谅。

////////////////////////////////////////////////////
matlab遗传算法工具箱函数及实例讲解（转引）  
gaotv5

核心函数： 
(1)function [pop]=initializega(num,bounds,eevalFN,eevalOps,options)--初始种群的生

成函数 
【输出参数】 
 pop--生成的初始种群 
【输入参数】 
 num--种群中的个体数目 
 bounds--代表变量的上下界的矩阵 
 eevalFN--适应度函数 
 eevalOps--传递给适应度函数的参数 
 options--选择编码形式(浮点编码或是二进制编码)[precision F_or_B],如 
    precision--变量进行二进制编码时指定的精度 
    F_or_B--为1时选择浮点编码，否则为二进制编码,由precision指定精度)

(2)function [x,endPop,bPop,traceInfo] = ga(bounds,evalFN,evalOps,startPop,opts,... 
         termFN,termOps,selectFN,selectOps,xOverFNs,xOverOps,mutFNs,mutOps)--遗传

算法函数 
【输出参数】 
    x--求得的最优解 
    endPop--最终得到的种群 
    bPop--最优种群的一个搜索轨迹 
【输入参数】 
    bounds--代表变量上下界的矩阵 
    evalFN--适应度函数 
    evalOps--传递给适应度函数的参数 
    startPop-初始种群 
    opts[epsilon prob_ops display]--opts(1:2)等同于initializega的options参数，第三

个参数控制是否输出，一般为0。如[1e-6 1 0] 
    termFN--终止函数的名称,如[‘maxGenTerm‘] 
    termOps--传递个终止函数的参数,如[100] 
    selectFN--选择函数的名称,如[‘normGeomSelect‘] 
    selectOps--传递个选择函数的参数,如[0.08] 
    xOverFNs--交叉函数名称表，以空格分开，如[‘arithXover heuristicXover

simpleXover‘] 
    xOverOps--传递给交叉函数的参数表，如[2 0;2 3;2 0] 
    mutFNs--变异函数表，如[‘boundaryMutation multiNonUnifMutation nonUnifMutation

unifMutation‘] 
    mutOps--传递给交叉函数的参数表,如[4 0 0;6 100 3;4 100 3;4 0 0]

注意】matlab工具箱函数必须放在工作目录下 
【问题】求f(x)=x+10*sin(5x)+7*cos(4x)的最大值，其中0<=x<=9 
【分析】选择二进制编码，种群中的个体数目为10，二进制编码长度为20，交叉概率为0.95,

变异概率为0.08 
【程序清单】 
   %编写目标函数 
     function[sol,eval]=fitness(sol,options) 
       x=sol(1); 
       eval=x+10*sin(5*x)+7*cos(4*x); 
   %把上述函数存储为fitness.m文件并放在工作目录下 
    
   initPop=initializega(10,[0 9],‘fitness‘);%生成初始种群，大小为10 
   [x endPop,bPop,trace]=ga([0 9],‘fitness‘,[],initPop,[1e-6 1

1],‘maxGenTerm‘,25,‘normGeomSelect‘,... 
     [0.08],[‘arithXover‘],[2],‘nonUnifMutation‘,[2 25 3]) %次遗传迭代

运算借过为：x = 
   7.8562 24.8553(当x为7.8562时，f（x）取最大值24.8553)

注：遗传算法一般用来取得近似最优解，而不是最优解。

遗传算法实例2

【问题】在－5<=Xi<=5,i=1,2区间内，求解 
       f(x1,x2)=-20*exp(-0.2*sqrt(0.5*(x1.^2+x2.^2)))-exp(0.5*(cos(2*pi*x1)+cos

(2*pi*x2)))+22.71282的最小值。 
【分析】种群大小10，最大代数1000，变异率0.1,交叉率0.3 
【程序清单】 
   ％源函数的matlab代码 
      function [eval]=f(sol) 
        numv=size(sol,2); 
        x=sol(1:numv); 
        eval=-20*exp(-0.2*sqrt(sum(x.^2)/numv)))-exp(sum(cos(2*pi*x))/numv)

+22.71282; 
  %适应度函数的matlab代码 
      function [sol,eval]=fitness(sol,options) 
        numv=size(sol,2)-1; 
        x=sol(1:numv); 
        eval=f(x); 
        eval=-eval; 
  %遗传算法的matlab代码 
      bounds=ones(2,1)*[-5 5]; 
      [p,endPop,bestSols,trace]=ga(bounds,‘fitness‘)