时间序列模式（ARIMA）---Python实现

Posted 2020-12-05 蜘蛛侠不会飞

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了时间序列模式（ARIMA）---Python实现相关的知识，希望对你有一定的参考价值。

时间序列分析的主要目的是根据已有的历史数据对未来进行预测。如餐饮销售预测可以看做是基于时间序列的短期数据预测，预测的对象时具体菜品的销售量。

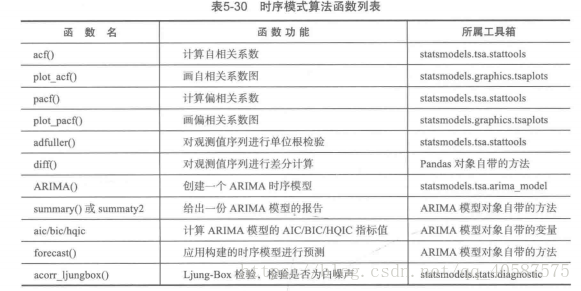
1.时间序列算法：

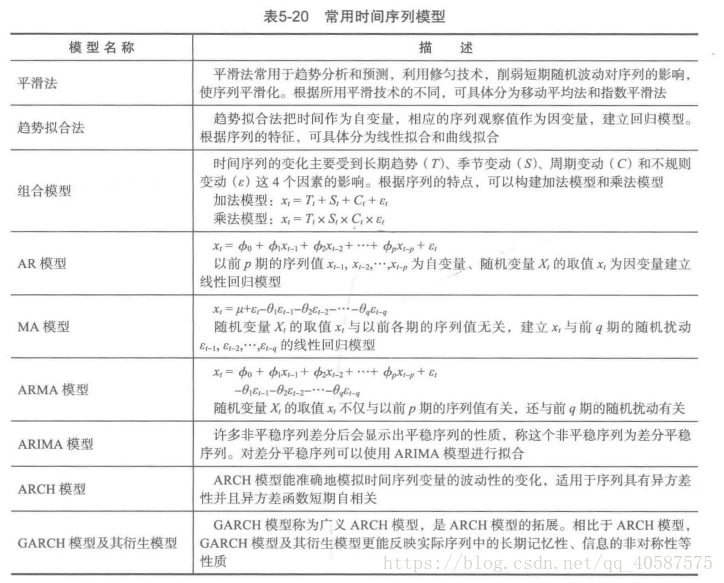
常见的时间序列模型;

技术分享图片 ?

2.时序模型的预处理

1. 对于纯随机序列，也称为白噪声序列，序列的各项之间没有任何的关系，序列在进行完全无序的随机波动，可以终止对该序列的分析。

2. 对于平稳非白噪声序列，它的均值和方差是常数。ARMA 模型是最常用的平稳序列拟合模型。

3. 对于非平稳序列，由于它的方差和均值不稳定，处理方法一般是将其转化成平稳序列。可以使用ARIMA 模型进行分析。

对平稳性的检验：

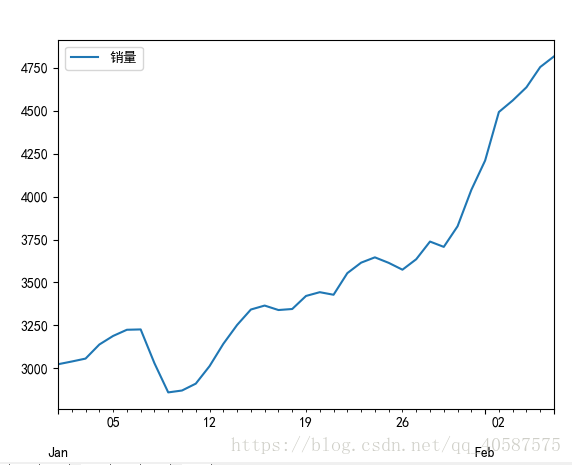
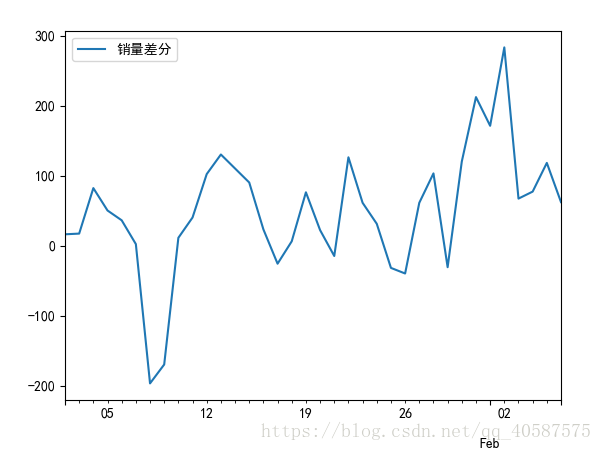
1.时序图检验：根据平稳时间序列的均值和方差都是常数的特性，平稳序列的时序图显示该序列值时钟在一个参数附近随机波动，而且波动的范围是有界的。如果有明显的趋势或者周期性，那它通常不是平稳序列。

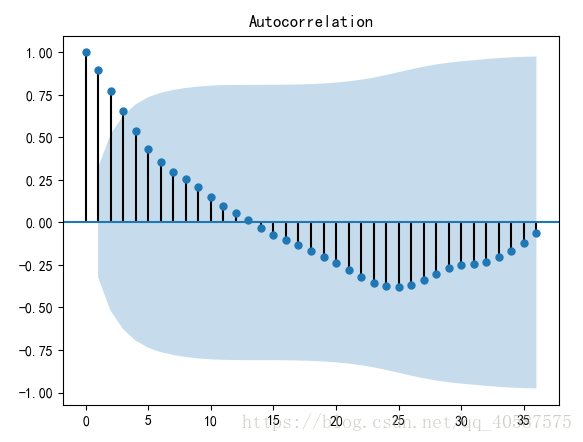
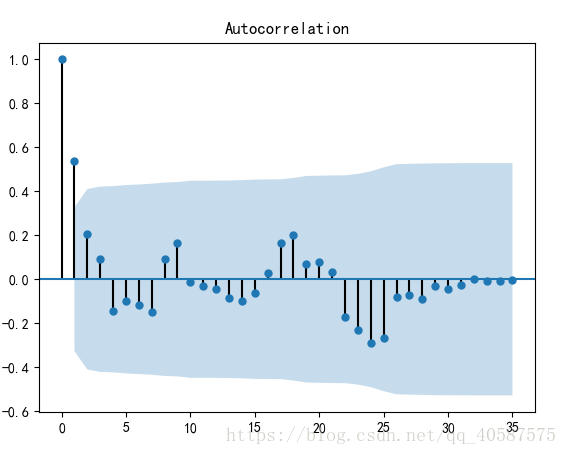
2.自相关图检验：平稳序列具有短期相关性，这个性质表明对平稳序列而言，通常只有近期的序列值得影响比较明显，间隔越远的过去值对现在的值得影响越小。而非平稳序列的自相关系数衰减的速度比较慢。

3.单位根检验：单位根检验是指检验序列中是否存在单位根，如果存在单位根，那就是非平稳时间序列。目前最常用的方法就是单位根检验。

原假设是非平稳序列过程，备择假设是平稳序列，趋势平稳过程

技术分享图片 ?

上述参考：百度文库

3.时间序列分析：

?平稳性：

?平稳性要求经由样本时间序列所得到的拟合曲线，在未来一段时间内仍然沿着现有的形态‘惯性’地延续下去。

?平稳性要求序列的均值和方差不发生明显的变化。

?弱平稳：期望和相关系数（依赖性）不变，未来某个时刻t 的值，Xt 要依赖于它过去的信息。

?差分法：时间序列在 T 与 T-1 时刻的差值（使用差分使其满足平稳性），一般差分1,2 阶就可以了。

?AR（自回归模型）：

?描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。

公式定义：技术分享图片 ?

技术分享图片 ?

自回归模型的限制：

1.自回归模型是使用自身的数据进行预测的

2.必须具有平稳性

3.必须具有相关性，如果相关性小于 0.5 ，则不宜使用

4.自回归模型只适用于预测与自身前期相关的预测。

?MA（移动平均模型）：

?移动平均模型关注的是自回归模型中的误差项的累加

?移动平均法能有效地消除预测中的随机波动。

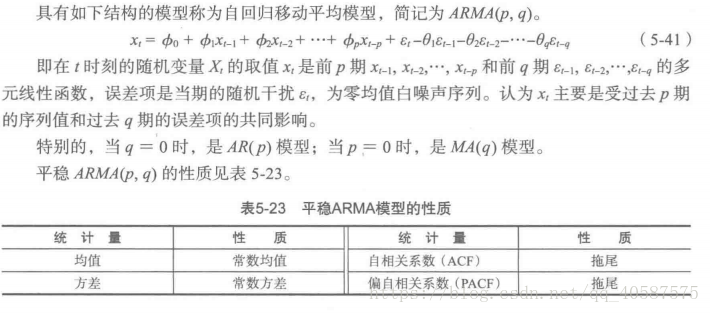
技术分享图片 ?

?ARMA（自回归平均模型）：

?自回归和移动平均的结合。

技术分享图片 ?

?ARIMA（p,d,q）差分自回归移动平均模型（Autoregressive Integrated Moving Average Model ,简称ARIMA）

?AR 是自回归， p 是自回归项， MA 是移动平均， q 为移动平均项， d 为时间序列称为平稳时所做的差分次数。

?原理：将非平稳时间序列转换成平稳时间序列，然后将因变量仅对它的滞后值（p阶）以及随机误差项的现值和滞后值进行回顾所建立的模型。

?ARIMA 建模流程：

?1.将序列平稳化（差分法确定 d）

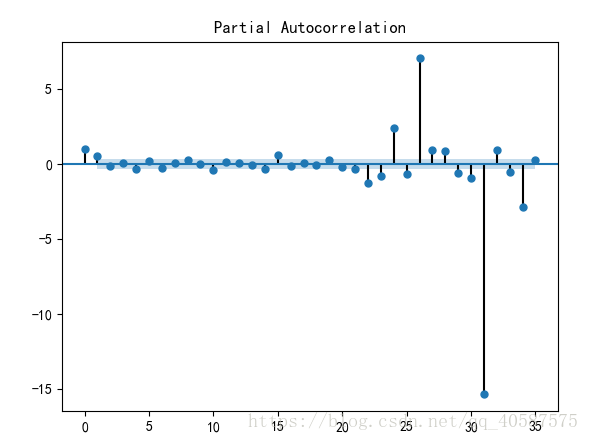
?2.p 和 q 阶数的确定（ACF 和 PACF 确定）

?3.建立模型 ARIMA (p , d , q )

技术分享图片 ?

使用ARIMA 模型对某餐厅的销售数据进行预测

#使用ARIMA 模型对非平稳时间序列进行建模操作
#差分运算具有强大的确定性的信息提取能力，许多非平稳的序列差分后显示出平稳序列的性质，这是称这个非平稳序列为差分平稳序列。
#对差分平稳序列可以还是要ARMA 模型进行拟合， ARIMA 模型的实质就是差分预算与 ARMA 模型的结合。

#coding=gbk
#使用ARIMA 模型对非平稳时间序列记性建模操作
#差分运算具有强大的确定性的信息提取能力， 许多非平稳的序列差分后显示出平稳序列的性质， 这是称这个非平稳序列为差分平稳序列。 
#对差分平稳序列可以还是要ARMA 模型进行拟合， ARIMA 模型的实质就是差分预算与 ARMA 模型的结合。 

#导入数据
import pandas as pd
filename = r‘D:datasetsarima_data.xls‘
data = pd.read_excel(filename, index_col = u‘日期‘)

#画出时序图
import matplotlib.pyplot as plt     
plt.rcParams[‘font.sans-serif‘] = [‘SimHei‘]    #定义使其正常显示中文字体黑体
plt.rcParams[‘axes.unicode_minus‘] = False      #用来正常显示表示负号
# data.plot()
# plt.show()

技术分享图片 ?

#画出自相关性图
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# plot_acf(data)
# plt.show()

#平稳性检测
from statsmodels.tsa.stattools import adfuller
print(‘原始序列的检验结果为：‘,adfuller(data[u‘销量‘]))
#原始序列的检验结果为： (1.8137710150945268, 0.9983759421514264, 10, 26, {‘1%‘: -3.7112123008648155,
#  ‘10%‘: -2.6300945562130176, ‘5%‘: -2.981246804733728}, 299.46989866024177)
#返回值依次为：adf, pvalue p值， usedlag, nobs, critical values临界值 , icbest, regresults, resstore 
#adf 分别大于3中不同检验水平的3个临界值，单位检测统计量对应的p 值显著大于 0.05 ， 说明序列可以判定为 非平稳序列

技术分享图片 ?

#对数据进行差分后得到 自相关图和 偏相关图
D_data = data.diff().dropna()
D_data.columns = [u‘销量差分‘]

D_data.plot()   #画出差分后的时序图
# plt.show()

plot_acf(D_data)    #画出自相关图
# plt.show()
plot_pacf(D_data)   #画出偏相关图
# plt.show()
print(u‘差分序列的ADF 检验结果为： ‘, adfuller(D_data[u‘销量差分‘]))   #平稳性检验
#差分序列的ADF 检验结果为：  (-3.1560562366723537, 0.022673435440048798, 0, 35, {‘1%‘: -3.6327426647230316, 
# ‘10%‘: -2.6130173469387756, ‘5%‘: -2.9485102040816327}, 287.5909090780334)
#一阶差分后的序列的时序图在均值附近比较平稳的波动， 自相关性有很强的短期相关性， 单位根检验 p值小于 0.05 ，所以说一阶差分后的序列是平稳序列

技术分享图片 ?

#对一阶差分后的序列做白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u‘差分序列的白噪声检验结果：‘,acorr_ljungbox(D_data, lags= 1)) #返回统计量和 p 值
# 差分序列的白噪声检验结果： (array([11.30402222]), array([0.00077339])) p值为第二项， 远小于 0.05

#对模型进行定阶
from statsmodels.tsa.arima_model import ARIMA 

pmax = int(len(D_data) / 10)    #一般阶数不超过 length /10
qmax = int(len(D_data) / 10)
bic_matrix = []
for p in range(pmax +1):
    temp= []
    for q in range(qmax+1):
        try:
            temp.append(ARIMA(data, (p, 1, q)).fit().bic)
        except:
            temp.append(None)
        bic_matrix.append(temp)

bic_matrix = pd.DataFrame(bic_matrix)   #将其转换成Dataframe 数据结构
p,q = bic_matrix.stack().idxmin()   #先使用stack 展平， 然后使用 idxmin 找出最小值的位置
print(u‘BIC 最小的p值 和 q 值：%s,%s‘ %(p,q))  #  BIC 最小的p值 和 q 值：0,1
#所以可以建立ARIMA 模型，ARIMA(0,1,1)
model = ARIMA(data, (p,1,q)).fit()
model.summary2()        #生成一份模型报告
model.forecast(5)   #为未来5天进行预测， 返回预测结果， 标准误差， 和置信区间