《信息学竞赛中构造题的常用解题方法》学习笔记

Posted 2023-05-01 Gemini7X の blog

orz jiangly

---

其实构造题还是非常的杂，除了一些套路，更多的做法还是考试的老老实实手玩。但很多人类智慧你没见过是想不出来的，所以这里总结一些做法。

抽屉原理

和为 \\(n\\) 的物品分成 \\(k\\) 组，最大的那组至少为 \\(\\lceil\\fracnk\\rceil\\)，最小的那组至多为 \\(\\lfloor\\fracnk\\rfloor\\)。

CF1450C2 Errich­Tac­Toe

给定一张 \\(n\\) 行 \\(n\\) 列的棋盘，每个格子可能是空的或包含一个标志，标志有 X 和 O 两种。如果有三个相同的标志排列在一行或一列上的三个连续的位置，则称这个棋盘是一个胜局，否则称其为平局。

设棋盘中标志的总数为 \\(k\\)，你需要用不超过 \\(\\lfloor\\frack3\\rfloor\\) 次操作把给定的局面变成平局。

把点根据 \\((i+j)%3\\) 分成三种，显然横着或竖着的三个是不同的种类。于是只要把所有 \\(0\\) 种的 O 换成 X，以及所有 \\(1\\) 中的 X 换成 O。以及类似的剩下两种操作中的一种即可。三种操作中最小的那一种一定 \\(\\le \\lfloor\\frack3\\rfloor\\)。

code

2020 ICPC Asia Shanghai Reginal Contest B Mine Sweeper II

扫雷地图是一张 \\(n\\) 行 \\(m\\) 列的网格，其中每个格子是地雷或空地。每个空地会显示一个数字代表与它相邻的雷的数量（两个格子相邻当且仅当它们共用一个顶点或一条边，不在边界上的格子与恰好 \\(8\\) 个格子相邻）。

在一次操作中，你可以将一个地雷改成空地，或将空地改成地雷。

给定两张扫雷地图 A，B，你需要对 B 进行不超过 \\(\\lfloor\\fracnm2\\rfloor\\) 次操作，使得 A 所有空地上的数字之和等于 B 所有空地上的数字之和。

本题的关键在于发现，如果将雷和空地全部取反，数值不变。于是我们就用两种简单的变法，把 B 变成 A 一样以及把 B 变成 A 取反。两者显然不交且和等于 \\(nm\\)，所以较小的那种一定不超过 \\(\\lfloor\\fracnm2\\rfloor\\)。

图遍历

一些构造题是在一个图上或者需要你建出一个图论模型。一般这种题都要简化问题，比如找一个环（欧拉路径，哈密顿路径）或一棵树（dfs、bfs 树）。或者根据 2-sat 或者差分约束建图（这不在今天的讨论范围内）。

dfs 树的性质是，不存在前向边和横叉边。

CF1364D Ehab’s Last Corollary

给定一张 \\(n\\) 个点 \\(m\\) 条边的无向连通图，以及一个整数 \\(k\\)，你需要

• 找到一个恰好 \\(\\lceil\\frack2\\rceil\\) 个点的独立集，
• 或者找到一个长度不超过 \\(k\\) 的简单环。

找一棵dfs树，如果这个图有环且最小环长超过 \\(k\\)，那么在这个环上隔一个点选一个即可。找环用返祖边即可。如果没有环给树黑白染色，取较大的一边作为独立集即可。

code

IOI2019 景点划分

给定一张 \\(n\\) 个点 \\(m\\) 条边的无向连通图，以及三个整数 \\(a,b,c\\)，满足 \\(a+b+c=n\\)。你需要将 \\(n\\) 个顶点分成三个集合 \\(A,B,C\\)，大小分别为 \\(a,b,c\\)，使得其中至少两个集合是连通的(集合中的任意两个点能只经过该集合内的点互相到达)。有可能无解。

不妨设 \\(a\\le b\\le c\\)，那么显然我们让 \\(A,B\\) 连通就好。先考虑树的情况，考虑把重心拿出来当根，如果重心存在一个子树不小于 \\(a\\) 选它即可，然后剩下的部分一定 \\(\\ge \\fracn2\\) 所以给 B 是一定够的。如果不存在显然就无解了。

如果是一个图，先找出一个dfs生成树以及其重心，假设是 \\(u\\)。如果满足刚刚的有解可以直接仿照树的情况构造。

否则的话由于dfs树不存在横叉边，所以只用考虑跳到 \\(u\\) 父亲那个子树的边。于是在那个子树和剩下的子树里选一个相通的点集，这个点集在 \\([a,2a]\\) 之内。如果不存在就无解，否则剩下的点一定大于等于 \\(b\\)，那么也可以选出一个 B 来。

code

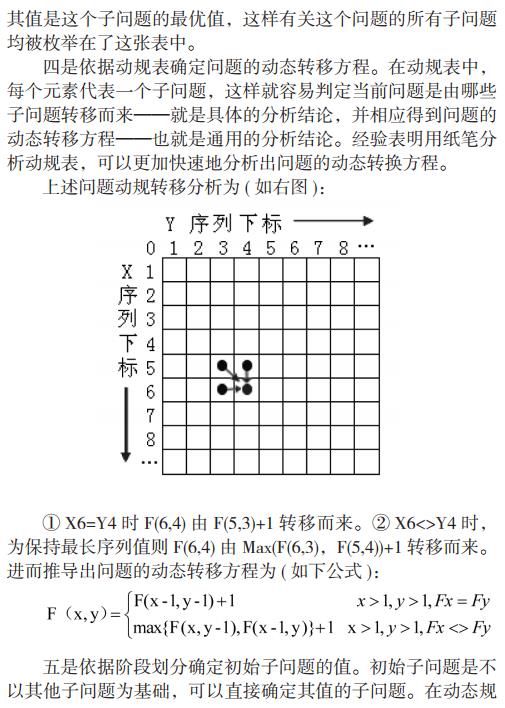
信息学信息学竞赛中动态规划类程序设计的算法分析

「中学网络教育头部品牌 微信ID：youyike100」

高考动态、学习方法、励志成长、名师对话

更多名师、金课合作

请联系我们

优易课汇聚了一支国内教育名家、高考命题专家和阅卷名师、为考试把脉的国家级名师科研培训队伍，结合国内顶级的优质教育资源，为广大高三毕业班的老师、同学输出精品课程，

不论您的学校位于哪里，段姜华、王大绩、周沛耕、范存智、梁侠等国家级名师团队都将和您一起，为您的学生们提供语、数、外、政、史、地、物、化、生精品课程，紧跟高考热点，涵盖高考各个阶段的全部课程，帮助同学们根据自己的时间和进度独立学习，个性化提升成绩，帮助同学们快速提升学习效能，冲刺高考。

借助于优易课的名师金课，全国各地的高考班老师们都可以随时组织“线上线下混合式双师课堂”，根据本班同学的共性需求和个性化需求，针对性地开展考前复习、练习，优易课还提供了数以千万计的题库，并由参加了历年高考评卷、阅卷工作的名师为同学们加以讲解。