对时间序列数据作出指数平滑预测后，如何用excel计算数据的均方误差（MSE）？

Posted 2023-05-01

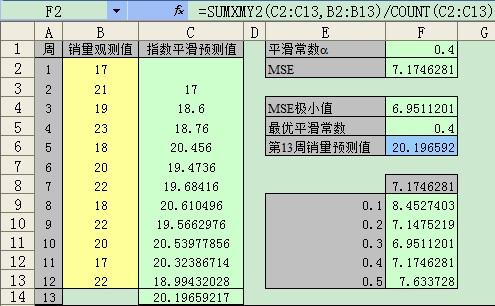
=SUMXMY2(C2:C13,B2:B13)/COUNT(C2:C13)

=SUMXMY2(不包括预测年的全部预测值,全部观测值)/COUNT（预测值的个数)

举例见图片：） 图片里F5的数字应该是0.3，我当时用了控件所以。。。

不懂再问我哦~今天我有空

参考技术A 我想要用excel进行对数据的分析以及预测，例如是对销售收入的数据，应该怎么工具－加载宏 把分析工具库前面打勾然后 工具－数据分析－指数平滑输入区域

Python 时间序列建模：用指数平滑法预测股价走势

指数平滑方法适用于非平稳数据（即具有趋势和/或季节性的数据），其工作方式类似于指数移动平均线。预测是过去观察的加权平均值。这些模型更加强调最近的观察结果，因为权重随时间呈指数级变小。平滑方法很受欢迎，因为它们速度快（不需要大量计算）并且在预测方面相对可靠。（扫描本文最下方二维码获取全部完整源码和Jupyter Notebook 文件打包下载。）

简单指数平滑法：

Simple Exponential Smoothing，最基本的模型称为简单指数平滑（SES）。这类模型最适用于所考虑的时间序列不表现出任何趋势或季节性的情况。它们也适用于只有几个数据点的系列。

该模型通过平滑参数 α 进行参数化，其值介于 0 和 1 之间。值越高，对最近观察的权重就越大。当 α = 0 时，对未来的预测等于历史数据（模型拟合的数据）的平均值。当 α = 1 时，所有预测值都与训练数据中的最后一个观察值相同。

简单指数平滑的预测函数是平坦的，即所有的预测，无论时间跨度如何，都等于同一个值——最后一个级别的分量。这就是为什么这种方法只适用于既没有趋势也没有季节性的序列。

二次指数平滑法：

Holt 的模型是简单指数平滑（SES）的扩展，它通过将趋势分量添加到模型规范中来说明序列中的趋势。当数据存在趋势但没有季节性时，应使用此模型。

Holt 模型的一个问题是趋势在未来是恒定的，这意味着它会无限增加/减少。这就是模型的扩展通过添加阻尼参数 φ 来抑制趋势的原因。它使趋势在未来收敛到一个恒定值，从而有效地将其拉平。Hyndman 和 Athanasopoulos (2018) 指出 φ 很少小于 0.8，因为阻尼对较小的 φ 值具有非常强的影响。

最佳做法是限制 φ 的值，使其介于 0.8 和 0.98 之间，因为对于 φ = 1，阻尼模型等效于没有阻尼的模型。

在本文中，我们将向您展示如何将平滑方法应用于 Google 的每月股票价格（具有趋势且没有明显季节性的非平稳数据）。我们将模型与 2010-2017 年的价格进行拟合，并对 2018 年进行预测。

准备

在下文中，我们将在相同的图上绘制多条线，每条线代表不同模型的类型。这就是为什么我们要确保这些线条清晰可辨，尤其是黑白线条。出于这个原因，我们将为绘图使用不同的调色板，即cubehelix：

plt.set_cmap('cubehelix')
sns.set_palette('cubehelix')


COLORS = [plt.cm.cubehelix(x) for x in [0.1, 0.3, 0.5, 0.7]]

步骤

执行以下步骤以使用指数平滑方法来创建对 Google 股票价格的预测。

1、导入第三方库：

import pandas as pd
import numpy as np
import yfinance as yf
from datetime import date
from statsmodels.tsa.holtwinters import (ExponentialSmoothing, 
                                         SimpleExpSmoothing, 
                                         Holt)

2、下载调整后的谷歌股价数据：

df = yf.download('GOOG',
                 start='2010-01-01',
                 end='2018-12-31',
                 adjusted=True,
                 progress=False)


print(f'Downloaded {df.shape[0]} rows of data.')

3、汇总到每月频率：

goog = df.resample('M') \\
         .last() \\
         .rename(columns={'Adj Close': 'adj_close'}) \\
         .adj_close

4、创建训练/测试集

train_indices = goog.index.year < 2018
goog_train = goog[train_indices]
goog_test = goog[~train_indices]


test_length = len(goog_test)

5、绘制价格走势图

goog.plot(title="Google's Stock Price")


plt.tight_layout()
#plt.savefig('images/ch3_im14.png')
plt.show()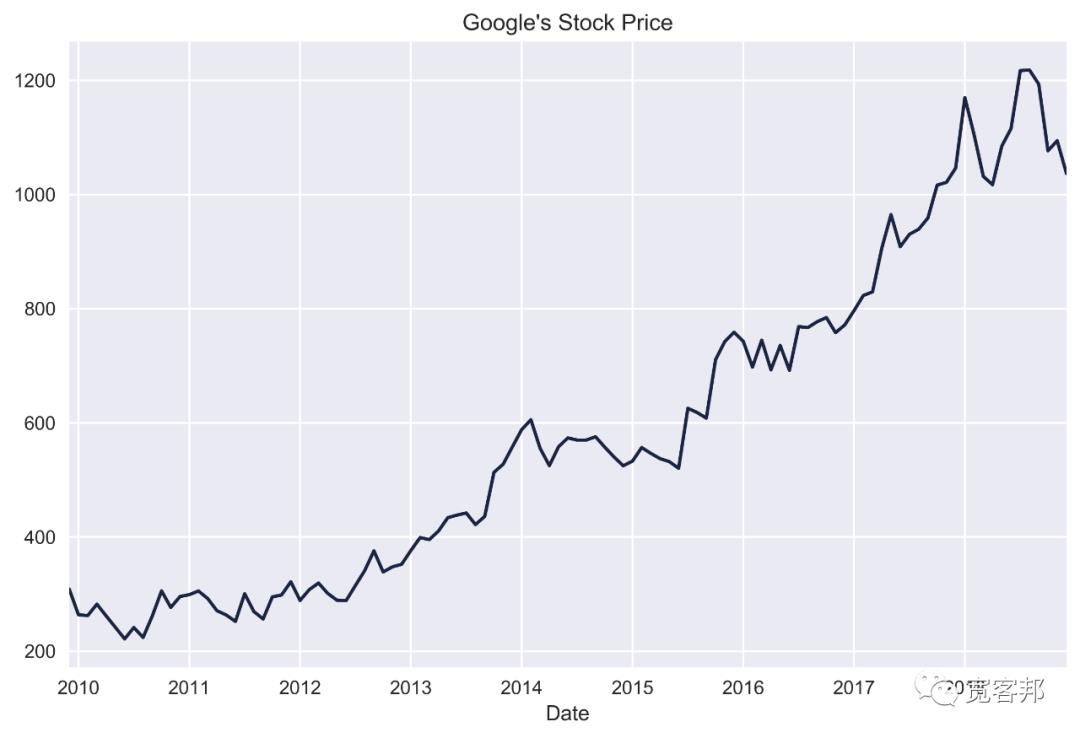

6、拟合三个简单指数平滑（SES）模型并为它们创建预测：

ses_1 = SimpleExpSmoothing(goog_train).fit(smoothing_level=0.2)
ses_forecast_1 = ses_1.forecast(test_length)


ses_2 = SimpleExpSmoothing(goog_train).fit(smoothing_level=0.5)
ses_forecast_2 = ses_2.forecast(test_length)


ses_3 = SimpleExpSmoothing(goog_train).fit()
alpha = ses_3.model.params['smoothing_level']
ses_forecast_3 = ses_3.forecast(test_length)

7、绘制原始价格和模型的结果：

goog.plot(color=COLORS[0], 
          title='Simple Exponential Smoothing',
          label='Actual',
          legend=True)


ses_forecast_1.plot(color=COLORS[1], legend=True, 
                    label=r'$\\alpha=0.2$')
ses_1.fittedvalues.plot(color=COLORS[1])


ses_forecast_2.plot(color=COLORS[2], legend=True, 
                    label=r'$\\alpha=0.5$')
ses_2.fittedvalues.plot(color=COLORS[2])


ses_forecast_3.plot(color=COLORS[3], legend=True, 
                    label=r'$\\alpha={0:.4f}$'.format(alpha))
ses_3.fittedvalues.plot(color=COLORS[3])


plt.tight_layout()
#plt.savefig('images/ch3_im15.png')
plt.show()

执行代码会生成下图：

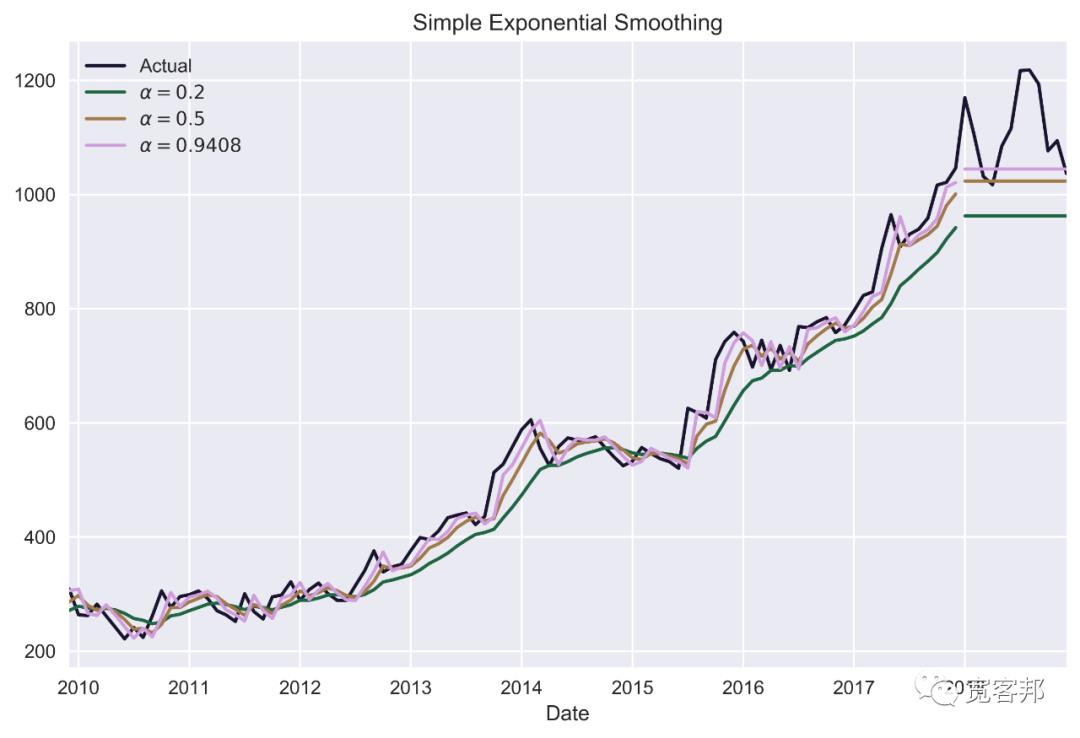
在前面的图中，我们可以看到我们在本文的介绍中描述的 SES 的特征——预测是一条平坦的线。我们还可以看到 statsmodels 优化程序选择的最优值接近 1。此外，第三个模型的拟合线实际上是观察到的价格向右移动的线。

8、拟合 Holt 平滑模型的三个变体并创建预测：

# Holt's model with linear trend
hs_1 = Holt(goog_train).fit()
hs_forecast_1 = hs_1.forecast(test_length)


# Holt's model with exponential trend
hs_2 = Holt(goog_train, exponential=True).fit()
# equivalent to ExponentialSmoothing(goog_train, trend='mul').fit()
hs_forecast_2 = hs_2.forecast(test_length)


# Holt's model with exponential trend and damping
hs_3 = Holt(goog_train, exponential=False, 
            damped=True).fit(damping_slope=0.99)
hs_forecast_3 = hs_3.forecast(test_length)

9、绘制原始价格和模型的结果：

goog.plot(color=COLORS[0],
          title="Holt's Smoothing models",
          label='Actual',
          legend=True)


hs_1.fittedvalues.plot(color=COLORS[1])
hs_forecast_1.plot(color=COLORS[1], legend=True, 
                   label='Linear trend')


hs_2.fittedvalues.plot(color=COLORS[2])
hs_forecast_2.plot(color=COLORS[2], legend=True, 
                   label='Exponential trend')


hs_3.fittedvalues.plot(color=COLORS[3])
hs_forecast_3.plot(color=COLORS[3], legend=True, 
                   label='Exponential trend (damped)')


plt.tight_layout()
#plt.savefig('images/ch3_im16.png')
plt.show()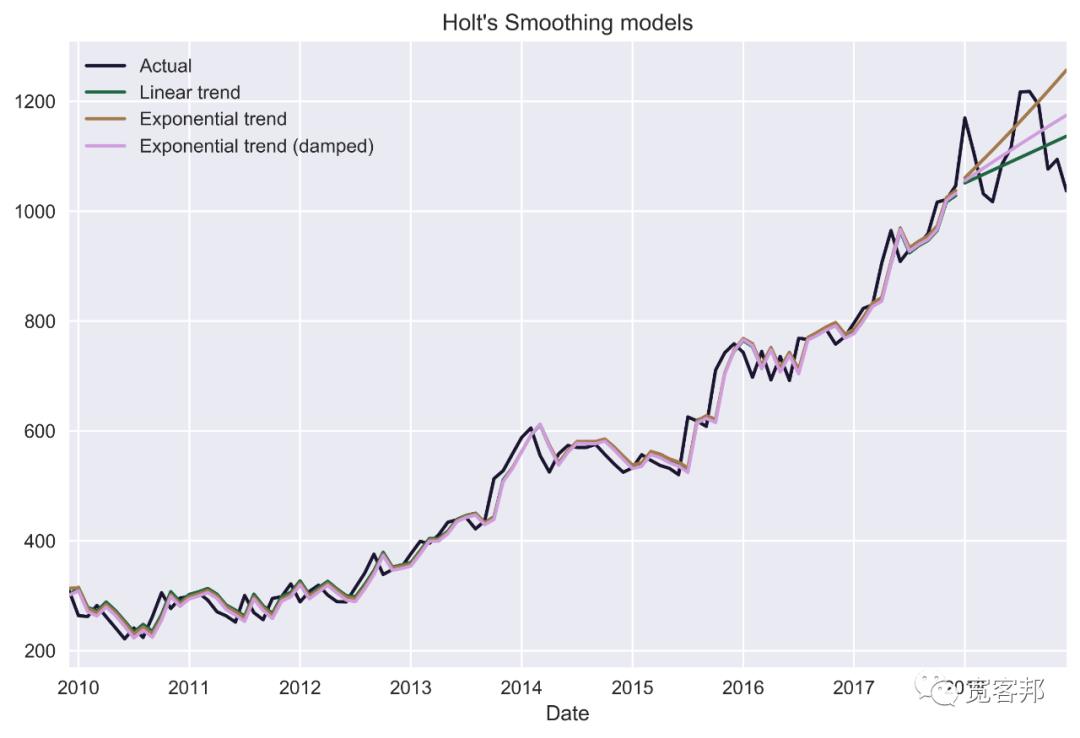

工作原理

在第 2 步到第 5 步中，我们下载了 2010-2018 年 Google 的股票价格，将这些值重新采样到每月频率，将数据拆分为训练（2010-2017）和测试（2018）集，并绘制了系列图。

在第 6 步中，我们使用 SimpleExpSmoothing 类及其拟合方法拟合了三个不同的 SES 模型。对于拟合，我们只使用了训练数据。我们可以手动选择平滑参数 (smoothing_level) 的值，但是，最佳实践是让 statsmodels 优化它以获得最佳拟合。这种优化是通过最小化残差平方和（误差）来完成的。我们使用预测方法创建了预测，该方法需要我们要预测的周期数（等于测试集的长度）。在第 7 步中，我们将结果可视化并将其与实际股票价格进行比较。我们使用拟合模型的拟合值方法提取模型的拟合值。

在第 8 步中，我们使用了 Holt 类（它是更加 通用的ExponentialSmoothing 类）以适合 Holt 的线性趋势模型。默认情况下，模型中的趋势是线性的，但我们可以通过指定exponential=True 并使用damped=True添加阻尼来使其呈指数增长。与 SES 的情况一样，使用不带参数的 fit 方法会导致运行优化例程以确定参数的最佳值。我们可以通过运行fitted_model.params来访问它。在示例中，我们手动将阻尼参数的值指定为 0.99，因为优化器选择 1 作为最佳值，这在图上是无法区分的。在第 9 步中，我们将结果可视化。

三次指数平滑法（holt-winters）

Holt 的方法有一个扩展，称为 Holt-Winter 季节性平滑法。它考虑了时间序列中的季节性。此模型没有单独的类，但我们可以通过添加seasonal 和seasonal_periods 参数来调整ExponentialSmoothing 类。

无需过多赘述，此方法最适合具有趋势和季节性的数据。该模型有两种变体，它们具有加法或乘法季节性。在前一种中，季节变化在整个时间序列中或多或少是恒定的。在后者中，变化与时间的流逝成比例地变化。

我们首先拟合模型：

SEASONAL_PERIODS = 12


# Holt-Winter's model with exponential trend
hw_1 = ExponentialSmoothing(goog_train, 
                            trend='mul', 
                            seasonal='add', 
                            seasonal_periods=SEASONAL_PERIODS).fit()
hw_forecast_1 = hw_1.forecast(test_length)


# Holt-Winter's model with exponential trend and damping
hw_2 = ExponentialSmoothing(goog_train, 
                            trend='mul', 
                            seasonal='add', 
                            seasonal_periods=SEASONAL_PERIODS, 
                            damped=True).fit()
hw_forecast_2 = hw_2.forecast(test_length)

然后我们绘制结果：

goog.plot(color=COLORS[0],
          title="Holt-Winter's Seasonal Smoothing",
          label='Actual',
          legend=True)


hw_1.fittedvalues.plot(color=COLORS[1])
hw_forecast_1.plot(color=COLORS[1], legend=True, 
                   label='Seasonal Smoothing')


phi = hw_2.model.params['damping_slope']
plot_label = f'Seasonal Smoothing (damped with $\\phi={phi:.4f}$)'


hw_2.fittedvalues.plot(color=COLORS[2])
hw_forecast_2.plot(color=COLORS[2], legend=True, 
                   label=plot_label)


plt.tight_layout()
#plt.savefig('images/ch3_im17.png')
plt.show()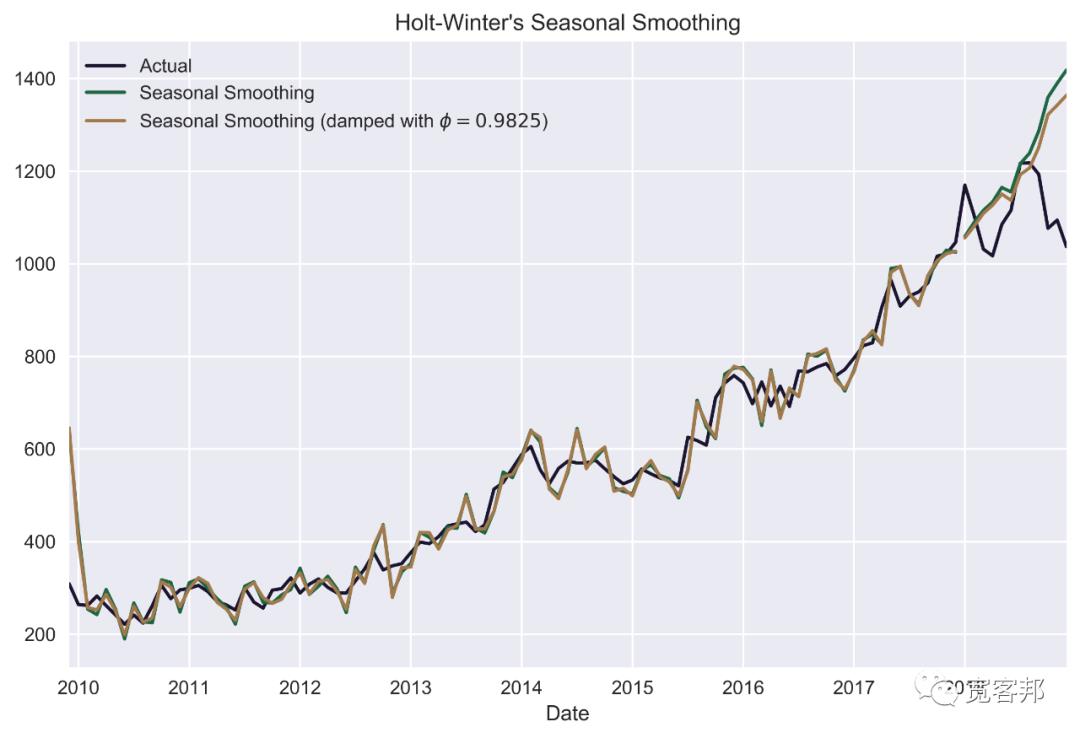

从绘制的预测图中，我们可以看到，与 SES 和 Holt 的线性趋势模型相比，该模型更加灵活。序列开始时的极端拟合值是由于没有足够的观察值可供回溯（我们在处理月度数据时选择了seasonal_periods=12）。

E N D

扫描本文最下方二维码获取全部完整源码和Jupyter Notebook 文件打包下载。

↓↓长按扫码获取完整源码↓↓