莫队
Posted 邪童的博客
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了莫队相关的知识,希望对你有一定的参考价值。
莫队是一类离线区间询问问题, 经常应用于需要维护的信息无法合并时(如线段树等)
其核心思想是: 维护两个指针
l,r. 在已知[l,r]这段区间的信息的前提下, 两个指针分别移动到l\',r\'的过程中, 实时地维护答案, 从而算出区间[l,r]的信息
莫队之基础莫队
莫队是一类离线区间询问问题, 核心是对大量的询问进行处理, 每个询问一般都有一个区间
[l,r], 我们对询问进行分块维护两个指针
l,r, 在已知[l,r]这段区间的信息的前提下, 两个指针分别移动到l\',r\'的过程中, 实时地维护答案, 从而算出区间[l,r]的信息
对询问进行分块
① 按照
[l,r],l递增进行排序, 分成 \\(\\sqrtn\\) 块② 每一块内部按照
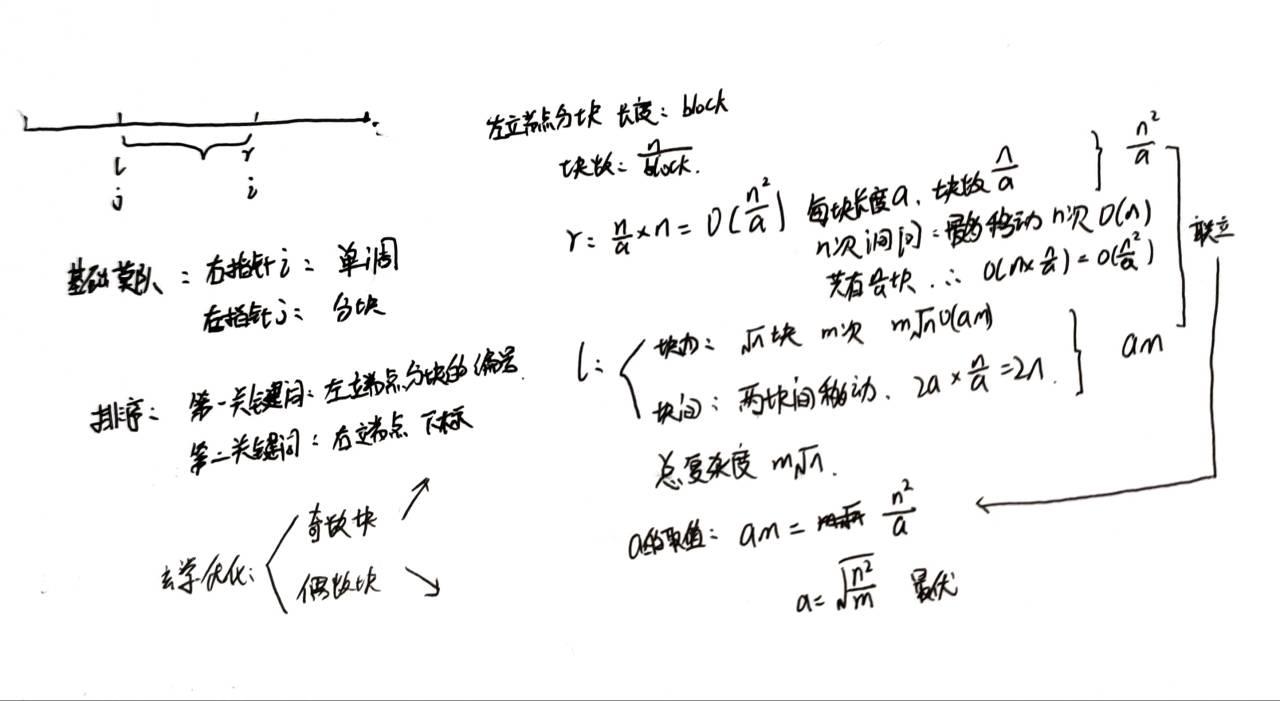
r排序优化: 分块长度
len= \\(\\sqrt\\dfracn^2m\\) , (n为数组长度,m为询问个数)\\(\\quad\\) \\(\\quad\\) 奇数块内
r从小到大排序, 偶数块内r从大到小排序
//基础莫队算法模板
int n,m,len; //n为数组长度,m为询问个数,len为分块长度
int w[N],ans[M],cnt[S]; //w[]记录数组,ans[]记录每个询问答案,cnt[]数组实时维护每个元素出现的次数
struct Query
int id,l,r;
q[M]; //离线记录询问
int get (int l) //按左端点分块
return l/len;
bool cmp (const Query&a,const Query &b) //按询问排序
int i=get(a.l),j=get(b.l);
if(i!=l)return i<j; //第一关键字:左端点l分块从小到大排序
else return a.r<b.r; //第二关键字:同一块内,按右端点r排序
void add (int x,int &res)
if(!cnt[x])res++;
cnt[x]++;
void del (int x,int &res)
cnt[x]--;
if(!cnt[x])res--;
int main()
cin>>n;
for(int i=1;i<=n;i++)cin>>w[i];
cin>>m;
len=max(1,(int)sqrt((double)n*n/m));
for(int i=0;i<m;i++)
int l,r;
cin>>l>>r;
q[i]=i,l,r;
sort(q,q+m,cmp);
for(int k=0,i=0,j=1,res=0;k<m;k++) //i是向r靠齐的指针,j是向l靠齐的指针
int id=q[k].id,l=q[k].l,r=q[k].r;
while(i<r)add(w[++i],res);
while(i>r)del(w[i--],res);
while(j<l)del(w[j++],res);
while(j>l)add(w[--j],res);
ans[id]=res;
for(int i=0;i<m;i++)cout<<ans[i]<<\'\\n\';
return 0;
莫队之待修改的莫队
在离线莫队里加入时间戳
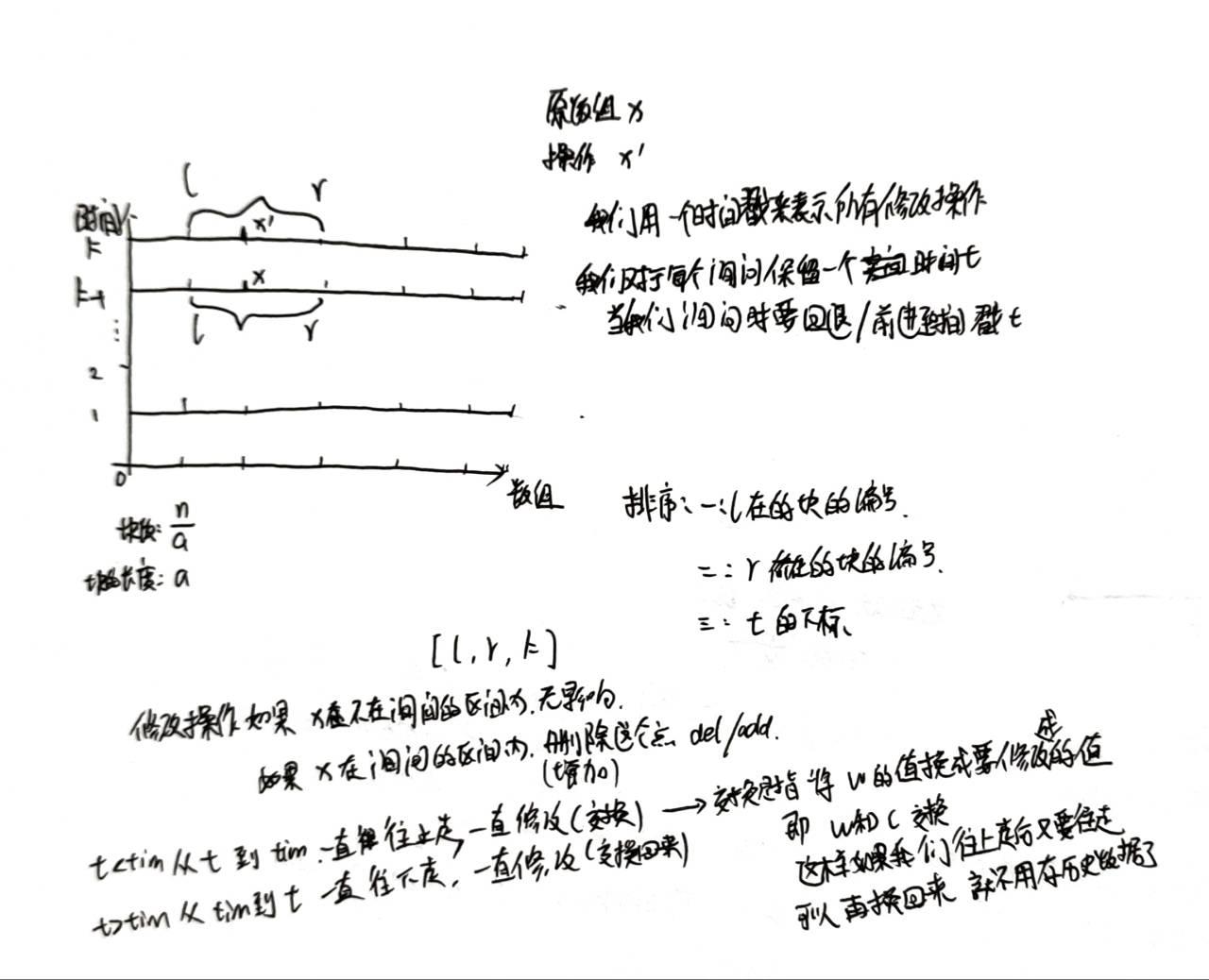
(l,r,t)对于操作来说, 我们把修改和询问分开
对于询问: 左端点所在块为第一关键字, 右端点所在块为第二关键字, 时间为第三关键字进行排序
与普通莫队相似, 只需要多维护一个修改的操作: 假设两个询问的时间分别为
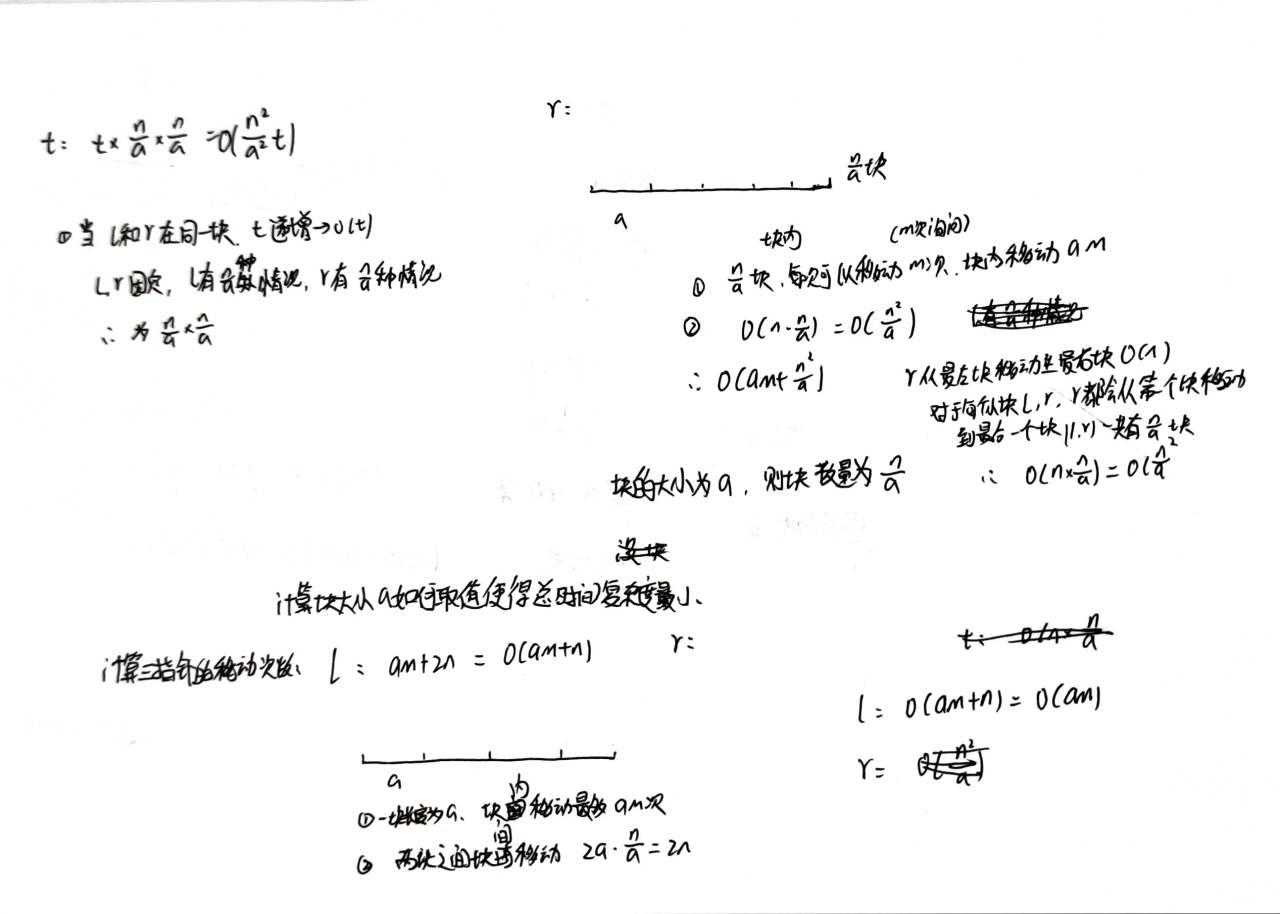
t1,t2, 只需要把[t1,t2]这段时间内的修改操作执行一遍(时光正流或倒流)优化:
len= \\(\\sqrt[3]nt + 1\\) , (n为元素个数,t为时间/操作次数)
//带修莫队算法模板
int n,m,mq,mc,len; //n为元素个数,mq为询问次数,mc为操作次数
int w[N],cnt[S],ans[M];
struct Query //记录询问
int id,l,r,t;
q[M];
struct Modify //记录操作
int p,c;
c[M];
int get (int x)
return x/len;
bool cmp (const Query&a,const Query&b)
int al=get(a.l),ar=get(a.r);
int bl=get(b.l),br=get(b.r);
if(al!=bl)return al<bl;
if(ar!=br)return ar<br;
return a.t<b.t;
void add (int x,int &res)
if(!cnt[x])res++;
cnt[x]++;
void del (int x,int &res)
cnt[x]--;
if(!cnt[x])res--;
int main()
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>w[i];
for(int i=0;i<m;i++)
char op[2];
int a,b;
cin>>op>>a>>b;
if(*op==\'Q\')mq++,q[mq]=mq,a,b,mc; //记录询问
else c[++mc]=a,b; //记录操作
len=cbrt((double)n*max(1,mc))+1;
sort(q+1,q+1+mq,cmp);
for(int k=1,i=0,j=1,res=0,t=0;k<=mq;k++)
int id=q[k].id,l=q[k].l,r=q[k].r,tm=q[k].t;
while(i<r)add(w[++i],res);
while(i>r)del(w[i--],res);
while(j<l)del(w[j++],res);
while(j>l)add(w[--j],res);
while(t<tm)
t++;
if(c[t].p>=l&&c[t].p<=r)
del(w[c[t].p],res);
add(c[t].c,res);
swap(w[c[t].p],c[t].c);
while(t>tm)
if(c[t].p>=l&&c[t].p<=r)
del(w[c[t].p],res);
add(c[t].c,res);
swap(w[c[t].p],c[t].c);
t--;
ans[idx]=res;
for(int i=1;i<=mq;i++)cout<<ans[i]<<\' \';
return 0;
莫队之回滚莫队
回滚莫队用于维护一段区间内的
max或min处理一段区间分为两部分:
① 对于左端点
l和右端点r在同一段内的区间, 暴力处理② 对于左端点
l和右端点r不在同一段内的区间, 分别处理[l,right]和[right+1,r]以左端点所在的块升序为第一关键字, 以右端点升序为第二关键字
//回滚莫队算法模板
int n,m,len;
int w[N],cnt[N];
long long ans[N];
vector<int> nums;
struct Query
int id,l,r;
q[N];
int get (int x)
return x/len;
bool cmp (const Query&a,const Query&b)
int i=get(a.l),j=get(b.l);
if(i!j) return i<j;
else a.r<b.r;
void add (int x,long long &res) //回滚莫队只有增加操作,没有删减操作
cnt[x]++;
res=max(res,(long long)cnt[x]*nums[x]);
int main()
cin>>n>>m;
len=sqrt(n);
for(int i=1;i<=n;i++)cin>>w[i],nums.push_back(w[i]);
sort(nums.begin(),nums.end()); //离散化
nums.erase(unique(nums.begin(),nums.end()),nums.end());
for(int i=1;i<=n;i++)
w[i]=lower_bound(nums.begin(),nums.end(),w[i])-nums.begin();
//w[i]存储原数在离散化数组nums中的下标
for(int i=0;i<m;i++)
int l,r;
cin>>l>>r;
q[i]=i,l,r;
sort(q,q+m,cmp);
for(int x=0;x<m;)
int y=x; //处理左端点l在同一段内的所有询问[x,y)
while(y<m&&get(q[y].l)==get(q[x].l))y++;
int right=(get(q[x].l)+1)*len-1; //左端点l所在段终点为right
//暴力求右端点r在块内的询问
while(x<y&&q[x].r<=right)
long long res=0;
int id=q[x].id,l=q[x].l,r=q[x].r;
for(int k=l;k<=r;k++)add(w[k],res);
ans[id]=res;
for(int k=l;k<=r;k++)cnt[w[k]]--; //复原
x++;
//求右端点r在块外的询问
long long res=0;
int i=right,j=right+1; //i是右指针,j是左指针
while(x<y)
int id=q[x].id,l=q[x].l,r=q[x].r;
while(i<r)add(w[++i],res);
long long backup=res; //备份[right+1,r]的res值
while(j>l)add(w[--j],res);
ans[id]=res;
while(j<right+1)cnt[w[j++]]--; //复原
res=backup;
x++;
memset(cnt,0,sizeof cnt);
for(int i=0;i<m;i++)cout<<ans[i]<<\' \';
return 0;
算法笔记莫队算法(基础莫队,带修莫队,回滚莫队,树上莫队,二次离线莫队)
整理的算法模板合集: ACM模板
目录
来这里学习莫队以及神奇的证明:莫队算法 --算法竞赛专题解析(26)
我们首先考虑双指针的暴力法,发现很容易就会被卡成 O ( n m ) O(nm) O(nm),这时候我们的莫队出现了,莫队说,我可以像变魔术一样,把 O ( n m ) O(nm) O(nm)的算法通过一个神奇的排序方式,使得我们最坏的情况下,时间复杂度也会非常优秀: O ( n n ) O(n\\sqrtn) O(nn)。
莫队算法是一个离线的算法,我们先将所有的询问全部存下来,然后排序。我们的每一个询问都是一个左右区间, ( l , r ) (l ,r) (l,r)
我们的排序方法为双关键字排序,我们将每个询问的左端点
l
l
l 分块。
第一关键字为左端点分块的编号从小到大,第二关键字为右端点的下标从小到大。
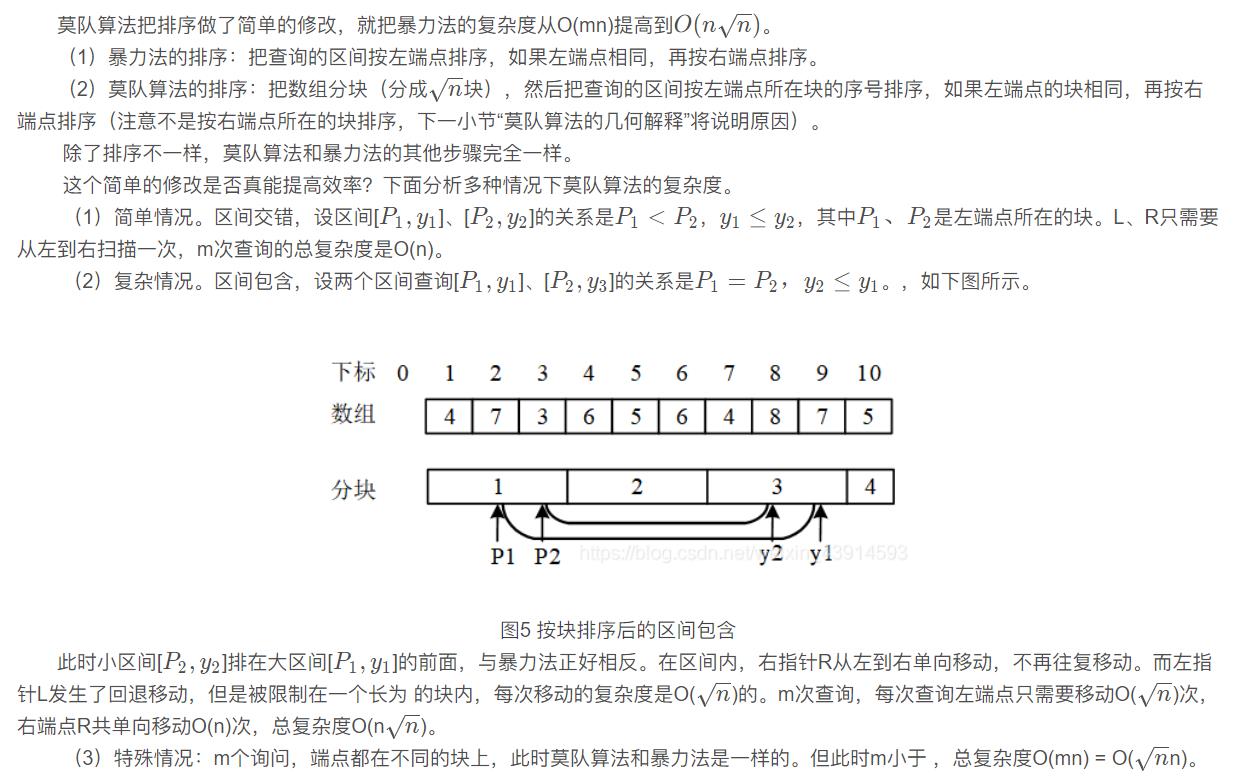
编码时,还可以对排序做一个小优化:奇偶性排序,让奇数块和偶数块的排序相反。例如左端点L都在奇数块,则对R从大到小排序;若L在偶数块,则对R从小到大排序(反过来也可以:奇数块从小到大,偶数块从大到小)。
1. 基础莫队
AcWing 2492. HH的项链

#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>
using namespace std;
const int N = 50007, M = 200007, S = 1000007;
int n, m;
int w[N];
int block;
int cnt[S];
int ans[M];
struct Query
int id, l, r;
q[M];
int get_block(int x)
return x / block;//这里是从0开始
bool cmp(const Query& x, const Query& y)
int a = get_block(x.l);
int b = get_block(y.l);
if(a != b)return a < b;
return x.r < y.r;
void add(int x, int &res)
if(cnt[x] == 0)res ++ ;
cnt[x] ++ ;
void del(int x, int &res)
cnt[x] -- ;
if(cnt[x] == 0)res -- ;
int main()
scanf("%d", &n);
for(int i = 1; i <= n; ++ i) scanf("%d", &w[i]);
scanf("%d", &m);
block = sqrt((double)n * n / m);//1488 ms
//block = sqrt(n); //1700 ms
for(int i = 0; i < m; ++ i)
int l, r;
scanf("%d%d", &l, &r);
q[i] = i, l, r;
sort(q, q + m, cmp);
for(int k = 0, i = 0, j = 1, res = 0; k < m; ++ k)
int id = q[k].id, l = q[k].l, r = q[k].r;
while(i < r)add(w[ ++ i], res);
while(i > r)del(w[i -- ], res);
while(j < l)del(w[j ++ ], res);
while(j > l)add(w[ -- j], res);//注意这里的细节,自己模拟一遍
ans[id] = res;
for(int i = 0; i < m; ++ i)
printf("%d\\n", ans[i]);
return 0;
玄学优化版,成功卡过了洛谷上的这道题
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>
using namespace std;
const int N = 1000007, M = 1000007, S = 1000007;
int n, m;
int w[N];
int block;
int cnt[S];
int ans[M];
inline int read()
int x = 0, f = 1;
char ch = getchar();
while(ch > '9' || ch < '0')if(ch == '-')f = -1;ch = getchar();
while(ch >= '0' && ch <= '9')x = x * 10 + ch - '0';ch = getchar();
return x * f;
inline void write(int res)
if(res<0)
putchar('-');
res=-res;
if(res>9)
write(res/10);
putchar(res%10+'0');
struct Query
int id, l, r;
q[M];
inline int get_block(int x)
return x / 2000;//这里是从0开始
bool cmp(const Query& x, const Query& y)
int a = get_block(x.l);
int b = get_block(y.l);
//int a = x.l / block, b = y.l / block;
if(a != b)return a < b;
if(a & 1)return x.r < y.r;
return x.r > y.r;
inline void add(int x, int &res)
if(cnt[x] == 0)res ++ ;
cnt[x] ++ ;
inline void del(int x, int &res)
cnt[x] -- ;
if(cnt[x] == 0)res -- ;
int main()
n = read();
for(register int i = 1; i <= n; ++ i) w[i] = read();
m = read();
block = sqrt((double)n * n / m);//1488 ms
//block = sqrt(n); //1700 ms
//block = 2000;
for(register int i = 0; i < m; ++ i)
int l = read(), r = read();
q[i] = i, l, r;
sort(q, q + m, cmp);
for(register int k = 0, i = 0, j = 1, res = 0; k < m; ++ k)
int id = q[k].id, l = q[k].l, r = q[k].r;
while(i < r)add(w[ ++ i], res);
while(i > r)del(w[i -- ], res);
while(j < l)del(w[j ++ ], res);
while(j > l)add(w[ -- j], res);//注意这里的细节,自己模拟一遍
/*
while(i < r)res += ++ cnt[w[ ++ i]] == 1;
while(i > r)res -= -- cnt[w[i -- ]] == 0;
while(j < l)res -= -- cnt[w[j ++ ]] == 0;
while(j > l)res += ++ cnt[w[ -- j]] == 1;
*/
ans[id] = res;
for(register int i = 0; i < m; ++ i)
write(ans[i]), puts("");
return 0;
2. 带修莫队
AcWing 2521. 数颜色


我发现直接把块的大小开成一个常数跑的最快…
//#pragma GCC optimize(2)
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <iostream>
#include <cmath>
using namespace std;
const int N = 1000007, M = 1000007, S = 1000007;
inline int read()
int x = 0, f = 1;
char ch = getchar();
while(ch > '9' || ch < '0')if(ch == '-')f = -1;ch = getchar();
while(ch >= '0' && ch <= '9')x = x * 10 + ch - '0';ch = getchar();
return x * f;
inline void write(int res)
if(res<0)
putchar('-');
res=-res;
if(res>9)
write(res/10);
putchar(res%10+'0');
int n, m;
int block = 2589;//n ^ (2 / 3)
int w[N];
int cnt[S];
int ans[N];
int bi[N];
struct Query
int id, l, r, t;
q[M];
struct Modify
int pos, col, lst;
c[M];
bool cmp(const Query &a, const Query &b)
int al = bi[a.l], ar = bi[a.r];
int bl = bi[b.l], br = bi[b.r];
if(al != bl)return a.l < b.l;
if(ar != br)return a.r < b.r;
return a.t < b.t;
void add(int x, int& res)
if(cnt[x] == 0)res ++ ;
cnt[x] ++ ;
void del(int x, int& res)
cnt[x] -- ;
if(cnt[x] == 0)res -- ;
int main()
n = read(), m = read();
for(register int i = 1; i <= n; ++ i) w[i] = read();
int mq = 0, mc = 0;
for(register int i = 1; i <= m; ++ i)
char op[2];
int l, r;
scanf("%s", op);
l = read(), r = read();
if(op[0] == 'Q')
q[ ++ mq] = (Query)mq, l, r, mc;
else
c[ ++ mc] = (Modify)l, r;
//这里block一定要加1,可能出现0的情况导致除0发生浮点错误
//block=ceil(exp((log(n)+log(mc))/3));//分块大小
//block = cbrt(n * mc);
//block = pow(n * n, 1.0 / 3);
//block = pow(n, 2.0 / 3);
for(int i = 1; i <= n; ++ i)
bi[i] = (i - 1) / block;
sort(q + 1, q + 1 + mq, cmp);
for(register int k = 1, i = 0, j = 1, t = 0, res = 0; k <= mq; ++ k)
int id = q[k].id, l = q[k].l, r = q[k].r, tim = q[k].t;
//先处理x轴
/*
while(i < r)add(w[ ++ i], res);
while(i > r)del(w[i -- ], res);
while(j < l)del(w[j ++ ], res);
while(j > l)add(w[ -- j], res);
*/
while(i < r)res += ++ cnt[w[ ++ i]]