BFGS - Python实现
Posted LOGAN_XIONG
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了BFGS - Python实现相关的知识,希望对你有一定的参考价值。
- 算法特征:
利用函数$f(\\vec{x})$的1阶信息, 构造其近似的二阶Hessian矩阵. 结合Armijo Rule, 在最优化过程中达到超线性收敛的目的. - 算法推导:
为书写方便, 引入如下两个符号$B$、$D$分别表示近似Hessian矩阵及其逆矩阵:
\\begin{equation}\\label{eq_1}
B \\approx H; \\quad D \\approx H^{-1}
\\end{equation}
注意, $B$与$D$均为对称矩阵.
考虑第$k$步迭代, 将其与第$k-1$步迭代的优化变量及梯度之差分别记为$\\vec{s}_k$、$\\vec{y}_k$:
\\begin{equation}\\label{eq_2}
\\vec{s}_k = \\vec{x}_k - \\vec{x}_{k-1} \\\\
\\vec{y}_k = \\nabla{f(\\vec{x}_k)} - \\nabla{f(\\vec{x}_{k-1})}
\\end{equation}
引入割线条件(类似于微分中值定理):
\\begin{equation}\\label{eq_3}
\\vec{y}_k = B_k \\cdot \\vec{s}_k
\\end{equation}
因此有:
\\begin{equation}\\label{eq_4}
D_k \\cdot \\vec{y}_k = \\vec{s}_k
\\end{equation}
在相邻两步迭代过程中, 采用Frobenius范数衡量矩阵之变化. 为增强近似Hessian矩阵的稳定性, 考虑近似Hessian矩阵遵循保守变化, 即在满足约束条件的情况下, 相邻两步迭代过程中$B$或$D$的变化越小越好. 由此抽象出一个优化问题如下(以下忽略矢量符号):
\\begin{equation}\\label{eq_5}
\\begin{split}
\\min\\quad &\\left \\| D_k - D_{k-1}\\right \\|_F^2\\\\
\\mathrm{s.t.}
\\quad &D_k \\cdot y_k = s_k\\\\
\\quad &D_k\\text{ is symmetric}
\\end{split}
\\end{equation}
其中, $D_k$为优化变量, 代表第$k$步迭代近似Hessian矩阵的逆矩阵. 该优化问题的最优解形式如下(笔者也不太确定, 大家有能力的可以验证一下):
\\begin{equation}\\label{eq_6}
D_k = (I - \\rho_ks_ky_k^T)D_{k-1}(I - \\rho_ky_ks_k^T) + \\rho_ks_ks_k^T
\\end{equation}
其中, $\\rho_k = (y_k^Ts_k)^{-1}$. - 代码实现:
 View Code
View Code1 # BFGS算法实现 2 # 通过Armijo Rule确定迭代步长 3 4 import numpy 5 from matplotlib import pyplot as plt 6 7 8 # 目标函数0阶信息 9 def func(x1, x2): 10 funcVal = 5 * x1 ** 2 + 2 * x2 ** 2 + 3 * x1 - 10 * x2 + 4 11 return funcVal 12 # 目标函数1阶信息 13 def grad(x1, x2): 14 gradVal = numpy.array([[10 * x1 + 3], [4 * x2 - 10]]) 15 return gradVal 16 17 18 class BFGS(object): 19 20 def __init__(self, seed=None, epsilon=1.e-6, maxIter=300): 21 self.__seed = seed # 迭代起点 22 self.__epsilon = epsilon # 计算精度 23 self.__maxIter = maxIter # 最大迭代次数 24 25 self.__xPath = list() # 记录优化变量之路径 26 self.__fPath = list() # 记录目标函数值之路径 27 28 29 def solve(self): 30 self.__init_path() 31 32 xCurr = self.__init_seed(self.__seed) 33 fCurr = func(xCurr[0, 0], xCurr[1, 0]) 34 gCurr = grad(xCurr[0, 0], xCurr[1, 0]) 35 DCurr = self.__init_D(xCurr.shape[0]) # 矩阵D初始化 ~ 此处采用单位矩阵 36 self.__save_path(xCurr, fCurr) 37 38 for i in range(self.__maxIter): 39 if self.__is_converged(gCurr): 40 self.__print_MSG() 41 break 42 43 dCurr = -numpy.matmul(DCurr, gCurr) 44 alpha = self.__calc_alpha_by_ArmijoRule(xCurr, fCurr, gCurr, dCurr) 45 46 xNext = xCurr + alpha * dCurr 47 fNext = func(xNext[0, 0], xNext[1, 0]) 48 gNext = grad(xNext[0, 0], xNext[1, 0]) 49 DNext = self.__update_D_by_BFGS(xCurr, gCurr, xNext, gNext, DCurr) 50 51 xCurr, fCurr, gCurr, DCurr = xNext, fNext, gNext, DNext 52 self.__save_path(xCurr, fCurr) 53 else: 54 if self.__is_converged(gCurr): 55 self.__print_MSG() 56 else: 57 print("BFGS not converged after {} steps!".format(self.__maxIter)) 58 59 60 def show(self): 61 if not self.__xPath: 62 self.solve() 63 64 fig = plt.figure(figsize=(10, 4)) 65 ax1 = plt.subplot(1, 2, 1) 66 ax2 = plt.subplot(1, 2, 2) 67 68 ax1.plot(numpy.arange(len(self.__fPath)), self.__fPath, "k.") 69 ax1.plot(0, self.__fPath[0], "go", label="starting point") 70 ax1.plot(len(self.__fPath) - 1, self.__fPath[-1], "r*", label="solution") 71 ax1.set(xlabel="$iterCnt$", ylabel="$iterVal$") 72 ax1.legend() 73 74 x1 = numpy.linspace(-100, 100, 500) 75 x2 = numpy.linspace(-100, 100, 500) 76 x1, x2 = numpy.meshgrid(x1, x2) 77 f = func(x1, x2) 78 ax2.contour(x1, x2, f, levels=36) 79 x1Path = list(item[0] for item in self.__xPath) 80 x2Path = list(item[1] for item in self.__xPath) 81 ax2.plot(x1Path, x2Path, "k--", lw=2) 82 ax2.plot(x1Path[0], x2Path[0], "go", label="starting point") 83 ax2.plot(x1Path[-1], x2Path[-1], "r*", label="solution") 84 ax2.set(xlabel="$x_1$", ylabel="$x_2$") 85 ax2.legend() 86 87 fig.tight_layout() 88 fig.savefig("bfgs.png", dpi=300) 89 plt.close() 90 91 92 def __print_MSG(self): 93 print("Iteration steps: {}".format(len(self.__xPath) - 1)) 94 print("Seed: {}".format(self.__xPath[0].reshape(-1))) 95 print("Solution: {}".format(self.__xPath[-1].reshape(-1))) 96 97 98 def __is_converged(self, gCurr): 99 if numpy.linalg.norm(gCurr) <= self.__epsilon: 100 return True 101 return False 102 103 104 def __update_D_by_BFGS(self, xCurr, gCurr, xNext, gNext, DCurr): 105 sk = xNext - xCurr 106 yk = gNext - gCurr 107 rk = 1 / numpy.matmul(yk.T, sk)[0, 0] 108 109 term1 = rk * numpy.matmul(sk, yk.T) 110 term2 = rk * numpy.matmul(yk, sk.T) 111 I = numpy.identity(term1.shape[0]) 112 term3 = numpy.matmul(I - term1, DCurr) 113 term4 = numpy.matmul(term3, I - term2) 114 term5 = rk * numpy.matmul(sk, sk.T) 115 116 Dk = term4 + term5 117 return Dk 118 119 120 def __calc_alpha_by_ArmijoRule(self, xCurr, fCurr, gCurr, dCurr, c=1.e-4, v=0.5): 121 i = 0 122 alpha = v ** i 123 xNext = xCurr + alpha * dCurr 124 fNext = func(xNext[0, 0], xNext[1, 0]) 125 126 while True: 127 if fNext <= fCurr + c * alpha * numpy.matmul(dCurr.T, gCurr)[0, 0]: break 128 i += 1 129 alpha = v ** i 130 xNext = xCurr + alpha * dCurr 131 fNext = func(xNext[0, 0], xNext[1, 0]) 132 133 return alpha 134 135 136 def __init_D(self, n): 137 D = numpy.identity(n) 138 return D 139 140 141 def __init_seed(self, seed): 142 if seed is None: 143 seed = numpy.random.uniform(-100, 100, 2) 144 145 seed = numpy.array(seed).reshape((2, 1)) 146 return seed 147 148 149 def __init_path(self): 150 self.__xPath.clear() 151 self.__fPath.clear() 152 153 154 def __save_path(self, xCurr, fCurr): 155 self.__xPath.append(xCurr) 156 self.__fPath.append(fCurr) 157 158 159 160 if __name__ == "__main__": 161 obj = BFGS() 162 obj.solve() 163 obj.show()
笔者所用示例函数为:
\\begin{equation}\\label{eq_7}
f(x_1, x_2) = 5x_1^2 + 2x_2^2 + 3x_1 - 10x_2 + 4
\\end{equation} - 结果展示:
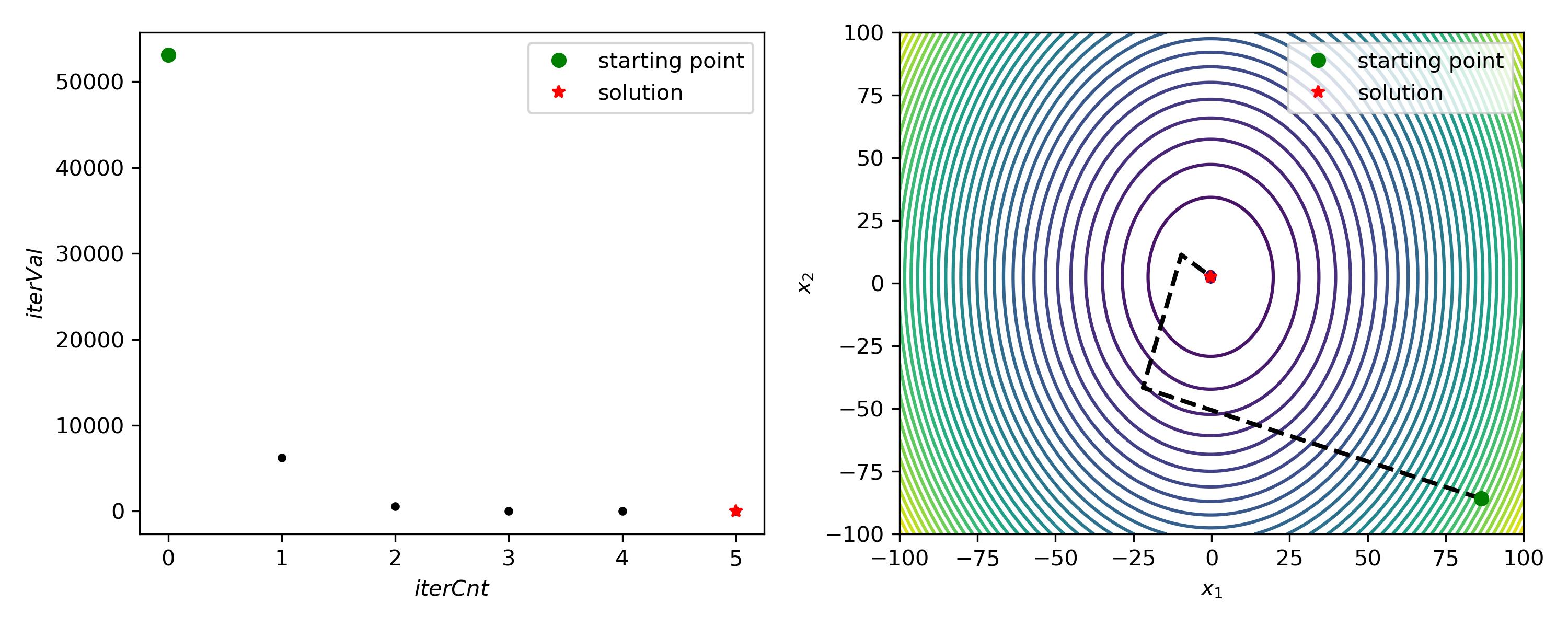
- 使用建议:
1. BFGS作为一种拟牛顿法, 主要用于无法直接获取目标函数准确Hessian矩阵的情形. 此时退而求其次, 采用BFGS的更新方式获取目标函数的近似Hessian矩阵.
2. 需要注意的是, Hessian矩阵反映函数本身的曲率信息, 因此对函数响应的噪声部分非常敏感. 如果函数响应自带噪声, 则需要采用一定的光滑手段处理之. - 参考文档:
http://aria42.com/blog/2014/12/understanding-lbfgs
https://blog.csdn.net/itplus/article/details/21897443
以上是关于BFGS - Python实现的主要内容,如果未能解决你的问题,请参考以下文章
采用Armjio准则求步长的BFGS/DFP拟牛顿方法--MATLAB实现
矩阵未对齐错误:Python SciPy fmin_bfgs
