前缀和与差分

Posted 2023-04-30 邪童的博客

前缀和与差分

前缀和

原数组: a1 , a2 , a3 , \\(\\cdots\\) , an

前缀和数组: si = a1 + a2 + \\(\\cdots\\) + ai , s0 = 0

① 如何求前缀和数组 Si : Si = Si-1 + ai , s0 = 0

② 前缀和数组的作用: 快速地求出原数组中一段数的和

一维前缀和

S[i] = S[i-1] + a[i] = a[1] + a[2] + \\(\\cdots\\) + a[i]

a[l] + \\(\\cdots\\) + a[r] = S[r] - S[l-1]

二维前缀和

S[i,j] 表示 a[i,j] 左上角全部元素的和

S[i,j] = a[i,j] + S[i-1,j] + S[i,j-1] - S[i-1,j-1]

二位前缀和的作用: 快速求出矩阵数组中子矩阵的和

a[x1,y1] (左上角) 到 a[x2,y2] (右下角) 的矩阵的元素之和为:

S[x2,y2] - S[x2,y1-1] - S[x1-1,y2] + S[x1-1,y1-1]

---

差分

差分, 即前缀和的逆运算

原数组: a1 , a2 , a3 , \\(\\cdots\\) , an

构造差分数组: b1 , b2 , b3 , \\(\\cdots\\) , bn

使得 ai = b1 + b2 + \\(\\cdots\\) + bi

一维差分

构造 bi = ai - ai-1 , a0 = 0

b1 = a1

b2 = a2 - a1

b3 = a3 - a2

\\(\\quad\\) \\(\\cdots\\)

bn = an - an-1

由差分数组 b[] 可推原数组 a[]

ai = b1 + b2 + \\(\\cdots\\) + bi

操作: 对数组 a[] , 区间 [l,r] 内所有数加 c

只需 b[l] += c , b[r+1] -= c

ai = b1 + b2 + \\(\\cdots\\) + bi

思想: 原数组 a[] 全 0 , 差分数组 b[] 也全 0

给 a[1] 赋值 a1 \\(\\Leftrightarrow\\) 对区间 [1,1] 内数加 a1 \\(\\Leftrightarrow\\) b1 += a1 , b2 -= a1

void insert (int l,int r,int c)

    b[l]+=c;
    b[r+1]-=c;

初始化: insert (i,i,a[i])

二维差分

原数组 a[i][j] , 构造差分数组 S[i][j]

a[i][j] 表示 S[i][j] 左上角全部元素之和

S[i][j] + = c \\(\\longrightarrow\\) a[i][j] 右下角所有元素加 c

给 a[x1,y1] (左上角) 到 a[x2,y2] (右下角) 的矩阵内所有元素加上 c :

b[x1][y1] += c , b[x2+1][y1] -= c , b[x1][y2+1] -= c , b[x2+1][y2+1] += c

void insert (int x1,int y1,int x2,int y2,int c)

    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;

初始化: insert(i,j,i,j,a[i][j])

前缀和与差分数组

前缀和与差分数组

基本概念

• 前缀和

我们有一个数组，如果我们要知道区间 [L, R] 的和，通常的做法是遍历一遍；这种做法在访问次数比较少的情况下或许可以，但是当我们需要多次访问时，若访问 m 次，时间复杂度为 O(m * n)。
而利用前缀和（空间换时间的方式），构造一个数组 sum，数组元素记录该索引之前（包括该索引）的数组元素之和。我们只需要通过 sum[R] - sum[L - 1] 就能求出指定范围之和。若访问 m 次，时间复杂度为 O(m)。

for (int i = 1; i <= n; i++) {
    sum[i] = sum[i - 1] + arr[i];
}

• 差分数组

如果我们需要对数组的一个区间进行频繁增减，通常的做法是在遍历的同时进行增减，这种做法的时间复杂度为 O(N)。而引入差分数组，我们只需要的时间复杂度为 O(1)。

for (int i = 1; i < n; i++) {
    diff[i] = nums[i] - nums[i - 1];
}

Leetcode 例题

303.区域和检索-数组不可变
思路解析：
我们自己定义一个数组 sums，将 sums[0] 设为 0，sums[i] 表示从 num[0] 到 num[i - 1] 累加和。

class NumArray {
public:
    vector<int> sums;
    NumArray(vector<int>& nums) {
        int len = nums.size();
        sums.resize(len + 1);
        for (int i = 1; i <= len; i++) {
            sums[i] = sums[i - 1] + nums[i - 1];
        }
    }
    
    int sumRange(int left, int right) {
        return sums[right + 1] - sums[left];
    }
};

560.和为K的子数组

思路解析：

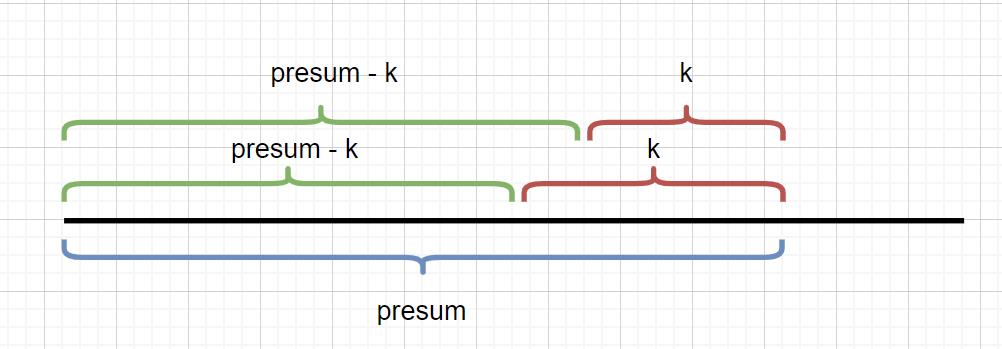
pre[j - 1] == pre[i] - k

我们考虑以 i 结尾的和为 k 的连续子数组个数时只要统计有多少个前缀和为 pre[i] - k 的 pre[j] 即可。我们建立哈希表 mp，以和为键，出现次数为对应的值，记录 pre[i] 出现的次数，从左往右边更新 mp 边计算答案，那么以 i 结尾的答案 mp[pre[i]−k] 即可在 O(1) 时间内得到。最后的答案即为所有下标结尾的和为 k 的子数组个数之和。

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> hash;
        int sum = 0, cnt = 0;
        hash[0] = 1;
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
            if (hash[sum - k]) cnt += hash[sum - k];
            hash[sum]++;
        }
        return cnt;
    }
};

304.二维区域和检索-矩阵不可变

思路解析：
负雪明烛题解

class NumMatrix {
public:
    vector<vector<int>>preSum;
    NumMatrix(vector<vector<int>>& matrix) {
        if(matrix.empty()){
            return ;
        }
        int n=matrix.size();
        int m=matrix[0].size();
        preSum.resize(n+1);
        for(int i=0;i<n+1;i++){
            preSum[i].resize(m+1);
        }
        if (n> 0) {
            for (int i = 0; i <n; i++) {
                for (int j = 0; j <m; j++) {
                    preSum[i+1][j+1] = preSum[i][j+1] + preSum[i+1][j] - preSum[i][j] + matrix[i][j];
                }
            }
        }
    }
    int sumRegion(int row1, int col1, int row2, int col2) {
        return preSum[row2 + 1][col2 + 1] - preSum[row2 + 1][col1] - preSum[row1][col2 + 1] + preSum[row1][col1];
    }
};

1094.拼车

class Solution {
public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        if (trips.empty()) {
            return false;
        }
        const int MAX_PASSNUM = 1001;
        vector<int> changeNum(MAX_PASSNUM, 0);
        for (int i = 0; i < trips.size(); i++) {
            changeNum[trips[i][1]] += trips[i][0];
            changeNum[trips[i][2]] -= trips[i][0];
        }
        int sum = 0;
        for (int j = 0; j < changeNum.size(); j++) {
            sum += changeNum[j];
            if (sum > capacity) {
                return false;
            }
        }
        return true;
    }
};

1109.航班预定统计

class Solution {
public:
    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {

        vector<int> relust(n+1, 0); 
        int diff = 0;
        for(int i = 0; i < bookings.size(); i++){
            int k = bookings[i][0]-1;                
            diff = bookings[i][2];
            relust[k] += diff;
            int j = bookings[i][1];
            relust[j] -= diff;
            }
            

        for(int i = 1; i < n; i++){
            relust[i] += relust[i-1];
        }

        relust.pop_back();
        return relust;
    }
};

原文地址：http://www.bcysf.cn/index.php/archives/6/