题解 CF1817F Entangled Substrings

Posted 2023-04-30 xiaolilsq

写点东西证明我还在搞哦爱！

题解 CF1817F Entangled Substrings

闲话：这场开始看 A 看错题了，打了好久发现样例都过不了，自闭了，不想打了，然后听 JV 的看 E，感觉 E 很奇怪，于是看 F，本来不打算做了发现 F 好像很可做的样子，于是就写了一发 F，但是最后回来 BC 都没做出来，还是输了/ll

这题题意很简单，给定串 \\(s\\)，询问有多少个有序串对 \\((a,b)\\) 满足 \\(a,b\\) 都是 \\(s\\) 的子串，并且存在可以为空的串 \\(c\\)，使得 \\(a,b\\) 在 \\(s\\) 中出现仅以 \\(acb\\) 的形式。数据范围 \\(1\\le|s|\\le 10^5\\)。

提到子串的出现次数考虑建立 SAM，在 SAM 上很容易求出每个节点对应的若干子串在 \\(s\\) 中的出现次数，我们考虑每个合法串对 \\((a,b)\\) 在 \\(acb\\) 对应节点的位置统计，这样容易发现不会遗漏。

考虑 \\(s\\) 的某个子串 \\(t\\) 要拆成合法的 \\(acb\\)，相当于是要找到 \\(t\\) 的一个前缀 \\(a\\) 出现次数和 \\(t\\) 相等，一个后缀 \\(b\\) 出现次数和 \\(t\\) 相等。这里有个细节点在单串构建的 SAM 上就是 \\(b\\) 作为 \\(t\\) 的后缀出现次数和 \\(t\\) 相等当且仅当 \\(b\\) 和 \\(t\\) 在同一个节点上，这个在构造 SAM 的时候很好归纳证明。

接下来考虑对于某个 \\(t\\) 如何找到合法的 \\(a\\)，\\(a\\) 要是 \\(t\\) 的前缀那么从 \\(a\\) 对应的节点出发行走若干步一定可以走到 \\(t\\) 对应的节点，而 \\(a\\) 出现次数要和 \\(t\\) 出现次数相同那么这条路径上面的所有节点出现次数都应该是相同的。我们考虑这样一张图，SAM 上的一条有向边保留当且仅当它连接的两个节点出现次数相同。事实上，你会发现这张图有一个特别的性质，就是它其实是一棵内向森林！证明也很简单，如果一个节点保留的出边有至少两条，那么这个节点出现次数就至少是这些出边节点出现次数之和，那么它出现次数就不可能和任意一个保留的出边节点出现次数相同了。

于是我们在这个内向森林中考虑，同一个节点的串一起考虑，对于某个节点 \\(v\\) 以及其某个祖先 \\(u\\)，考虑贡献如下图：


关键变成如何统计这个东西，容易发现 \\(u\\) 每次往上一层 \\(len_pa_u\\) 最多增加 \\(1\\)，而 \\(dis\\) 必然增加 \\(1\\)，所以后面 \\(\\max(0,*)\\) 不取 \\(0\\) 对应的恰好是树上的一段前缀，开个桶就很好统计了。

好久没复习字符串了不太熟了，写了好久想了好久。。。

下面是代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=100005;
int son[maxn*2][26],pa[maxn*2],len[maxn*2],vis[maxn*2],tot;
int extend(int p,int o)
	int now=++tot;len[now]=len[p]+1;
	while(~p&&!son[p][o])son[p][o]=now,p=pa[p];
	if(!~p)pa[now]=0;elseint d=son[p][o];
		if(len[d]==len[p]+1)pa[now]=d;else
			int _d=++tot;len[_d]=len[p]+1;
			for(int i=0;i<26;++i)son[_d][i]=son[d][i];
			while(~p&&son[p][o]==d)son[p][o]=_d,p=pa[p];
			pa[_d]=pa[d];pa[d]=pa[now]=_d;
		
	
	return now;

char s[maxn];
int SON[maxn*2],BRO[maxn*2],FA[maxn*2];
void Addson(int u,int v)
	BRO[v]=SON[u],SON[u]=v;FA[v]=u;

void update(int u)
	for(int v=SON[u];v;v=BRO[v])
		update(v);vis[u]+=vis[v];
	

int st[maxn],tp;
long long ans=0;
long long CNT[maxn*2],SUM[maxn*2];
void dfs(int u,int depth,long long tc,long long ts)
	++CNT[depth+len[pa[u]]];
	SUM[depth+len[pa[u]]]-=depth+len[pa[u]];
	tc+=CNT[depth];ts+=SUM[depth];
	ans+=1ll*(len[u]-len[pa[u]])*(tc*depth+ts);
	for(int v=SON[u];v;v=BRO[v])
		dfs(v,depth+1,tc,ts);
	
	tc-=CNT[depth];ts-=SUM[depth];
	--CNT[depth+len[pa[u]]];
	SUM[depth+len[pa[u]]]+=depth+len[pa[u]];

int main()
	pa[0]=-1;
	scanf("%s",s+1);
	int n=strlen(s+1);
	++vis[0];
	for(int i=1,p=0;i<=n;++i)
		++vis[p=extend(p,s[i]-\'a\')];
	for(int i=1;i<=tot;++i)
		Addson(pa[i],i);
	update(0);
	for(int i=0;i<=tot;++i)
		SON[i]=BRO[i]=FA[i]=0;
	for(int i=0;i<=tot;++i)
		for(int j=0;j<26;++j)
			if(son[i][j]&&vis[son[i][j]]==vis[i])
				Addson(son[i][j],i);
	for(int i=0;i<=tot;++i)
		if(!FA[i])dfs(i,0,0,0);
	printf("%lld\\n",ans);
	return 0;

Multiple Qubits and Entangled States

Single Qubit Superposition

量子态可以通过一些unitary transformation转变为叠加态量子态。

如Hardmard Gate就可以将$|0⟩$转变为叠加态$q_0$。
$H|0⟩=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{-1}{\sqrt{2}}\end{array}\right)\left(\begin{array}{l}1\\ 0\end{array}\right)=\left(\begin{array}{l}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)$

$|q_0⟩=\frac{1}{\sqrt{2}}|0⟩+\frac{1}{\sqrt{2}}|1⟩$

有趣的是，量子计算机中的任何操作均是可逆的(reversible)，这也就意味着，叠加态$|q_0⟩$可以通过变化再重新变回$|0⟩$。

这里我们只需要对$q_0$再进行一次Hardmard变换即可。

$H|q_0⟩=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{-1}{\sqrt{2}}\end{array}\right)\left(\begin{array}{l}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right)=\left(\begin{array}{l}1\\ 0\end{array}\right)$

对于叠加态，如$|q_0⟩$，我们在测量时会有50%的概率得到0，50%的概率得到1。这里的概率是由振幅决定的，振幅的平方即是概率。对于$|q_0⟩$，$|0⟩$的振幅为$\frac{1}{\sqrt{2}}$。

这里的测量，是在01坐标系下来看结果的，如果我们变更坐标系，得到的结果又将不同。

我们通过qiskit来进行测量一下。

from qiskit import QuantumCircuit, Aer, assemble
from math import pi
import numpy as np
from qiskit.visualization import plot_histogram, plot_bloch_multivector
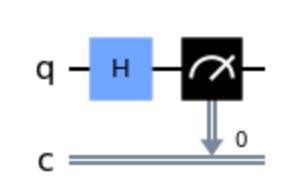
qc = QuantumCircuit(1,1)
qc.h([0])
qc.measure(0,0)
qc.draw("mpl")

# use local simulator
qasm_sim = Aer.get_backend('qasm_simulator')
qobj = assemble(qc)
results = qasm_sim.run(qobj,shots = 1).result()
answer = results.get_counts()

plot_histogram(answer)

这里设置为测量一次，结果自然是一种。图中为1。

若测量1024次，结果就接近50%的均分。

Multiple Qubits Superposition

以上讨论了单个qubit的系统，对于多个qubit呢？

qc = QuantumCircuit(2,2)
# Apply H-gate and measure to each qubit:
for qubit in range(2):
    qc.h(qubit)
    qc.measure(qubit,qubit)
qc.draw('mpl')

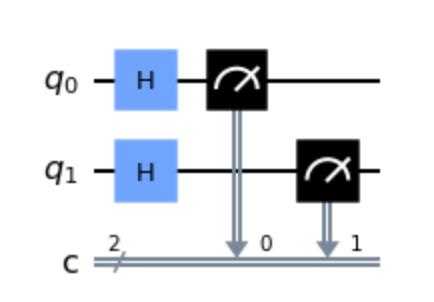
测量1024次，我们得到的结果仍然接近均分。

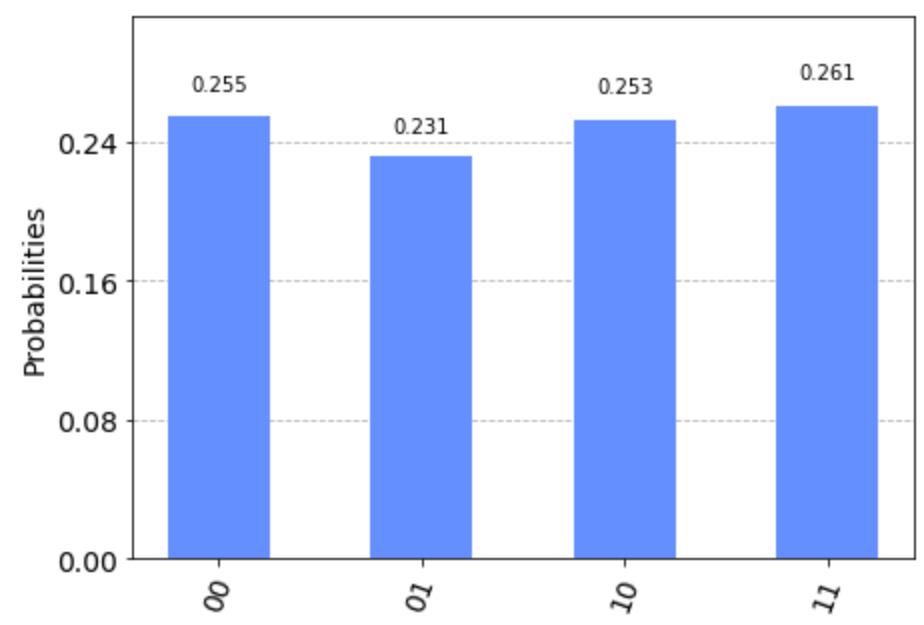
这里是为什么呢？我们用数学来推导。

首先对于multiple Qubits的表示方法，我们需要借助tensor product。
基本规则如下，如初始状态 ∣ 00 ⟩ = ∣ 0 ⟩ ⊗ ∣ 0 ⟩ |00\\rangle=|0\\rangle \\otimes|0\\rangle Codeforces 1817F

Multiple Qubits and Entangled States

Multiple Qubits and Entangled States

Multiple Qubits and Entangled States

Controllable Unsupervised Text Attribute Transfer via Editing Entangled Latent Representation

CF1512D Corrupted Array 题解