[ML从入门到入门] 支持向量机:SMO算法的收敛性分析
Posted CookMyCode
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[ML从入门到入门] 支持向量机:SMO算法的收敛性分析相关的知识,希望对你有一定的参考价值。
引言
上一篇文章我们介绍了 SMO 算法,作为其姊妹篇,本文将对 SMO 算法的收敛性进行扼要地分析,同时,希望能为读者提供新的角度去理解 SMO 算法的原理。
证明思路来自于《Convergence of a Generalized SMO Algorithm for SVM Classifier Design》。
回顾 KKT 条件
本节将从另一个角度去回顾 SVM 中的 KKT 条件,并做一些新的定义。这里不再赘述 SVM 的推导过程,我们继续沿用上一篇文章得到的结论和部分定义,需要注意一些定义会有改动。
首先,还是熟悉的 SVM 原问题的对偶问题,现在我们重新将它看作原问题:

定义出拉格朗日函数 $L$:

先求出 $L$ 对每个分量 $\\alpha_k$ 的偏导函数:

然后得到 KKT 条件:

结合偏导为零的方程和互补松弛条件,进一步推出 KKT 成立时的一个必要条件:

这其实就是之前推导 SMO 的文章里,“$\\alpha_i$ 和 $u_i$ 的关系”这一小节中提到的内容,稍微转换一下就可以得到一模一样的结果,只是偏置 $b$ 在这里变成了 $\\beta$。
我们对 $y_i$、$\\alpha_i$ 各种可能的取值进行分类,并做如下定义:

进一步简化 KKT 的必要条件:

这个条件在 SMO 中,被用于判断 $\\alpha$ 是否取得最优解,但通常 SMO 只能取到最优解的近似值,为了不让算法一直循环下去,我们需要引入一个 容忍参数(Tolerance Parameter)让算法提前停止,记作 $\\tau$。
则 SMO 取得近似解的必要条件重新记作:

如果满足上面条件,我们称为 $\\tau$-optimal,否则称为 $\\tau$-violating。
SMO 的最小化步长
我们知道,SMO 每次迭代是在 $\\alpha$ 中选择两个 $\\tau$-violating 的分量进行优化,其他分量暂时固定不变。
设选取 $\\alpha_i$ 作为第一个变量,选取 $\\alpha_j$ 作为第二个变量,SVM 优化问题的等式约束记作:

使用 $t$ 来表示某次迭代中 $\\alpha$ 的变化量,由上面的等式可以得到以下函数:

为方便书写,接下来使用 $\\alpha_ij$ 表示向量 $(\\alpha_i,\\alpha_j)$,同理,$\\alpha_ij(t)$ 表示向量 $(\\alpha_i(t),\\alpha_j(t))$;使用 $\\alpha_ij(0)$ 表示满足 $\\tau$-violating 的旧值;$\\alpha_ij(t^*)$ 表示满足 $\\tau$-optimal 的新值。
下图分别展示了 $y_i=y_j$、 $y_i\\ne y_j$ 时,$\\alpha_ij(0)$ 和 $\\alpha_ij(t^*)$ 的变化关系:

可以看到,不管 $y_i$、$y_j$ 是否相等,$\\alpha_ij(0)$ 和 $\\alpha_ij(t^*)$ 的模始终都为 $\\left| t \\right|\\sqrt2$,即:

接着我们把目标函数 $f(\\alpha)$ 考虑进来,在三维空间中得到 $y_i\\ne y_j$ 时的函数图像如下:
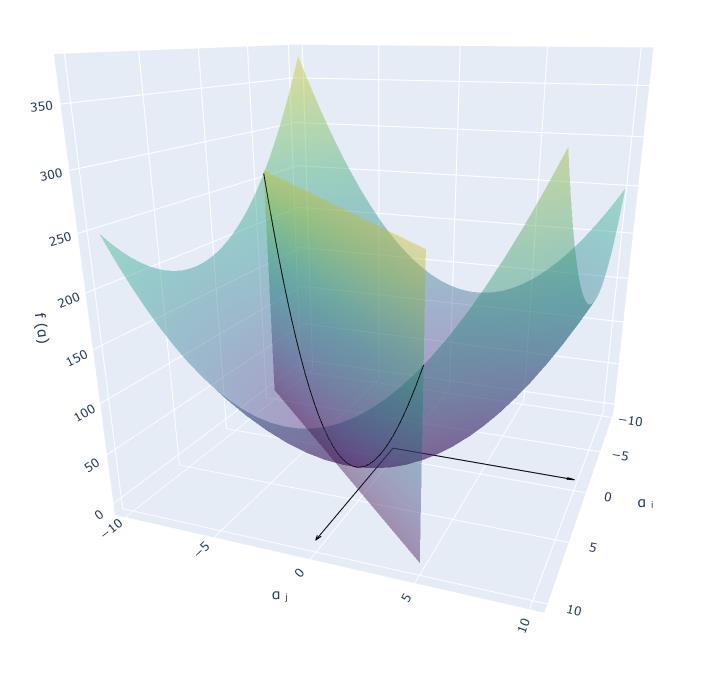
因为目标函数的核矩阵具有半正定性,所以 $f(\\alpha)$ 始终大于等于零,其表现为一个下凹的碗状曲面,最小值点位于原点;限制条件的等式约束则体现为一个平面,与目标函数相交于一条曲线,优化目标是从这条曲线上取得最小值点。结合前面我们定义的变化量 $t$,接下来用 $\\phi(t)=f\\left(\\alpha(t)\\right)$ 表示两个面相交的曲线。

由于存在另一个不等式约束,$\\alpha_i$、$\\alpha_j$ 必须大于等于零,如上图所示,最小值点 $\\alpha_ij(t^*)$ 只会在 $\\alpha_i$ 轴或 $\\alpha_j$ 轴的正半轴上取得。此时,$\\phi(t^*)\'\\le 0$。
同理,当 $y_i=y_j$ 时,得到函数图像如下:

如上图所示,当 $y_i=y_j$ 时,最小值点 $\\alpha_ij(t^*)$ 在第一象限内取得。此时,$\\phi(t^*)\'= 0$。
接下来重点对曲线 $\\phi(t)$ 进行分析,我们将 $\\phi(t)$ 泰勒展开,得:

由于 $\\alpha(t)$ 是线性函数,所以 $\\phi(t)$ 仍然是一个凸函数,又因为凸函数的二阶导是一个常数,三阶导则为零,易得:
$\\phi\'(t)=\\phi\'(0)+\\phi\'\'(0)t$
我们具体推导一下 $\\phi\'(t)$:

这是一个有意思的结论:
$\\phi\'(t)=F_i\\left(\\alpha(t)\\right)-F_j\\left(\\alpha(t)\\right)$
我们设 $i\\in I_up(\\alpha)$,$j\\in I_low(\\alpha)$,每次选择 $\\tau$-violating 的 $\\alpha_ij$ 进行优化,意味着 $F_i\\left(\\alpha\\right)-F_j\\left(\\alpha\\right)<-\\tau$,也即 $\\phi\'(0)<-\\tau$,此时 $t^*$ 必然大于零。
$\\phi(t)$ 的函数图像如下:

图中 $t_Q$ 是 $\\phi(t)$ 的最小值点,但由于限制条件存在的不等式约束,当 $y_i\\ne y_j$ 时,$t^*$ 可能无法在 $t_Q$ 处取得,此时 $\\phi\'(t^*)<-\\tau$,$i\\in I_low(\\alpha)$,$j\\in I_up(\\alpha)$,$\\alpha_ij$ 将重新满足 $\\tau$-optimal。
设经过点 $(0,\\phi(0))$ 和 $(t_Q,\\phi(t_Q))$ 的线性函数为 $l(t)$,由于 $\\phi(t)$ 是凸函数,这意味着在区间 $t\\in[0,t_Q]$ 内,$\\phi(t)\\le l(t)$。根据这一定理,我们可以推出一个重要结论:

综上所述,我们可以得到 SMO 算法的最小化步长:

SMO 的收敛性证明
我们将上一节的结论,重新调整为下面的不等式:

设 $k\\in\\mathbbN$,$\\alpha_k$ 表示第 $k$ 轮迭代时的初始值,$\\alpha_k+1$ 为该轮迭代优化后的值,则:

易得:

又根据三角不等式可知:

所以:

同理,设 $p\\in\\mathbbN_+$,则有:

因为 $f(\\alpha_k)>f(\\alpha_k+p)$,且 $f(\\cdot)$ 是凸函数,这意味着当 $k$ 足够大时,存在 $\\barf$,使得 $f(\\cdot)\\to \\barf$。
于是,对于任意实数 $\\varepsilon> 0$,存在 $n\\in\\mathbbN$,使得当 $k,p>n$ 时,下面的不等式成立:

这证明了 $\\\\alpha_k\\$ 是柯西序列,该序列将会收敛。
参考资料
Convergence of a Generalized SMO Algorithm for SVM Classifier Design
支持向量机原理SMO算法原理
在SVM的前三篇里,我们优化的目标函数最终都是一个关于$\\alpha$向量的函数。而怎么极小化这个函数,求出对应的$\\alpha$向量,进而求出分离超平面我们没有讲。本篇就对优化这个关于$\\alpha$向量的函数的SMO算法做一个总结。
1. 回顾SVM优化目标函数
我们首先回顾下我们的优化目标函数:$$ \\underbrace{ min }_{\\alpha} \\frac{1}{2}\\sum\\limits_{i=1,j=1}^{m}\\alpha_i\\alpha_jy_iy_jK(x_i,x_j) - \\sum\\limits_{i=1}^{m}\\alpha_i $$ $$ s.t. \\; \\sum\\limits_{i=1}^{m}\\alpha_iy_i = 0 $$ $$0 \\leq \\alpha_i \\leq C$$
我们的解要满足的KKT条件的对偶互补条件为:$$\\alpha_{i}^{*}(y_i(w^Tx_i + b) - 1 + \\xi_i^{*}) = 0$$
根据这个KKT条件的对偶互补条件,我们有:$$\\alpha_{i}^{*} = 0 \\Rightarrow y_i(w^{*} \\bullet \\phi(x_i) + b) \\geq 1 $$ $$ 0 <\\alpha_{i}^{*} < C \\Rightarrow y_i(w^{*} \\bullet \\phi(x_i) + b) = 1 $$ $$\\alpha_{i}^{*}= C \\Rightarrow y_i(w^{*} \\bullet \\phi(x_i) + b) \\leq 1$$
由于$w^{*} = \\sum\\limits_{j=1}^{m}\\alpha_j^{*}y_j\\phi(x_j)$,我们令$g(x) = w^{*} \\bullet \\phi(x) + b =\\sum\\limits_{j=1}^{m}\\alpha_j^{*}y_jK(x, x_j)+ b^{*}$,则有: $$\\alpha_{i}^{*} = 0 \\Rightarrow y_ig(x_i) \\geq 1 $$ $$ 0 < \\alpha_{i}^{*} < C \\Rightarrow y_ig(x_i) = 1 $$ $$\\alpha_{i}^{*}= C \\Rightarrow y_ig(x_i) \\leq 1$$
2. SMO算法的基本思想
上面这个优化式子比较复杂,里面有m个变量组成的向量$\\alpha$需要在目标函数极小化的时候求出。直接优化时很难的。SMO算法则采用了一种启发式的方法。它每次只优化两个变量,将其他的变量都视为常数。由于$\\sum\\limits_{i=1}^{m}\\alpha_iy_i = 0$.假如将$\\alpha_3, \\alpha_4, ..., \\alpha_m$ 固定,那么$\\alpha_1, \\alpha_2$之间的关系也确定了。这样SMO算法将一个复杂的优化算法转化为一个比较简单的两变量优化问题。
为了后面表示方便,我们定义$K_{ij} = \\phi(x_i) \\bullet \\phi(x_j)$
由于$\\alpha_3, \\alpha_4, ..., \\alpha_m$都成了常量,所有的常量我们都从目标函数去除,这样我们上一节的目标优化函数变成下式:$$\\;\\underbrace{ min }_{\\alpha_1, \\alpha_1} \\frac{1}{2}K_{11}\\alpha_1^2 + \\frac{1}{2}K_{22}\\alpha_2^2 +y_1y_2K_{12}\\alpha_1 \\alpha_2 -(\\alpha_1 + \\alpha_2) +y_1\\alpha_1\\sum\\limits_{i=3}^{m}y_i\\alpha_iK_{i1} + y_2\\alpha_2\\sum\\limits_{i=3}^{m}y_i\\alpha_iK_{i2}$$ $$s.t. \\;\\;\\alpha_1y_1 + \\alpha_2y_2 = -\\sum\\limits_{i=3}^{m}y_i\\alpha_i = \\varsigma $$ $$0 \\leq \\alpha_i \\leq C \\;\\; i =1,2$$
3. SMO算法目标函数的优化
为了求解上面含有这两个变量的目标优化问题,我们首先分析约束条件,所有的$\\alpha_1, \\alpha_2$都要满足约束条件,然后在约束条件下求最小。
根据上面的约束条件$\\alpha_1y_1 + \\alpha_2y_2 = \\varsigma\\;\\;0 \\leq \\alpha_i \\leq C \\;\\; i =1,2$,又由于$y_1,y_2$均只能取值1或者-1, 这样$\\alpha_1, \\alpha_2$在[0,C]和[0,C]形成的盒子里面,并且两者的关系直线的斜率只能为1或者-1,也就是说$\\alpha_1, \\alpha_2$的关系直线平行于[0,C]和[0,C]形成的盒子的对角线,如下图所示:
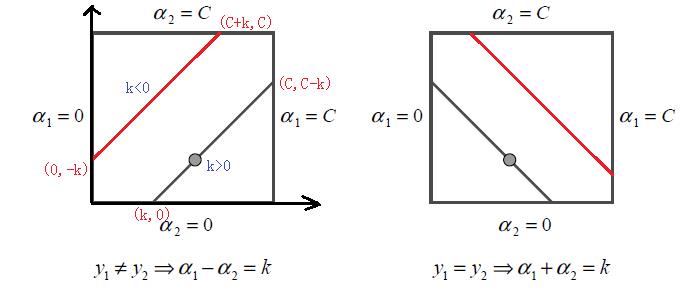
由于$\\alpha_1, \\alpha_2$的关系被限制在盒子里的一条线段上,所以两变量的优化问题实际上仅仅是一个变量的优化问题。不妨我们假设最终是$\\alpha_2$的优化问题。由于我们采用的是启发式的迭代法,假设我们上一轮迭代得到的解是$\\alpha_1^{old}, \\alpha_2^{old}$,假设沿着约束方向$\\alpha_2$未经剪辑的解是$\\alpha_2^{new,unc}$.本轮迭代完成后的解为$\\alpha_1^{new}, \\alpha_2^{new}$
由于$\\alpha_2^{new}$必须满足上图中的线段约束。假设L和H分别是上图中$\\alpha_2^{new}$所在的线段的边界。那么很显然我们有:$$L \\leq \\alpha_2^{new} \\leq H $$
而对于L和H,我们也有限制条件如果是上面左图中的情况,则$$L = max(0, \\alpha_2^{old}-\\alpha_1^{old}) \\;\\;\\;H = min(C, C+\\alpha_2^{old}-\\alpha_1^{old})$$
如果是上面右图中的情况,我们有:$$L = max(0, \\alpha_2^{old}+\\alpha_1^{old}-C) \\;\\;\\; H = min(C, \\alpha_2^{old}+\\alpha_1^{old})$$
也就是说,假如我们通过求导得到的$\\alpha_2^{new,unc}$,则最终的$\\alpha_2^{new}$应该为:
$$\\alpha_2^{new}=
\\begin{cases}
H& { \\alpha_2^{new,unc} > H}\\\\
\\alpha_2^{new,unc}& {L \\leq \\alpha_2^{new,unc} \\leq H}\\\\
L& {\\alpha_2^{new,unc} < L}
\\end{cases}$$
那么如何求出$\\alpha_2^{new,unc}$呢?很简单,我们只需要将目标函数对$\\alpha_2$求偏导数即可。
首先我们整理下我们的目标函数。
为了简化叙述,我们令$$E_i = g(x_i)-y_i = \\sum\\limits_{j=1}^{m}\\alpha_j^{*}y_jK(x_i, x_j)+ b - y_i$$,
其中$g(x)$就是我们在第一节里面的提到的$$g(x) = w^{*} \\bullet \\phi(x) + b =\\sum\\limits_{j=1}^{m}\\alpha_j^{*}y_jK(x, x_j)+ b^{*}$$
我们令$$v_i = \\sum\\limits_{j=3}^{m}y_j\\alpha_jK(x_i,x_j) = g(x_i) - \\sum\\limits_{j=1}^{2}y_j\\alpha_jK(x_i,x_j) -b $$
这样我们的优化目标函数进一步简化为:$$W(\\alpha_1,\\alpha_2) = \\frac{1}{2}K_{11}\\alpha_1^2 + \\frac{1}{2}K_{22}\\alpha_2^2 +y_1y_2K_{12}\\alpha_1 \\alpha_2 -(\\alpha_1 + \\alpha_2) +y_1\\alpha_1v_1 + y_2\\alpha_2v_2$$
由于$\\alpha_1y_1 + \\alpha_2y_2 = \\varsigma $,并且$y_i^2 = 1$,可以得到$\\alpha_1用 \\alpha_2$表达的式子为:$$\\alpha_1 = y_1(\\varsigma - \\alpha_2y_2)$$
将上式带入我们的目标优化函数,就可以消除$\\alpha_1$,得到仅仅包含$\\alpha_2$的式子。$$W(\\alpha_2) = \\frac{1}{2}K_{11}(\\varsigma - \\alpha_2y_2)^2 + \\frac{1}{2}K_{22}\\alpha_2^2 +y_2K_{12}(\\varsigma - \\alpha_2y_2) \\alpha_2 - (\\varsigma - \\alpha_2y_2)y_1 - \\alpha_2 +(\\varsigma - \\alpha_2y_2)v_1 + y_2\\alpha_2v_2$$
忙了半天,我们终于可以开始求$\\alpha_2^{new,unc}$了,现在我们开始通过求偏导数来得到$\\alpha_2^{new,unc}$。
$$\\frac{\\partial W}{\\partial \\alpha_2} = K_{11}\\alpha_2 + K_{22}\\alpha_2 -2K_{12}\\alpha_2 - K_{11}\\varsigma y_2 + K_{12}\\varsigma y_2 +y_1y_2 -1 -v_1y_2 +y_2v_2 = 0$$
整理上式有:$$(K_{11} +K_{22}-2K_{12})\\alpha_2 = y_2(y_2-y_1 + \\varsigma K_{11} - \\varsigma K_{12} + v_1 - v_2)$$
$$ = y_2(y_2-y_1 + \\varsigma K_{11} - \\varsigma K_{12} + (g(x_1) - \\sum\\limits_{j=1}^{2}y_j\\alpha_jK_{1j} -b ) -(g(x_2) - \\sum\\limits_{j=1}^{2}y_j\\alpha_jK_{2j} -b))$$
将$ \\varsigma = \\alpha_1y_1 + \\alpha_2y_2 $带入上式,我们有:
$$(K_{11} +K_{22}-2K_{12})\\alpha_2^{new,unc} = y_2((K_{11} +K_{22}-2K_{12})\\alpha_2^{old}y_2 +y_2-y_1 +g(x_1) - g(x_2))$$
$$\\;\\;\\;\\; = (K_{11} +K_{22}-2K_{12}) \\alpha_2^{old} + y_2(E_1-E_2)$$
我们终于得到了$\\alpha_2^{new,unc}$的表达式:$$\\alpha_2^{new,unc} = \\alpha_2^{old} + \\frac{y_2(E_1-E_2)}{K_{11} +K_{22}-2K_{12})}$$
利用上面讲到的$\\alpha_2^{new,unc}$和$\\alpha_2^{new}$的关系式,我们就可以得到我们新的$\\alpha_2^{new}$了。利用$\\alpha_2^{new}$和$\\alpha_1^{new}$的线性关系,我们也可以得到新的$\\alpha_1^{new}$。
4. SMO算法两个变量的选择
SMO算法需要选择合适的两个变量做迭代,其余的变量做常量来进行优化,那么怎么选择这两个变量呢?
4.1 第一个变量的选择
SMO算法称选择第一个变量为外层循环,这个变量需要选择在训练集中违反KKT条件最严重的样本点。对于每个样本点,要满足的KKT条件我们在第一节已经讲到了: $$\\alpha_{i}^{*} = 0 \\Rightarrow y_ig(x_i) \\geq 1 $$ $$ 0 < \\alpha_{i}^{*} < C \\Rightarrow y_ig(x_i) =1 $$ $$\\alpha_{i}^{*}= C \\Rightarrow y_ig(x_i) \\leq 1$$
一般来说,我们首先选择违反$0 < \\alpha_{i}^{*} < C \\Rightarrow y_ig(x_i) =1 $这个条件的点。如果这些支持向量都满足KKT条件,再选择违反$\\alpha_{i}^{*} = 0 \\Rightarrow y_ig(x_i) \\geq 1 $ 和 $\\alpha_{i}^{*}= C \\Rightarrow y_ig(x_i) \\leq 1$的点。
4.2 第二个变量的选择
SMO算法称选择第二一个变量为内层循环,假设我们在外层循环已经找到了$\\alpha_1$, 第二个变量$\\alpha_2$的选择标准是让$|E1-E2|$有足够大的变化。由于$\\alpha_1$定了的时候,$E_1$也确定了,所以要想$|E1-E2|$最大,只需要在$E_1$为正时,选择最小的$E_i$作为$E_2$, 在$E_1$为负时,选择最大的$E_i$作为$E_2$,可以将所有的$E_i$保存下来加快迭代。
如果内存循环找到的点不能让目标函数有足够的下降, 可以采用遍历支持向量点来做$\\alpha_2$,直到目标函数有足够的下降, 如果所有的支持向量做$\\alpha_2$都不能让目标函数有足够的下降,可以跳出循环,重新选择$\\alpha_1$
4.3 计算阈值b和差值$E_i$
在每次完成两个变量的优化之后,需要重新计算阈值b。当$0 < \\alpha_{1}^{new} < C$时,我们有 $$y_1 - \\sum\\limits_{i=1}^{m}\\alpha_iy_iK_{i1} -b_1 = 0 $$
于是新的$b_1^{new}$为:$$b_1^{new} = y_1 - \\sum\\limits_{i=3}^{m}\\alpha_iy_iK_{i1} - \\alpha_{1}^{new}y_1K_{11} - \\alpha_{2}^{new}y_2K_{21} $$
计算出$E_1$为:$$E_1 = g(x_1) - y_1 = \\sum\\limits_{i=3}^{m}\\alpha_iy_iK_{i1} + \\alpha_{1}^{old}y_1K_{11} + \\alpha_{2}^{old}y_2K_{21} + b^{old} -y_1$$
可以看到上两式都有$y_1 - \\sum\\limits_{i=3}^{m}\\alpha_iy_iK_{i1}$,因此可以将$b_1^{new}$用$E_1$表示为:$$b_1^{new} = -E_1 -y_1K_{11}(\\alpha_{1}^{new} - \\alpha_{1}^{old}) -y_2K_{21}(\\alpha_{2}^{new} - \\alpha_{2}^{old}) + b^{old}$$
同样的,如果$0 < \\alpha_{2}^{new} < C$, 那么有:$$b_2^{new} = -E_2 -y_1K_{12}(\\alpha_{1}^{new} - \\alpha_{1}^{old}) -y_2K_{22}(\\alpha_{2}^{new} - \\alpha_{2}^{old}) + b^{old}$$
最终的$b^{new}$为:$$b^{new} = \\frac{b_1^{new} + b_2^{new}}{2}$$
得到了$b^{new}$我们需要更新$E_i$:$$E_i = \\sum\\limits_{S}y_j\\alpha_jK(x_i,x_j) + b^{new} -y_i $$
其中,S是所有支持向量$x_j$的集合。
好了,SMO算法基本讲完了,我们来归纳下SMO算法。
5. SMO算法总结
输入是m个样本${(x_1,y_1), (x_2,y_2), ..., (x_m,y_m),}$,其中x为n维特征向量。y为二元输出,值为1,或者-1.精度e。
输出是近似解$\\alpha$
1)取初值$\\alpha^{0} = 0, k =0$
2)按照4.1节的方法选择$\\alpha_1^k$,接着按照4.2节的方法选择$\\alpha_2^k$,求出新的$\\alpha_2^{new,unc}$。$$\\alpha_2^{new,unc} = \\alpha_2^{k} + \\frac{y_2(E_1-E_2)}{K_{11} +K_{22}-2K_{12})}$$
3)按照下式求出$\\alpha_2^{k+1}$
$$\\alpha_2^{k+1}=
\\begin{cases}
H& { \\alpha_2^{new,unc} > H}\\\\
\\alpha_2^{new,unc}& {L \\leq \\alpha_2^{new,unc} \\leq H}\\\\
L& {\\alpha_2^{new,unc} < L}
\\end{cases}$$
4)利用$\\alpha_2^{k+1}$和$\\alpha_1^{k+1}$的关系求出$\\alpha_1^{k+1}$
5)按照4.3节的方法计算$b^{k+1}$和$E_i$
6)在精度e范围内检查是否满足如下的终止条件:$$\\sum\\limits_{i=1}^{m}\\alpha_iy_i = 0 $$ $$0 \\leq \\alpha_i \\leq C, i =1,2...m$$ $$\\alpha_{i}^{k+1} = 0 \\Rightarrow y_ig(x_i) \\geq 1 $$ $$ 0 <\\alpha_{i}^{k+1} < C \\Rightarrow y_ig(x_i) = 1 $$ $$\\alpha_{i}^{k+1}= C \\Rightarrow y_ig(x_i) \\leq 1$$
7)如果满足则结束,返回$\\alpha^{k+1}$,否则转到步骤2)。
SMO算法终于写完了,这块在以前学的时候是非常痛苦的,不过弄明白就豁然开朗了。希望大家也是一样。写完这一篇, SVM系列就只剩下支持向量回归了,胜利在望!
(欢迎转载,转载请注明出处。欢迎沟通交流: liujianping-ok@163.com)
以上是关于[ML从入门到入门] 支持向量机:SMO算法的收敛性分析的主要内容,如果未能解决你的问题,请参考以下文章