m基于神经网络的飞机垂直尾翼振动主动控制系统matlab仿真,包括系统辨识和在线控制
Posted 51matlab
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了m基于神经网络的飞机垂直尾翼振动主动控制系统matlab仿真,包括系统辨识和在线控制相关的知识,希望对你有一定的参考价值。
1.算法仿真效果
matlab2022a仿真结果如下:
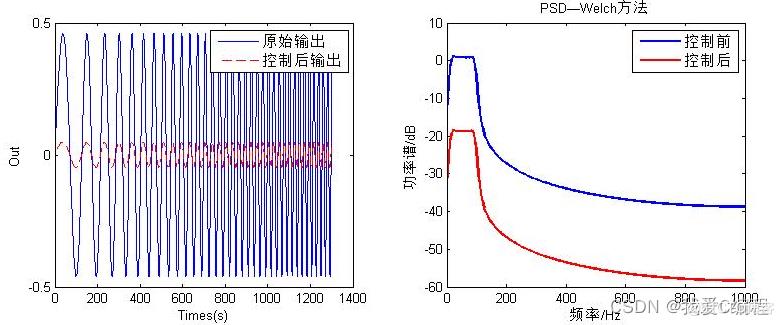
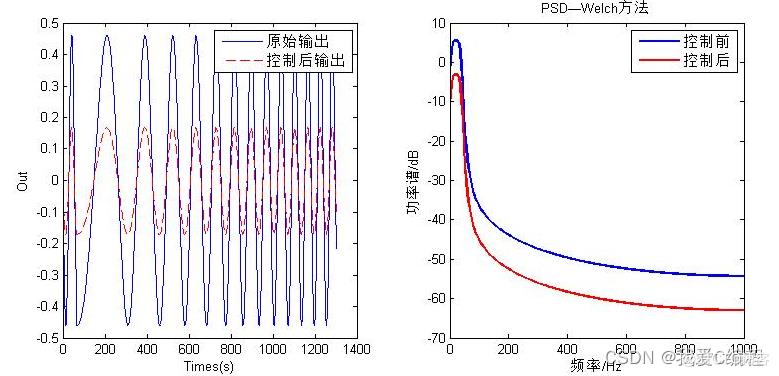
2.算法涉及理论知识概要
飞机垂直尾翼的持续涡流载荷会导致垂直尾翼的疲劳损伤,影响飞行器的飞行性能和飞行 安全,因此对尾翼进行振动主动控制是非常有必要的。以某型飞行器50%的垂尾模型为研 究对象,针对垂尾结构控制系统的不确定性和非线性等复杂特性,开展了基于人工神经网络的 垂尾结构控制系统的非线性振动模型辨识和振动主动控制研究和实验。
近年来,神经网络的研究得到了越来越多的关注和重视,神经网络以其独特的结构和信息 处理方法,已在系统辨识、信号处理、自动控制与人工智能等领域得到了实际应用。本章介绍 了人工神经网络的构成原理、BP网络和BP算法、神经网络系统辨识理论以及神经网络控制理 论,为神经网络在飞机垂尾模型智能结构振动主动控制系统中的应用奠定基础。 人工神经网络(Artificial Neural Network,简写为ANN),亦称为神经网络(Neural Network, 简写为NN),是由大量简单的处理单元(称为神经元或节点)互相连接而形成的复杂网络系统, 它反映了人脑功能的许多基本特征,是一个高度复杂的非线性动力学系统。 每个神经元代表一种特定的输出函数,称为传递函数。各神经元之间相互连接形成一个网 络拓扑,不同的神经网络模型对拓扑结构与互联模式都有一定的要求和限制。在每对神经元之 间的连接上还作用一个加权系数,这个加权系数起着生物神经系统中神经元突触强度的作用, 通常称之为连接权值。在神经网络中,连接权值可以根据经验或学习而改变,修改权值的规则 称为学习算法或学习规则。一个神经网络模型描述了一个网络如何将它的输入矢量转化为输出 矢量的过程。通常,神经网络模型的神经元特性、拓扑结构和学习算法是决定神经网络功能特 性的三大要素。
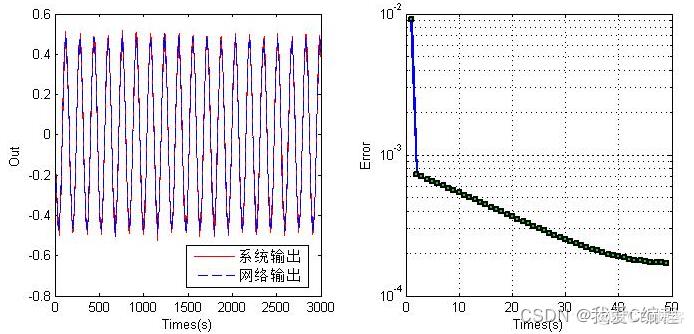
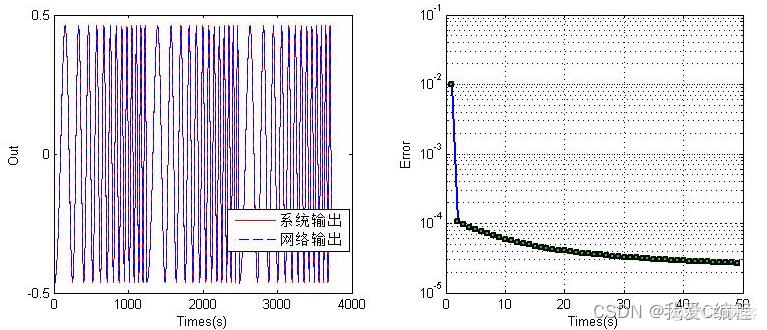
一:离线辨识
这个部分,主要是通过给定模型的输入和输出,然后通过网络进行训练,得到神经网络的辨识参数。对于网络辨识部分,其基本构架如下所示:
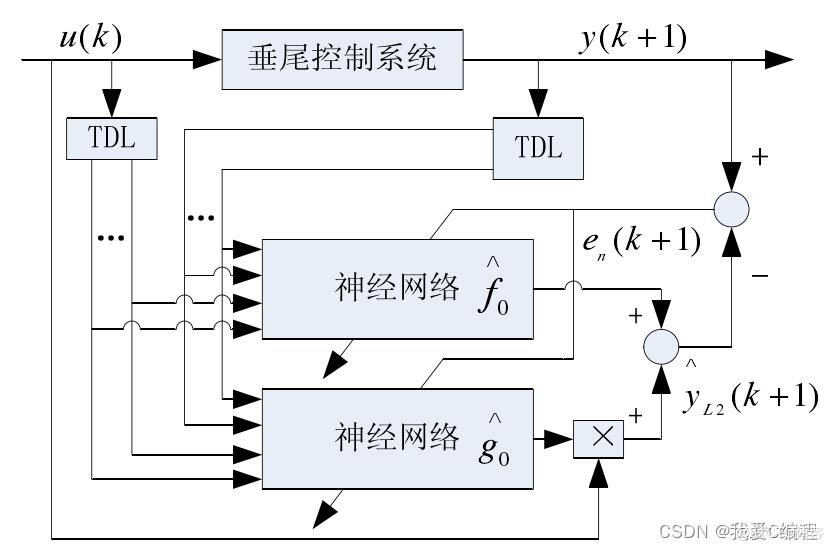
上述的辨识结构,通过控制对象的输入和输出的延迟分别进入F网络和G网络,然后通过网络输出和实际输出的误差对网络F和网络G进行在线学习。
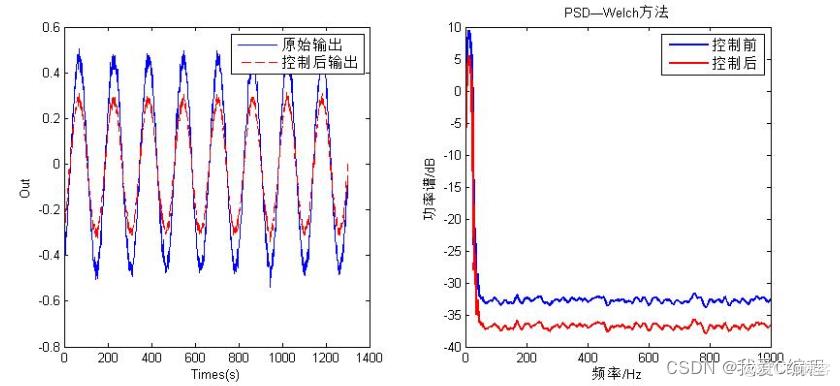
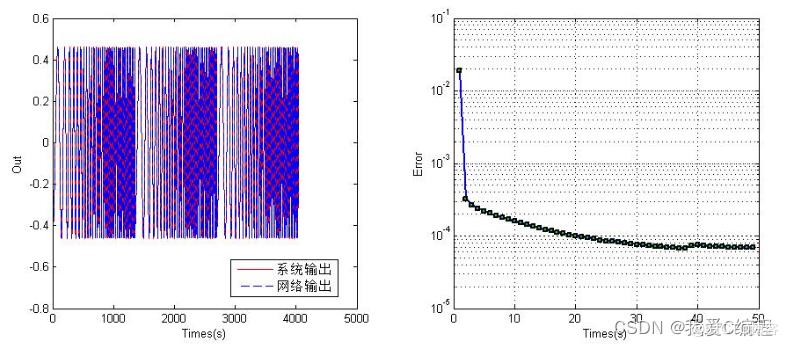
二:在线控制
这个部分主要理论为论文第四章。理论论文已经有介绍了,这里就不做叙述。其基本结构如下所示:
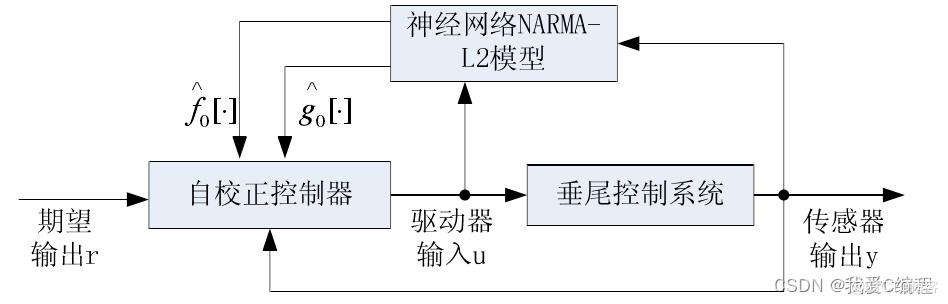
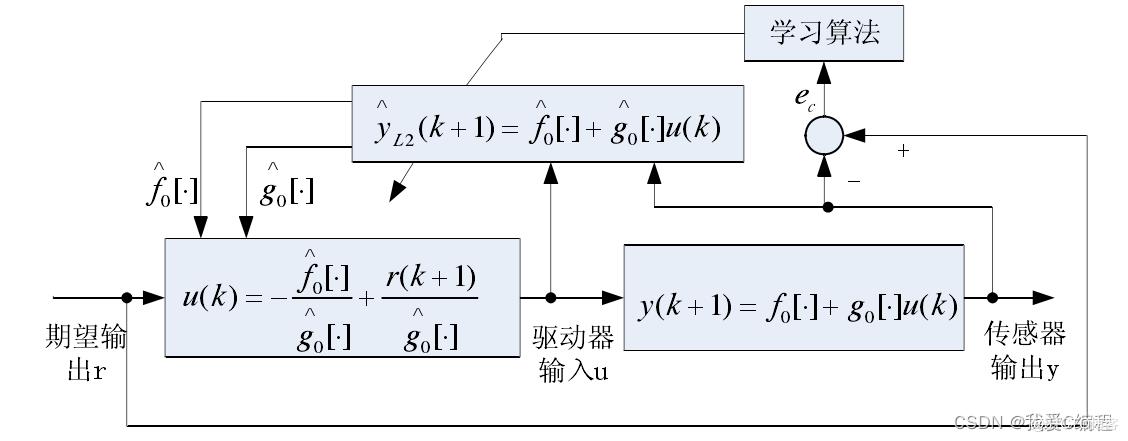
根据以上所述,设计的控制方法主要具有三大特点: 1) 计算量相对较小,适合快速实时控制系统。 2) 辨识器中的神经网络NARMA-L2模型,用离线训练方式得到, 训练方式上可以选择任意的学习批处理算法,本文采用的是Levenberg-Marquardt算法。 3) 控制系统中具有唯一的在线训练部分,即神经网络控制器的一个前馈通道,控制器对神经 网络系统模型进行重新调整。
3.MATLAB核心程序
%定义期望输出
r = Out;
parameter;
% while Iter < Max_iter
u_delay1 = 0;
u_delay2 = 0;
u_delay3 = 0;
u_delay4 = 0;
y_delay1 = 0;
y_delay2 = 0;
y_delay3 = 0;
y_delay4 = 0;
Err_tmp = 0;
for k=1:All_Length
Data_Delays = [y_delay1;
y_delay2;
y_delay3;
u_delay2;
u_delay3;
u_delay4];
%学习
[Y_hidden(k),Hidden1G,Hidden2G,Y_hiddenG(k),Hidden1F,Hidden2F,Y_hiddenF(k)] = func_Hiddern(Data_Delays,u_delay1,Num_Hidden,G_wight_In,G_wight_Inb,G_wight_Out,G_wight_Outb,F_wight_In,F_wight_Inb,F_wight_Out,F_wight_Outb);
%根据r计算u
u(k) = func_r_u_g0f0(r(k),Y_hiddenG(k),Y_hiddenF(k));
%根据辨识结果,计算输出yL
yL(k) = func_Hiddern2(u_delay1,Num_Hidden,G_wight_In0,G_wight_Inb0,G_wight_Out0,G_wight_Outb0,F_wight_In0,F_wight_Inb0,F_wight_Out0,F_wight_Outb0);
Err_tmp(k) = yL(k) - r(k);
%F和G网络
%G神经网络计算
[dg_weight_in,dg_bweight_in,dg_weight_out,dg_bweight_out] = func_G_net(Err_tmp(k),Out(k),In(k),Y_hidden(k),G_wight_Out,Hidden2G,Data_Delays,Y_hiddenG(k),Hidden1G,Num_Hidden,Num_In);
%F神经网络计算
[df_weight_in,df_bweight_in,df_weight_out,df_bweight_out] = func_F_net(Err_tmp(k),Out(k),In(k),Y_hidden(k),F_wight_Out,Hidden2F,Data_Delays,Y_hiddenG(k),Hidden1F,Num_Hidden,Num_In);
%G网络权值更新
[G_wight_In,G_wight_Out,G_wight_Inb,G_wight_Outb]=func_G_W_updata(Learn_Rate,alpha,...
G_wight_In1,G_wight_Out1,G_wight_Inb1,F_wight_Outb1,...
dg_weight_in,dg_weight_out,dg_bweight_in,dg_bweight_out,...
G_wight_Outb1,...
G_wight_In2,G_wight_Out2,G_wight_Inb2,G_wight_Outb2);
%F网络权值更新
[F_wight_In,F_wight_Out,F_wight_Inb,F_wight_Outb]=func_F_W_updata(Learn_Rate,alpha,...
G_wight_In1,F_wight_Out1,F_wight_Inb1,F_wight_Outb1,...
df_weight_in,df_weight_out,df_bweight_in,df_bweight_out,...
G_wight_In2,F_wight_Out2,F_wight_Inb2,F_wight_Outb2);
%延迟
u_delay4 = u_delay3;
u_delay3 = u_delay2;
u_delay2 = u_delay1;
u_delay1 = In(k);
y_delay4 = y_delay3;
y_delay3 = y_delay2;
y_delay2 = y_delay1;
y_delay1 = r(k);
G_wight_In2 = G_wight_In1;
G_wight_In1 = F_wight_In;
F_wight_Out2 = F_wight_Out1;
F_wight_Out1 = F_wight_Out;
F_wight_Inb2 = F_wight_Inb1;
F_wight_Inb1 = F_wight_Inb;
F_wight_Outb2 = F_wight_Outb1;
F_wight_Outb1 = F_wight_Outb;
G_wight_In2 = G_wight_In1;
G_wight_In1 = G_wight_In;
G_wight_Out2 = G_wight_Out1;
G_wight_Out1 = G_wight_Out;
G_wight_Inb2 = G_wight_Inb1;
G_wight_Inb1 = G_wight_Inb;
G_wight_Outb2 = G_wight_Outb1;
G_wight_Outb1 = G_wight_Outb;
end
figure;
subplot(121);
plot(r(end-1300:end),\'b\');
xlabel(\'Times(s)\');
ylabel(\'Out\');
hold on;
plot(yL(end-1300:end),\'r--\');
xlabel(\'Times(s)\');
ylabel(\'Out\');
legend(\'原始输出\',\'控制后输出\');
基于GRNN广义回归神经网络的飞机引擎剩余使用周期预测算法的研究
目录
作者ID :fpga和matlab
CSDN主页:https://blog.csdn.net/ccsss22?type=blog
擅长技术:
1.无线基带,无线图传,编解码
2.机器视觉,图像处理,三维重建
3.人工智能,深度学习
4.智能控制,智能优化
5.其他一、理论基础
1.1数据分析
1) unit number
2) time, in cycles
3) operational setting 1
4) operational setting 2
5) operational setting 3
6) sensor measurement 1
7) sensor measurement 2
...
26) sensor measurement 26
数据第一列是机器的编号,第二列是每个机器的运行的时间序列标号,3~5是对应的设置,6~最后一列是传感器的测量值。
数据举例:
1 1 -0.0007 -0.0004 100.0 518.67 641.82 1589.70 1400.60 14.62 21.61 554.36 2388.06 9046.19 1.30 47.47 521.66 2388.02 8138.62 8.4195 0.03 392 2388 100.00 39.06 23.4190
1 2 0.0019 -0.0003 100.0 518.67 642.15 1591.82 1403.14 14.62 21.61 553.75 2388.04 9044.07 1.30 47.49 522.28 2388.07 8131.49 8.4318 0.03 392 2388 100.00 39.00 23.4236
1 3 -0.0043 0.0003 100.0 518.67 642.35 1587.99 1404.20 14.62 21.61 554.26 2388.08 9052.94 1.30 47.27 522.42 2388.03 8133.23 8.4178 0.03 390 2388 100.00 38.95 23.3442
1 4 0.0007 0.0000 100.0 518.67 642.35 1582.79 1401.87 14.62 21.61 554.45 2388.11 9049.48 1.30 47.13 522.86 2388.08 8133.83 8.3682 0.03 392 2388 100.00 38.88 23.3739
1 5 -0.0019 -0.0002 100.0 518.67 642.37 1582.85 1406.22 14.62 21.61 554.00 2388.06 9055.15 1.30 47.28 522.19 2388.04 8133.80 8.4294 0.03 393 2388 100.00 38.90 23.4044
1 6 -0.0043 -0.0001 100.0 518.67 642.10 1584.47 1398.37 14.62 21.61 554.67 2388.02 9049.68 1.30 47.16 521.68 2388.03 8132.85 8.4108 0.03 391 2388 100.00 38.98 23.3669
1 7 0.0010 0.0001 100.0 518.67 642.48 1592.32 1397.77 14.62 21.61 554.34 2388.02 9059.13 1.30 47.36 522.32 2388.03 8132.32 8.3974 0.03 392 2388 100.00 39.10 23.3774
1 8 -0.0034 0.0003 100.0 518.67 642.56 1582.96 1400.97 14.62 21.61 553.85 2388.00 9040.80 1.30 47.24 522.47 2388.03 8131.07 8.4076 0.03 391 2388 100.00 38.97 23.3106
1 9 0.0008 0.0001 100.0 518.67 642.12 1590.98 1394.80 14.62 21.61 553.69 2388.05 9046.46 1.30 47.29 521.79 2388.05 8125.69 8.3728 0.03 392 2388 100.00 39.05 23.4066
1 10 -0.0033 0.0001 100.0 518.67 641.71 1591.24 1400.46 14.62 21.61 553.59 2388.05 9051.70 1.30 47.03 521.79 2388.06 8129.38 8.4286 0.03 393 2388 100.00 38.95 23.4694
1.2特征提取
这里,数据的维度较高,不直接使用数据进行训练,需要从数据矩阵中提取有效的特征数据作为训练特征数据。使用PCA降维算法。这个算法比较常用,主要是将高维的矩阵数据转换为低维度的特征数据。
1.3GRNN
GRNN建立在非参数核回归基础上,以样本数据为后验条件,通过执行诸如Parzen非参数估计,从观测样本里求得自变量和因变量之间的联结概率密度函数之后,直接计算出因变量对自变量的回归值。GRNN不需要设定模型的形式,但是其隐回归单元的核函数中有光滑因子,它们的取值对网络有很大影响,需优化取值。
GRNN论具有良好的函数逼近性能,而且因为其网络训练更为方便,因此,GRNN在信号过程、结构分析、控制决策系统、金融领域、生物工程领域等各个科学和工程领域得到了广泛的应用。
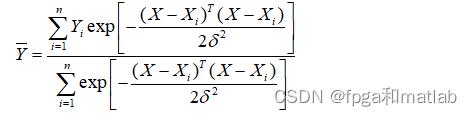
GRNN通常被用来进行函数逼近。它具有一个径向基隐含层和一个特殊的线性层。第一层和第二层的神经元数目都与输入的样本向量对的数目相等。GRNN结构如图所示,整个网络包括四层神经元:输入层、模式层、求和层与输出层。
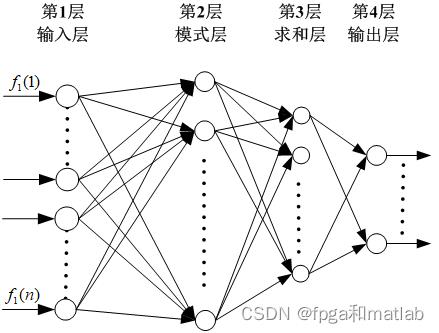
输入层的神经元数目与学习样本中输入向量的维数m相等,每个神经元都是一个简单的分布单元,这些神经元直接将输入变量传递到隐含层中。
二、核心程序
clc;
clear;
close all;
warning off;
addpath 'func\\'
%%
%Step1
STR = 1;
Name_Test = ['data\\00',num2str(STR),'\\','test_FD00',num2str(STR),'.txt'];
Name_RUL = ['data\\00',num2str(STR),'\\','RUL_FD00',num2str(STR),'.txt'];
%读取数据
Data_Test = load(Name_Test);
Data_RUL = load(Name_RUL);
%%
%Step2
%计算每个机器的时间
%得到机器编号
Mach_No = unique(Data_Test(:,1));
ind = 0;
for i = Mach_No(1):Mach_No(end)
ind = ind+1;
Index = find(Data_Test(:,1) == i);
%平滑预处理
used = [7,8,9,12,13,14,16,17,18];
tmps = Data_Test(Index,used);
[R,C] = size(tmps);
dout = zeros(R,C);
for mm = 1:C
dout(:,mm) = [func_smooth(tmps(:,mm),32)]';
end
Mach_Infoind = dout;
end
%%
%Step3
%特征提取
P = [];
for i = 1:length(Mach_No)
tmps = Mach_Infoi;
Y = func_pca(tmps',1);
Y = Y';
for j = 1:length(Y)
P = [P;Mach_Infoi(j,1:6),Y(j,:)];
end
end
%%
%Step4
%使用神经网络进行训练
load train_net.mat
y = sim(net,P');
%计算预测得到的剩余寿命
for i = 1:length(Mach_No)
if i == 1
L1 = 1;
L2 = length(Mach_Infoi);
else
L1 = L2+1;
L2 = L1+length(Mach_Infoi)-1;
end
L = L2 - L1+1;
RULs(i) = abs(round((sum(y(L1:L2))-(1+L)*L/2)/L));
end
figure;
plot(RULs,'b-o');
hold on
plot(Data_RUL,'r-o');
legend('预测结果','真实结果');
disp('误差为:');
mean(abs(RULs'-Data_RUL))
三、仿真测试结果
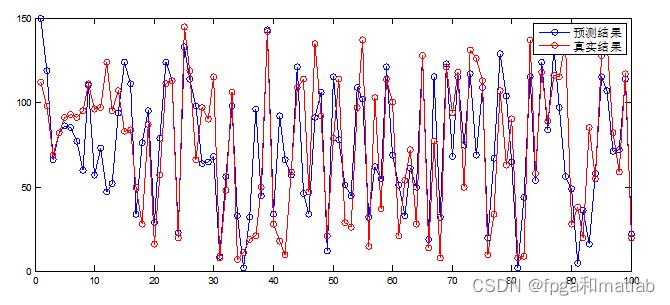
A05-21
以上是关于m基于神经网络的飞机垂直尾翼振动主动控制系统matlab仿真,包括系统辨识和在线控制的主要内容,如果未能解决你的问题,请参考以下文章