博弈论入门
Posted zwh_zzz的学习笔记
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了博弈论入门相关的知识,希望对你有一定的参考价值。
 博弈论学习
博弈论学习
博弈论
有向图游戏
Nim 游戏
Nim游戏的定义是,给定\\(n\\)堆石子,两个玩家去交替的拿石头,每次只能拿某一堆的石头,如果此时有一个玩家无法进行这个游戏了,则游戏结束。为了解决这个问题,比较直接的会先想到一个类似于\\(DP\\)的思路,考虑当前每个状态,去将其划分为两个状态,这里我们定义为\\(P:必败态\\)和\\(N : 必胜态\\),将现在的Nim游戏看作是一个有向图上进行的过程,每个结点就是现在游戏的状态(还剩多少堆,每堆还有多少个),直观的去想,出度为0的点可以直接成为\\(P\\)状态,然后我们考虑能走到最后状态的结点,是不是一定就是\\(N\\)了,因为一次操作可以直接让其走到必败,所以我们就可以类似递归的去定义,如果当前结点,他能走到的点有\\(P\\)状态,则他为\\(N\\)状态,否则为\\(P\\)状态。
但这样递归的定义复杂度是爆炸的,然后就有了一个神奇的定理,如果当前所有石子堆数异或和不为\\(0\\),则是必胜态,否则则为必败态,简单证明,全为\\(0\\)的时候异或和也同样为\\(0\\),如果此时不为\\(0\\),所以他一定是某几个二进制位产生了奇数个\\(1\\),我一定可以通过去操作某一堆来得到一个答案,把奇数个\\(1\\)给抵消掉,这样就走到\\(0\\)了。所以转移就成立了。
SG函数
通过Nim游戏,我们可以引入\\(SG\\)函数。把Nim游戏一般化,不要去思考什么堆数,现在就是在一个有向图上做游戏,终点结束游戏,定义终点值为\\(0\\),为必败,我们可以计算每个结点的\\(mex\\)值,现在也将游戏分为两个状态,一:\\(mex = 0\\),此时能走到的点不存在必败态,所以必败。反之大于0说明存在一个子结点\\(mex = 0\\),所以必胜。
现在我们把这个问题进一步复杂化,假设只是有一个无向图,而是好多个无向图,每个图上有一个棋子,表示初始状态,那我们怎么确定是否存在必胜必败关系呢?我们可以对一个有向图先去考虑这个问题,假设一个棋子的\\(SG\\)值为\\(k\\),说明 他的能走到的结点里,\\(mex\\)包括了\\(0,1,2,...,k - 1\\),这不就是Nim游戏,\\(n\\)堆石头,每次可以拿走一些,变成比他小的值,所以结论一样,异或和大于\\(0\\)必胜。
博弈论(Game Theory)入门学习笔记(持续更新)
博弈论(Game Theory)入门学习笔记(持续更新)
- 课程介绍
- 1-1 Taste-Backoff
- 1-2 Self-Interested Agents and Utility Theory
- 1-3 Define
- 1-4 Examples
- 1-5 Nash Equilibrium Intro
- 1-6 Strategic Reasoning
- 1-7 Best Response and Nash Equilibrium
- 1-8 Nash Equilibrium of Example Games
- 1-9 Dominant Strategies
- 1-10 Pareto Optimality
- 2-1 Mixed Strategies and Nash Equilibrium Taste
- 2-2 Mixed Strategies and Nash Equilibrium
- 2-3 Computing Mixed Nash Equilibrium
- 2-4 Hardness Beyond 2x2 Games
- 2-5 Example: Mixed Strategy Nash
- 2-7 Data:Professional Sports and Mixed Strategies
- 3-1 Beyond the Nash Equilibrium
- 3-2 Strictly Dominated Strategies & Iterative Removal
- 3-3 Dominated Strategies & Iterative Removal:An Application
- 3-4 Maxmin Strategies
- 3-5 Maxmin Strategies
- 3-5 Correlated Equilibrium:Intuition
- 4-1 Perfect Information Extensive Form:Taste
- 4-2 Formalizing Perfect Information Extensive Form Games
- 4-3 Perfect Information Extensive Form:Strategies,BR,NE
- 4-4 Subgame Perfection
课程介绍
- 博弈论,又称对策论,是使用严谨的数学模型研究冲突对抗条件下最优决策问题的理论,是研究竞争的逻辑和规律的数学分支。
1-1 Taste-Backoff
- 以一个经典案例引出博弈论
- TCP Backoff Game
两台电脑之间想要实现通信,两种方式可供选择,建立回退机制以及不建立回退机制。如果AB双方均建立回退机制,则双方延迟都是1。如果A、B一方建立回退机制,另一方不建立,那么建立的一方延迟是4,不建立的一方延迟是0。如果双方都不建立回退机制,则双方延迟都是3。
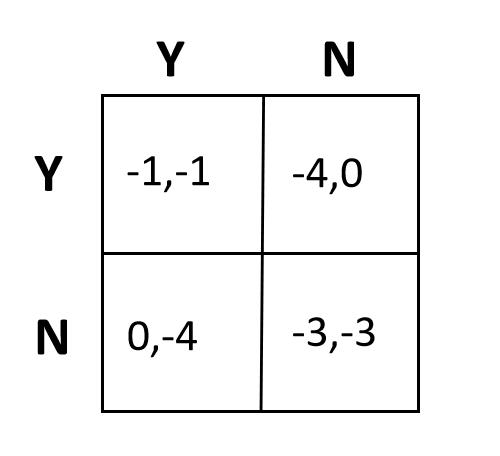
- 该问题的结果有一特点,即自己做出决策的收益不仅跟自己的决策有关,还跟对方的决策有关。因此存在一种“博弈”竞争关系。
1-2 Self-Interested Agents and Utility Theory
- Self-Interested Agents:利己代理
并不是说决策者只考虑自己或者伤害他人,而是指决策者对于世界状态有自己的独特看法,并且根据自己的判断理解做出决策。 - Utility Theory :效用理论
每个决策者都有自己的效用函数,表达了决策者对于决策的偏好,决策者做出决策都是为了最大化效用期望。
1-3 Define
-
Key Ingredients 关键组成
Players:决策者。执行决策的人。
Actions:动作。决策者可以做的事情。
Payoffs:回报。激励决策者的东西,决策带来的回报。 -
Two Standard Representations 两种标准表达方式
Normal Form:分别定义Players、Actions、Payoffs。
Extensive Form:扩展定义Timing、Information。 -
简单的博弈论问题可以使用矩阵表达,如1-1所示。
-
复杂问题无法用矩阵表达,如经典的造反问题。共有10000000个人,每个人可以选择造反或者不造反,只有达到2000000个人才算造反成功。如果造反达到人数要求,无论决策者选择什么收益都是1;如果造反没有达到人数要求,则决策者选择造反的收益是-1;如果造反没有达到人数要求,则决策者选择不造反的收益是0。
Players: N = { 1 , . . . , 10 , 000 , 000 } N=\\{1,...,10,000,000\\} N={1,...,10,000,000}
Actions Set for player i i i: A i = { R e v o l t , N o t } A_i=\\{Revolt,Not\\} Ai={Revolt,Not}
Utility Function for player i i i:
(1) u i ( a i ) = 1 i f { j : a j = R e v o l t } > = 2 , 000 , 000 u_i(a_i)=1 \\space if \\{j:a_j=Revolt\\}>=2,000,000 ui(ai)=1 if{j:aj=Revolt}>=2,000,000
(2) u i ( a i ) = − 1 i f { j : a j = R e v o l t } < 2 , 000 , 000 a n d a i = R e v o l t u_i(a_i)=-1 \\space if \\{j:a_j=Revolt\\}<2,000,000 \\space and \\space a_i=Revolt ui(ai)=−1 if{j:aj=Revolt}<2,000,000 and ai=Revolt
(3) u i ( a i ) = − 0 i f { j : a j = R e v o l t } < 2 , 000 , 000 a n d a i = N o t u_i(a_i)=-0 \\space if \\{j:a_j=Revolt\\}<2,000,000 \\space and \\space a_i=Not ui(ai)=−0 if{j:aj=Revolt}<2,000,000 and ai=Not
1-4 Examples
-
囚徒困境 Prisoner’s dilemma。故事背景:两个共谋犯罪的人被关入监狱,不能互相沟通情况。如果两个人都不揭发对方,则由于证据不确定,每个人都坐牢一年;若一人揭发,而另一人沉默,则揭发者因为立功而立即获释,沉默者因不合作而入狱十年;若互相揭发,则因证据确凿,二者都判刑八年。由于囚徒无法信任对方,因此倾向于互相揭发,而不是同守沉默。
结果的优劣程度按照A>B>C>D排序。
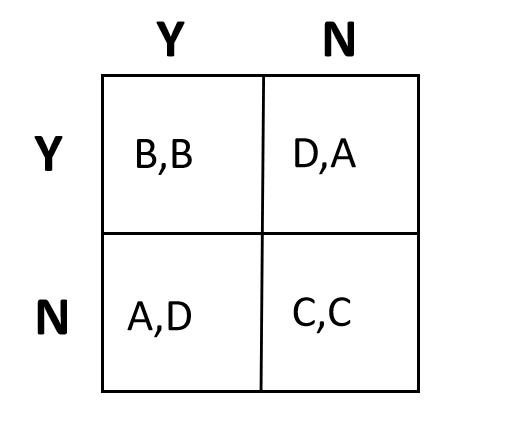
-
Game of Pure Competition 纯竞争博弈
博弈的双方具有完全对立的利益。
对于双方任意动作组合,其效用之和永远为一个常数。 ∀ a ∈ A , u 1 ( a ) + u 2 ( a ) = c \\forall \\space a \\in A,u_1(a)+u_2(a)=c ∀ a∈A,u1(a)+u2(a)=c
特殊类型:零和博弈。双方效用之和永远为0。
举例说明:石头剪刀布游戏。
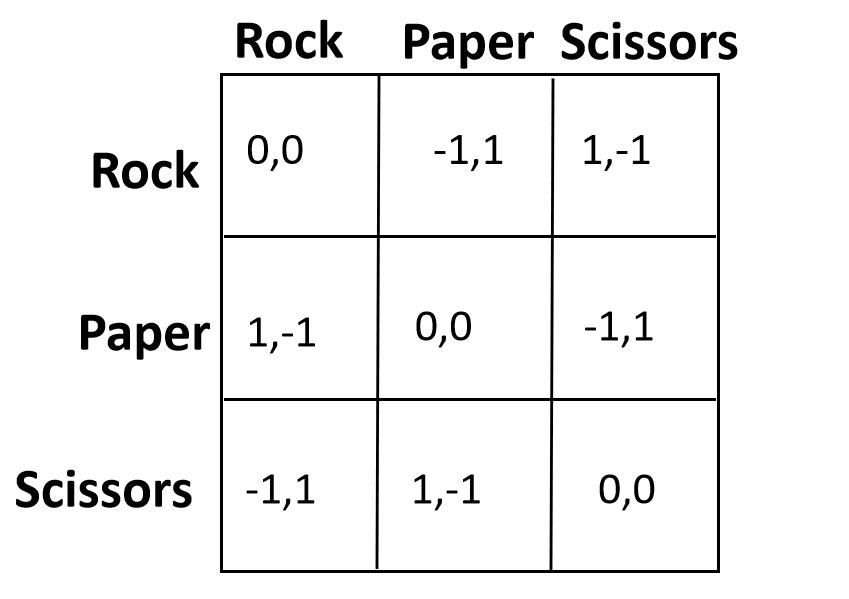
-
Games of Cooperation 合作博弈
博弈的多方具有相同的利益,利益之间不存在冲突。 ∀ a ∈ A , ∀ i , j , u i ( a ) = u j ( a ) \\forall a\\in A,\\forall i,j,u_i(a)=u_j(a) ∀a∈A,∀i,j,ui(a)=uj(a)
举例说明:过马路问题。马路两头两个人想同时通行,每个人可以选择靠左或者靠右行驶。
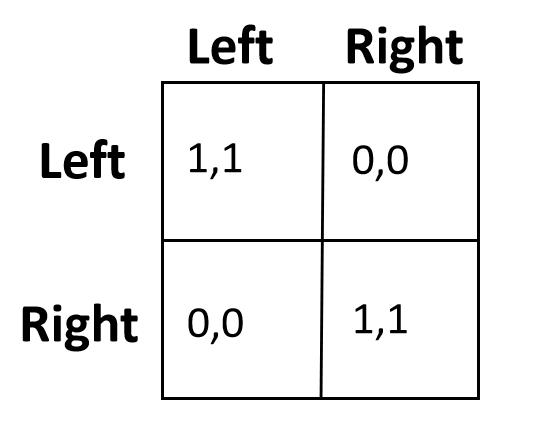
1-5 Nash Equilibrium Intro
- Keynes Beauty Contest Game:凯恩斯选美博弈
举办选美大赛,从1-100号候选者中选择自己认为最美的一位,获得票数最多的人获得选美冠军,投票给选美冠军的人也会得到一定的奖励。这个问题是老千层饼了,第一层的人只是自己觉得谁漂亮就选谁,比如A觉得10号最美投票给了10号;第二层的人考虑其他人的投票分布从而产生自己的决策,比如B觉得可能有很多人投票给30号,虽然自己喜欢10号也投票给30号;第三层的人觉得其他人可能也会因为考虑到第二层的因素,从而放弃自己最喜欢的转投自己认为最火爆的…这是一个无休止的猜想游戏。 - 猜数字游戏
每个人从1-100中选择一个整数,最后最接近平均值三分之二的人获得奖励,假设参加这项游戏的人数足够多。这个问题同样是一个千层饼问题。
第一层的人:参赛人数足够多,我假设大家所选择的数字均匀分布,那么最后的平均值应该接近于50。那么我为了获胜应该选择的数字是 50 ∗ 2 3 = 33 50*\\frac{2}{3}=33 50∗32=33。
第二层的人:我想大部分人都在第一层,因此他们都选择33。那么最后的平均值应该接近于33。那么我为了获胜应该选择的数字是 33 ∗ 2 3 = 22 33*\\frac{2}{3}=22 33∗32=22。
第三层的人: 22 ∗ 2 3 = 11 22*\\frac{2}{3}=11 22∗32=11。
…
第n层的人:应该选择的数是0。这就得到了纳什均衡。
美国进行过一项调查,其中2%选择了66(没读懂题的笨蛋)、5%的选择了50(第一层)、10%的选择了33(第二层)、6%选择了22(第三层)、12%的选择了0或者1(思考到了最后)。但最后的结果平均值为19,第三层左右的人获得了最终的胜利。 - 以上两个故事告诉我们,在投资问题或者博弈问题中,我们的层数不可太高也不可太低。太低是傻子,太高聪明反被聪明误。
1-6 Strategic Reasoning
- 在其他人的决策确定的情况下,每一个决策者都是为了最大化个人的收获效用来做出决策。
- 一旦纳什均衡建立,没有人可以通过改变决策跳出均衡而获利受益。
- 如果某些决策者通过改变决策跳出均衡可以获利受益,那么说明纳什均衡还没有真正建立。
- 纳什均衡是一个稳定的状态,但并不是一个最优的获利状态。
1-7 Best Response and Nash Equilibrium
- Best Response 最优响应
如果知道其他所有人的动作,那么挑选对于自己最有利的动作就变得十分简单。
a i 表 示 第 i 个 决 策 者 所 做 出 的 决 策 a_i表示第i个决策者所做出的决策 ai表示第i个决策者所做出的决策
a − i = { a 1 , . . . , a i − 1 , a i + 1 , . . . , a n } 表 示 除 去 a i 以 外 其 他 人 的 决 策 a_{-i}=\\{a_1,...,a_{i-1},a_{i+1},...,a_n\\}表示除去a_i以外其他人的决策 a−i={a1,...,ai−1,ai+1,...,an}表示除去ai以外其他人的决策
a = ( a i , a − i ) a=(a_i,a_{-i}) a=(ai,a−i)
a i ∗ ∈ B R ( a − i ) i f f ∀ a i ∈ A i , u i ( a i ∗ , a − i ) > = u i ( a i , a − i ) a_i^*\\in BR(a_{-i})\\space iff \\forall a_i\\in A_i,u_i(a_i^*,a_{-i})>=u_i(a_i,a_{-i}) ai∗∈BR(a−i) iff∀ai以上是关于博弈论入门的主要内容,如果未能解决你的问题,请参考以下文章