Python 汉诺塔问题

Posted 2020-11-27 Mindf

一、汉诺塔的代码

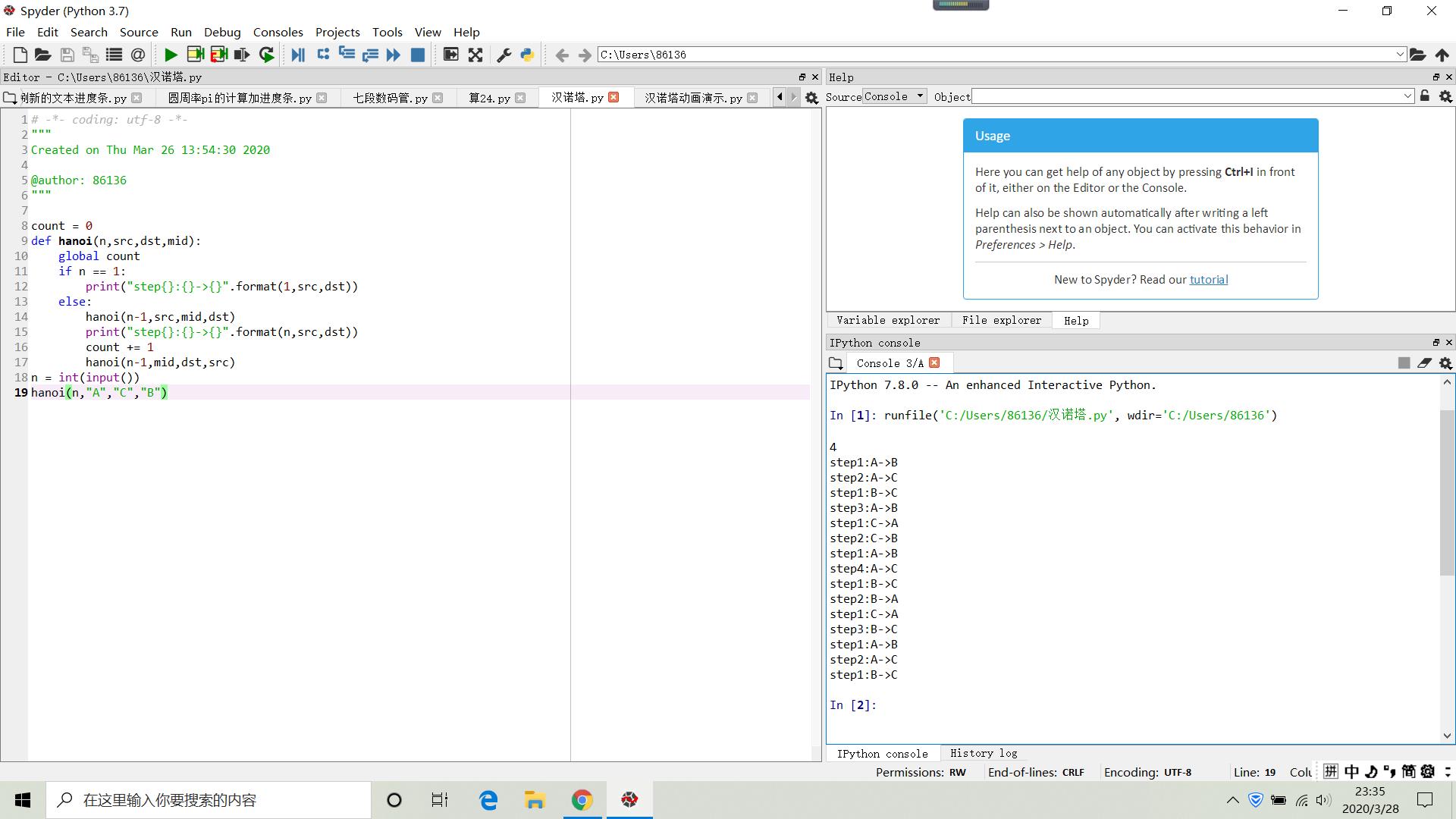
count = 0
def hanoi(n,src,dst,mid): #定义四个参数分别表示圆盘的个数、源柱子、目标柱子、中间的过渡柱子
    global count  #用global保留字实现全局变量的使用
    if n == 1:
        print("step{}:{}->{}".format(1,src,dst)) #若只有一个圆盘，则直接从源柱子移到目标柱子即可
        count += 1
    else:
        hanoi(n-1,src,mid,dst) #将n-1个圆盘从源柱子移到中间柱子
        print("step{}:{}->{}".format(n,src,dst)) #将最后一个圆盘从源柱子移到目标柱子
        count += 1
        hanoi(n-1,mid,dst,src) #将n-1个圆盘从中间柱子移到目标柱子
n = int(input())
hanoi(n,"A","C","B")

 

结果演示

二、汉诺塔的动画演示

代码引用https://blog.csdn.net/BeerBread134/article/details/69226991

代码最多能运行7阶汉诺塔，主要用了递归和栈的想法，用turtle实现。

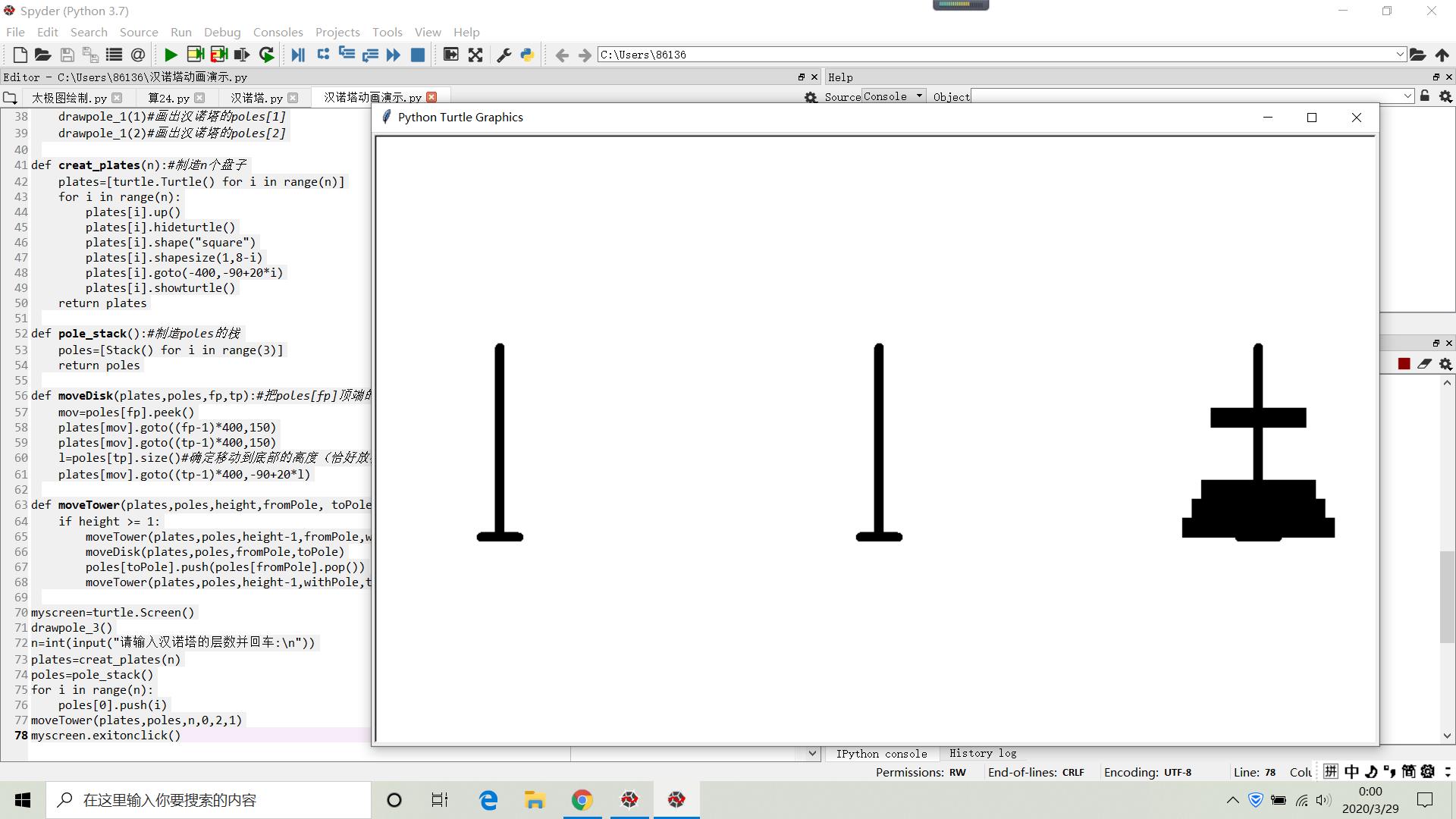
import turtle
 
class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return len(self.items) == 0
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        if not self.isEmpty():
            return self.items[len(self.items) - 1]
    def size(self):
        return len(self.items)
 
def drawpole_3():#画出汉诺塔的poles
    t = turtle.Turtle()
    t.hideturtle()
    def drawpole_1(k):
        t.up()
        t.pensize(10)
        t.speed(100)
        t.goto(400*(k-1), 100)
        t.down()
        t.goto(400*(k-1), -100)
        t.goto(400*(k-1)-20, -100)
        t.goto(400*(k-1)+20, -100)
    drawpole_1(0)#画出汉诺塔的poles[0]
    drawpole_1(1)#画出汉诺塔的poles[1]
    drawpole_1(2)#画出汉诺塔的poles[2]
 
def creat_plates(n):#制造n个盘子
    plates=[turtle.Turtle() for i in range(n)]
    for i in range(n):
        plates[i].up()
        plates[i].hideturtle()
        plates[i].shape("square")
        plates[i].shapesize(1,8-i)
        plates[i].goto(-400,-90+20*i)
        plates[i].showturtle()
    return plates
 
def pole_stack():#制造poles的栈
    poles=[Stack() for i in range(3)]
    return poles
 
def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
    mov=poles[fp].peek()
    plates[mov].goto((fp-1)*400,150)
    plates[mov].goto((tp-1)*400,150)
    l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
    plates[mov].goto((tp-1)*400,-90+20*l)
 
def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
    if height >= 1:
        moveTower(plates,poles,height-1,fromPole,withPole,toPole)
        moveDisk(plates,poles,fromPole,toPole)
        poles[toPole].push(poles[fromPole].pop())
        moveTower(plates,poles,height-1,withPole,toPole,fromPole)
 
myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
    poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()

结果显示