基于扩展卡尔曼滤波的目标跟踪仿真

Posted 2023-04-28 51matlab

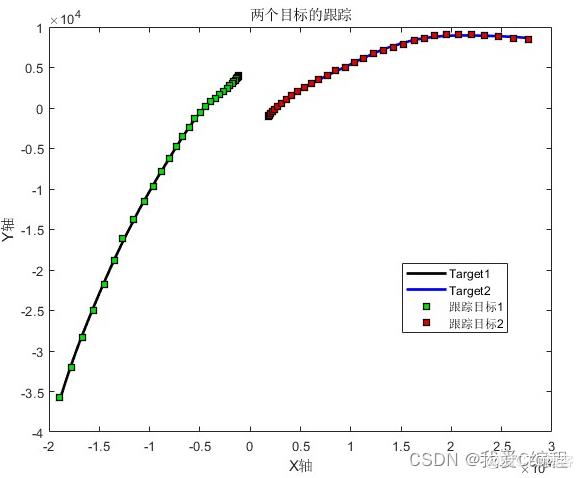
1.算法仿真效果

matlab2022a仿真结果如下：

 

 

 

2.算法涉及理论知识概要

       在WSN中，人们通过飞机撒播或手动分布等方式，把许多传感器节点随意撒播在监控区域（sensor field）中或者周边，这些传感器节点自组织组建了网络。传感器节点把感知信息通过除它之外的传感器节点进行传递，在逐跳传递时，其它很多节点也许会处理这些感知信息(比如数据融合等)，感知数据凭借多跳路由的方式抵达汇聚节点。它们最终借助卫星或Internet到管理节点。监测人员通过任务管理节点配置与管理WSN，发布监测任务及获取监测数据。

 

       一般情况下，传感器节点是一类很小的嵌入式系统。因为电池给传感器节点提供电量，所以传感器节点的计算、储蓄与通讯能力都不太强。节点的通讯长度较短，通常只与周边节点交换数据，它借助多跳路由来传递这些内容。故从网络用途的角度来考虑，所有传感器节点都具备普通网络节点的2个功能:终端与路由。所有传感器节点不只需要获取与处理信息，还需保存、管理与融合其它节点传输来的信息。它们共同合作来实现一系列功能。

 

       与普通节点相比，汇聚节点具有相对强的计算、储蓄与通讯能力。它实现了WSN与外部网络的互连，能够使2个协议栈间的通讯协议相互转变，并且广播管理节点的感知内容，最后监测到的信息被传递给互联网。汇聚节点不仅能是无通讯功能的网关仪器，而且同样能是含多用途的传感器节点。

 

       Kalman滤波能够在线性高斯模型的条件下，可以对目标的状态做出最优的估计，得到较好的跟踪效果。对非线性滤波问题常用的处理方法是利用线性化技巧将其转化为一个近似的线性滤波问题。因此，可以利用非线性函数的局部性特性，将非线性模型局部化，再利用Kalman滤波算法完成滤波跟踪。扩展Kalman滤波就是基于这样的思想，将系统的非线性函数做一阶Taylor展开，得到线性化的系统方程从而完成对目标的滤波估计等处理。非线性系统离散动态方程可以表示为

 

 

 

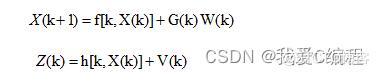
       这里为了便于数学处理，假定没有控制量的输入，并假定过程噪声是均值为零的高斯白噪声，且噪声分布矩阵   是已知的。其中，观测噪声 也是加性均值为零的高斯白噪声。假定过程噪声和观测噪声序列是彼此独立的，并且有初始状态估计 和协方差矩阵 。和线性系统的情况一样，我们可以得到扩展Kalman滤波算法如下:

 

 

 

 

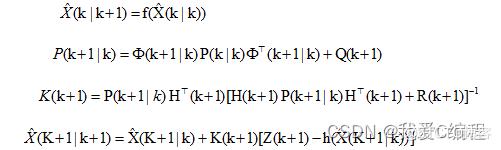
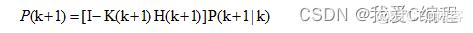
        所谓的非线性方程，就是因变量和自变量的关系不是线性的，这类方程很多，例如平方关系，对数关系，指数关系，三角函数关系等等。这类方程可分为两类，一类是多项式方程，一种是非多项式方程。为了便于说明非线性卡尔曼滤波——扩展Kalman滤波的原理，我们选用一下系统.

 

 

 

3.MATLAB核心程序

 

数计算器
for t=2:T
    % 获得两个目标的观测值      注： 观测向量 z1 和 z2 所使用的下标的数字不对应于我们下面所标示的目标
    z1(:,t)=[sqrt(True_State1(1,t)^2+True_State1(4,t)^2);atan(True_State1(4,t)/True_State1(1,t))]...
        +MNoise_Matrix*randn(2,1);
    z2(:,t)=[sqrt(True_State2(1,t)^2+True_State2(4,t)^2);atan(True_State2(4,t)/True_State2(1,t))]...
        +MNoise_Matrix*randn(2,1);
    % 分别获得两个目标的状态预测
    EKF_Pre1=F*EKalman_State1(:,t-1);
    EKF_Pre2=F*EKalman_State2(:,t-1);
    % Prediction Self-connection Matrix
    P_Pre1=F*P1*F\'+SNoise_Matrix1*Q11*SNoise_Matrix1\';
    P_Pre2=F*P2*F\'+SNoise_Matrix2*Q12*SNoise_Matrix2\';
     % Obtain Jacobian Matrix of Measurement 1
    H1=[EKF_Pre1(1)/sqrt(EKF_Pre1(1)^2+EKF_Pre1(4)^2) 0 0 EKF_Pre1(4)/sqrt(EKF_Pre1(1)^2+EKF_Pre1(4)^2) 0 0;
        -1*EKF_Pre1(4)/(EKF_Pre1(1)^2+EKF_Pre1(4)^2)  0 0   EKF_Pre1(1)/(EKF_Pre1(1)^2+EKF_Pre1(4)^2)   0 0];
    
    H2=[EKF_Pre2(1)/sqrt(EKF_Pre2(1)^2+EKF_Pre2(4)^2) 0 0 EKF_Pre2(4)/sqrt(EKF_Pre2(1)^2+EKF_Pre2(4)^2) 0 0;
        -1*EKF_Pre2(4)/(EKF_Pre2(1)^2+EKF_Pre2(4)^2)  0 0   EKF_Pre2(1)/(EKF_Pre2(1)^2+EKF_Pre2(4)^2)   0 0];
    % Obtain Prediction of Measurement
    z_Pre1=[sqrt(EKF_Pre1(1)^2+EKF_Pre1(4)^2);atan(EKF_Pre1(4)/EKF_Pre1(1))];
    z_Pre2=[sqrt(EKF_Pre2(1)^2+EKF_Pre2(4)^2);atan(EKF_Pre2(4)/EKF_Pre2(1))];
    % Obtain Extend Kalman Gain
    K1=P_Pre1*H1\'*inv(H1*P_Pre1*H1\'+MNoise_Matrix*Q21*MNoise_Matrix);
    K2=P_Pre2*H2\'*inv(H2*P_Pre2*H2\'+MNoise_Matrix*Q21*MNoise_Matrix);
    % 做两个观测数据相关处理
    piancha(:,1,1)=z1(:,t)-z_Pre1;    piancha(:,1,2)=z1(:,t)-z_Pre2;
    piancha(:,2,1)=z2(:,t)-z_Pre1;    piancha(:,2,2)=z2(:,t)-z_Pre2;
    M_S=MNoise_Matrix*MNoise_Matrix;    % 观测过程协方差矩阵
    % 选择落入每个波门里面的数据个数
    % 目标状态估计
    EKalman_State1(:,t)=EKF_Pre1+K1*(piancha(:,1,1));
    EKalman_State2(:,t)=EKF_Pre2+K2*(piancha(:,2,2));
    % 估计两个目标的各自协方差
    P1=(eye(6)-K1*H1)*P_Pre1;
    P2=(eye(6)-K2*H2)*P_Pre2;
end

 

　　

 

扩展卡尔曼滤波EKF—目标跟踪中的应用(算法部分)

扩展卡尔曼滤波EKF—目标跟踪中的应用(算法部分)

原创不易，路过的各位大佬请点个赞

机动目标跟踪/非线性滤波/传感器融合/导航等探讨代码联系WX: ZB823618313

仿真部分见博客：
扩展卡尔曼滤波EKF—目标跟踪中的应用(仿真部分)

https://blog.csdn.net/weixin_44044161/article/details/115329181             

作者:[e-mail]
备注：
扩展卡尔曼滤波算法；
目标跟踪matlab仿真实现;
Case: 二维目标跟踪情况和三维目标跟踪情况
代码下载地址如下（分别为二维情形和三维情形）

扩展卡尔曼滤波 机动目标跟踪 EKF

https://download.csdn.net/download/weixin_44044161/85401461

扩展卡尔曼滤波EKF匀速圆周运动CT

https://download.csdn.net/download/weixin_44044161/85401885

EKF仿真代码：二维目标跟踪

https://download.csdn.net/download/weixin_44044161/85123812

EKF仿真代码：三维目标跟踪

https://download.csdn.net/download/weixin_44044161/85123744

扩展卡尔曼滤波—及其在目标跟踪中的应用

• 扩展卡尔曼滤波EKF—目标跟踪中的应用(算法部分)
• • 一、带加性噪声的扩展卡尔曼滤波算法
  • • 1.1 问题描述（离散时间非线性系统描述）
    • 1.2 扩展卡尔曼滤波器（EKF）
  • 二、带非加性噪声的扩展卡尔曼滤波算法
  • • 2.1 问题描述（离散时间非线性系统描述）
    • 2.2 带非加性噪声的扩展卡尔曼滤波器（EKF）
  • 三、仿真实验
  • • 3.1 仿真场景（三维）
    • 3.2 仿真场景（二维）
    • 3.3 二维EKF跟踪仿真结果
  • 四、二维EKF跟踪参考代码
  • • 4.1 主函数

一、带加性噪声的扩展卡尔曼滤波算法

1.1 问题描述（离散时间非线性系统描述）

考虑带加性噪声的一般非线性系统模型，
$$\begin{gathered} x_k=f(x_{k-1})+w_{k-1} \\ {z}_k=h(x_k)+v_k\text{\hspace{1em}(1)} \end{gathered}$$
其中$x_k$为$k$时刻的目标状态向量。$z_k$为$k$时刻量测向量（传感器数据）。这里不考虑控制器$u_k$。$w_k$和$v_k$分别是过程噪声序列和量测噪声序列，并假设$w_k$和$v_k$为零均值高斯白噪声，其方差分别为$Q_k$和$R_k$的高斯白噪声，即$w_k\sim (0,Q_k)$, $v_k\sim (0,R_k)$，且满足如下关系(线性高斯假设)为：
$$\begin{array}{rl}E[w_i{v}_j^{\prime }]& =0\\ E[w_i{w}_j^{\prime }]& =0i\ne j\\ E[v_i{v}_j^{\prime }]& =0i\ne j\end{array}$$

1.2 扩展卡尔曼滤波器（EKF）

1.） 初始化
给定$k-1$时刻的状态估计和协方差矩阵
$${\hat{x}}_{k-1|k-1},P_{k-1|k-1},Q_{k-1},R_{k-1}$$
当为$0$时刻时，滤波器最优初始化为
$$x_0\sim ({\bar{x}}_0,P_0),Q_0,R_0$$
即$$\begin{gathered} {\hat{x}}_{0|0}={\bar{x}}_0 \\ {P}_{0|0}=P_0 \end{gathered}$$
2. ) 状态预测
2.1 计算非线性系统方程的雅可比矩阵
$$F_{k-1}=\frac{\partial f\left(x_{k-1}\right)}{\partial x_{k-1}}{|}_{x_{k-1}={\hat{x}}_{k-1|k-1}}$$
2.2 状态一步预测及预测误差协方差阵为
x ^ k ∣ k − 1 = E [ x k ∣ Z k − 1 ] ≈ E [ f k − 1 ( x ^ k −