AC 自动机学习笔记

Posted 2023-04-26 qwq-qaq-tat

前置知识：Trie 树、KMP 算法。

相信大家第一次听见这个算法都会很兴奋。

自动机，就是依据一个或者一些字符串建出来的无向图。

AC 自动机全名 Aho-Corasick Automaton。

它可以在 \\(O(\\sum|T|+|S|)\\) 的时间内解决多模式串的匹配问题。

它的本质就是在 Trie 树上跑 KMP。

AC 自动机主要有 3 个步骤。

1. 把所有的模式串建成一棵 Trie 树。

2. 把 Trie 所有节点的失配指针全部求出来。

3. 统计每个模式串 \\(T\\) 在 \\(S\\) 里出现了多少次。

依据题目讲解：【模板】AC 自动机（二次加强版）。

给出若干个字符串 \\(T\\)，依次求出它们在字符串 \\(S\\) 里出现了几次。\\(T\\) 可能重复。

\\(\\sum|T|\\le 2\\times 10^5\\)，\\(|S|\\le 2\\times 10^6\\)。

步骤 1：我们把 Trie 树建立出来。

注意我们将 0 号节点作为全树的根。

所以每加入一个串，都从 0 号节点一步步往下跳。

由于 \\(T\\) 可能重复，我们将用一个 \\(b\\) 数组记录每个模式串 \\(T\\) 的结束位置。

for(int i=1,x=0;i<=n;i++)
	scanf("%s",s+1);
	for(int j=1;s[j];j++)
		if(!t[x][s[j]-\'a\'])t[x][s[j]-\'a\']=++cnt;
		x=t[x][s[j]-\'a\'];
	
	b[i]=x;x=0;

步骤 2：我们建立失配指针。

这里是整个算法流程的重中之重，理解了它就基本上懂了。

首先，每个节点的失配指针指向什么？

这个节点失配了，那我们肯定是要继续考虑从根到这个节点组成的字符串的在 Trie 树上的最长真后缀。

怎么求出这个真后缀呢？

我们可以利用它的父亲节点的失配指针来计算。

首先，它父亲节点的失配指针就是指向它父亲的最长真后缀。

如果这个它父亲节点的失配指针指向的点有相同的儿子，就直接连上去就行了。

如果没有，那我们怎么办？

一个想法是给空节点也连上失配指针，然后一直跳直到跳到一个存在的节点为止。

复杂度爆炸。

所以我们可以把空节点加入考量。

就是即便这个节点在 Trie 树上是一个空节点，我们也要给它赋值。

怎么赋呢？

我们直接把一个空节点赋为它父亲节点的失配指针指向的点的对应儿子就行了。

如果该儿子为空，那么由于指针指向的是节点编号，所以其实是指向一个不为空的节点。

这样就不用每建一个点都要暴力上跳很多次。

由于每一个节点的失配指针都有可能只是上一层的点，所以用广搜实现。

结合图理解一下（空节点的话，有用才画出来）：

1. 这是我们建好的 Trie 树。一开始所有指针都是 0，也就是指向根节点。
   

2. 然后我们开始连边：2 号节点的父亲是 1 号节点，1 号节点的失配指针指向 0 号节点，0 号节点的 a 儿子是 1 号节点，所以 2 号节点的失陪指针指向 1 号节点。同样道理，3 号节点的父亲节点是 1 号节点，1 号节点的失配指针指向 0 号节点，0 号节点的 b 儿子是 5 号节点，所以 3 号节点的失配指针指向 5 号节点。
   

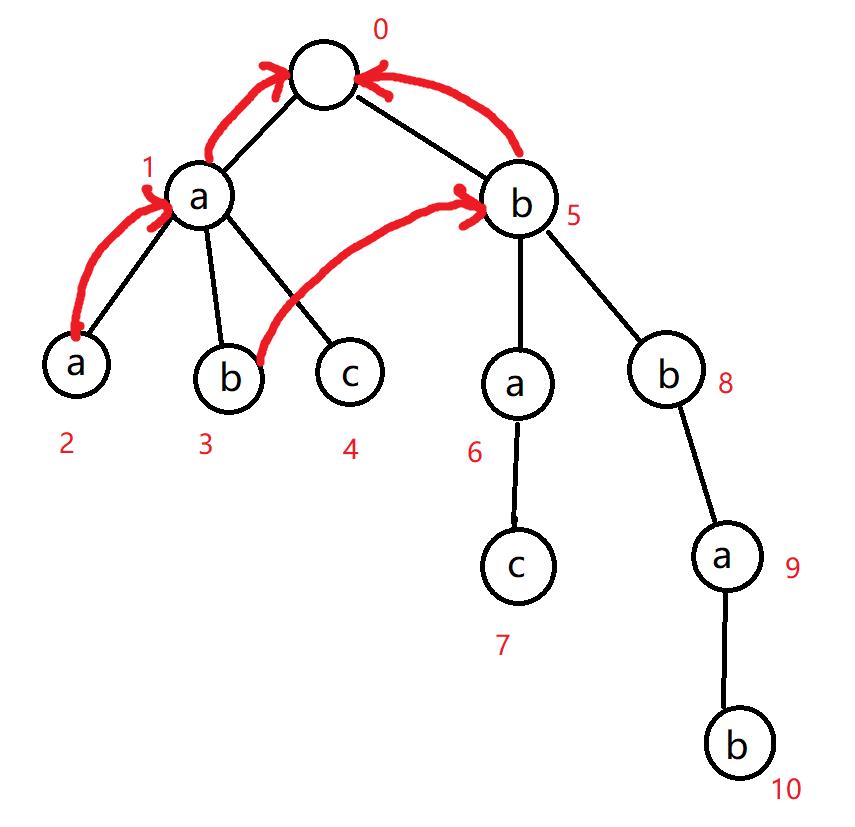
3. 接下来我们要处理 4 号节点的失配指针。它的父亲是 1 号节点，1 号节点的失配指针是 0 号节点，它的 c 儿子是空节点，那我们也要向它连边。
   

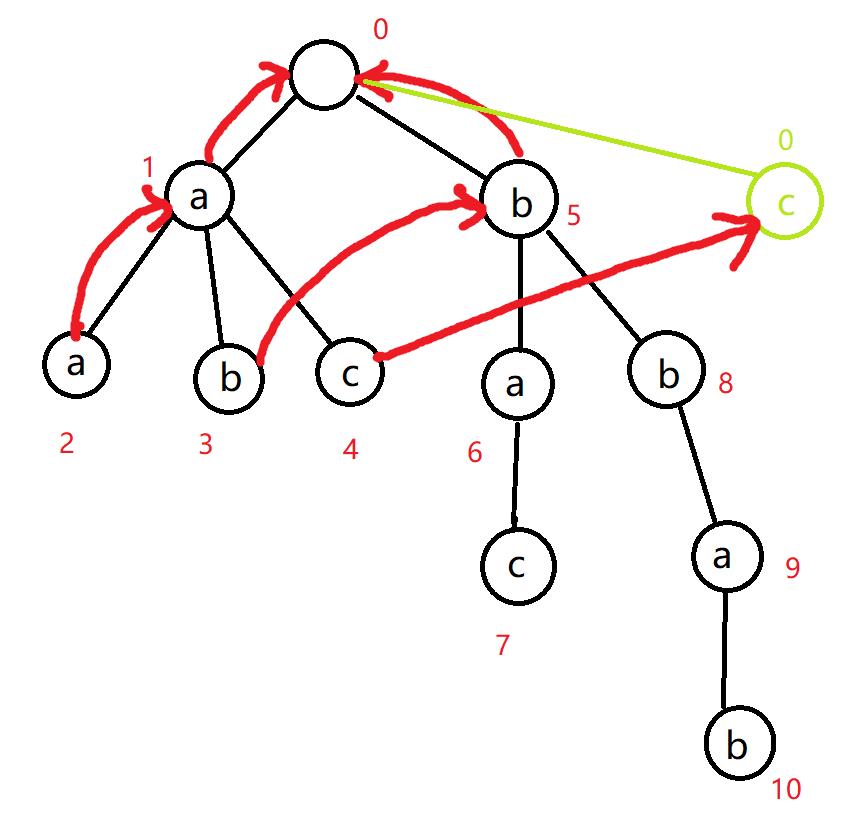
4. 由于失配指针记录的是编号，所以就相当于与 0 号节点连边。

5. 接下来继续处理，6 号节点的父亲是 5 号节点，5 号节点的失配指针指向 0 号节点，0 号节点的 a 儿子是 1 号节点，所以 6 号节点的失配指针指向 1 号节点。8 号节点的父亲是 5 号节点，5 号节点的失配指针指向 0 号节点，0 号节点的 b 儿子是 5 号节点，所以 8 号节点的失配指针指向 5 号节点。7 号节点的父亲是 6 号节点，6 号节点的失配指针指向 1 号节点，1 号节点的 c 儿子是 4 号节点，所以 7 号节点的失配指针指向 4 号节点。9 号节点的父亲是 8 号节点，8 号节点的失配指针指向 5 号节点，5 号节点的 a 儿子是 6 号节点，所以 9 号节点的失配指针指向 6 号节点。

6. 接下来继续处理，10 号节点的父亲是 9 号节点，9 号节点的失配指针指向 6 号节点，6 号节点的 b 儿子是几？6 号节点的失配指针指向 1 号节点，1 号节点的 b 儿子是 3，所以 6 号节点的 b 儿子编号也为 3（这些在处理 6 号节点时就处理了）。所以 10 号节点的失配指针指向 3 号节点。
   

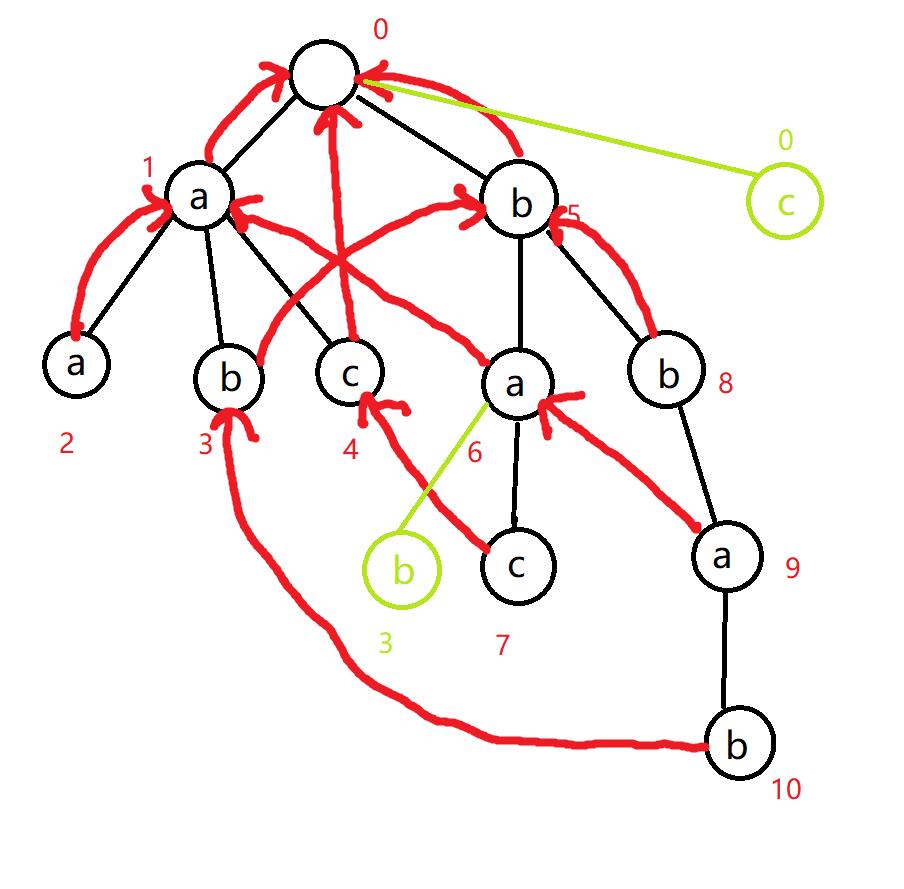
然后这个 AC 自动机就建完啦！

queue<int>q;
	for(int i=0;i<26;i++)
		if(t[0][i])q.push(t[0][i]);
	while(!q.empty())
		int x=q.front();q.pop();
		for(int i=0;i<26;i++)
			if(t[x][i])f[t[x][i]]=t[f[x]][i],q.push(t[x][i]);
			else t[x][i]=t[f[x]][i];
		
	

步骤 3：统计每个模式串出现的次数。

我们考虑统计 Trie 树上每个节点对应的字符串出现的次数。

暴力法是用 \\(S\\) 遍历整棵 Trie 树，每到一个节点就疯狂跳失配指针直到它为空，然后路径上的每一个节点的计数器都加一。

这样最坏是 \\(O(nm)\\) 的。

考虑优化。

那我们可以知道，由于每一次跳失配指针，它在 Trie 树上的深度都会变小。

而且最后指针一定会跳到 0。

那我们就发现失配指针组成了一棵根节点为 0 的树。

那就可以直接使用 \\(S\\) 遍历 Trie 树，每到一个节点就将计数器加一。

最后在失配指针树上 dfs 一下，统计每个节点的子树和就可以了。

void dfs(int x)
	for(int i=0;i<u[x].size();i++)dfs(u[x][i]),v[x]+=v[u[x][i]];

for(int x=0,i=1;s[i];i++)
	x=t[x][s[i]-\'a\'];
	v[x]++;

for(int i=1;i<=cnt;i++)u[f[i]].push_back(i);
dfs(0);
for(int i=1;i<=n;i++)write(v[b[i]]),putchar(10);

总时间复杂度、空间复杂度都是 \\(O(\\sum|T|+|S|)\\)。

但是 \\(\\sum|T|\\) 有个 26 的大常数，时间空间上都有。

AC自动机算法学习

KMP+TRIE

int val[1000100][31],tot;
int tr[1000100];
int fail[1000100];
struct AC_Trie{
    void clean(){
        tot=0;
        memset(val,0,sizeof(val));
        memset(tr,0,sizeof(tr));
        memset(fail,0,sizeof(fail));
    }
    void build(){
        queue<int> q;
        memset(fail,0,sizeof(fail));
        while(!q.empty()) q.pop();
        for(int i=0;i<26;i++) if(val[0][i]!=0) q.push(val[0][i]);
        while(!q.empty()){
            int u=q.front();q.pop();
            for(int i=0;i<26;i++){
                if(val[u][i]!=0){
                    fail[val[u][i]]=val[fail[u]][i];
                    q.push(val[u][i]); 
                }else{
                    val[u][i]=val[fail[u]][i];
                }
            }
        }
    }
    void insert(string x){
        int len=x.length(),p=0;
        for(int i=0;i<len;i++){
            int c=x[i]-'a';
            if(val[p][c]==0) tot++,val[p][c]=tot;
            p=val[p][c];
        }
        tr[p]++;
    }
    int find(string x){
        int len=x.length(),p=0,res=0;
        for(int i=0;i<len;i++){
            p=val[p][x[i]-'a'];
            for(int j=p;j&&~tr[j];j=fail[j]) res+=tr[j],tr[j]=-1;
        }
        return res;
    }
}tree;