ACM动态规划题

Posted

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了ACM动态规划题相关的知识，希望对你有一定的参考价值。

用C做，怎么做？不行的话C++也行啊
从三角形顶部到底部有很多条不同的路径，对于每条路径，把路径上面的数加起来可以得到一个和，和最大的路径称为最佳路径。任务：求最佳路径上的数字之和。

这是动态规划很经典的问题之一。。。
还有，想纠正LZ一个说法，“用C做，怎么做？不行的话C++也行啊”，感觉LZ觉得C++更厉害一些哈。。。其实不然，像LZ说的这种问题是算法问题，不基于某种编程语言的。。。
正题：
假设我们的实例是：
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
我们可以用一个整型数组max[][]来存状态（这里就是动态规划），这个状态就是从顶上走到当前数字num[i][j]时和最大的那个和max[i][j]
程序运行完例子后，max中为这样的：
7
10 15
18 16 15
20 25 20 19
24 30 27 26 24
程序如下：
#include <stdio.h>
#include <stdlib.h>

#define MAX 100
int num[MAX][MAX];
int max[MAX][MAX];
int n;

int main()
int i, j, _max;
scanf("%d", &n);
for (i=0; i<n; i++)
for (j=0; j<i+1; j++)
scanf("%d", &num[i][j]);
max[i][j] = num[i][j];

for (i=0; i<n-1; i++)
for (j=0; j<i+1; j++)
// 下一行的前一个数
if (max[i+1][j] < max[i][j] + num[i+1][j])
max[i+1][j] = max[i][j] + num[i+1][j];
// 下一行的后一个数
if (max[i+1][j+1] < max[i][j] + num[i+1][j+1])
max[i+1][j+1] = max[i][j] + num[i+1][j+1];

// 输出max[][]
for (i=0; i<n; i++)
for (j=0; j<i+1; j++)
printf("%d ", max[i][j]);
putchar('\n');

// 输出max值
_max = max[n-1][0];
for (i=1; i<n; i++)
if (_max < max[n-1][i])
_max = max[n-1][i];
printf("%d\n", _max);
system("pause");
return 0;
 参考技术A 思路是这样的
三角形中每一个点都可以从上层的两个点到达该点，假如我们知道顶点分别到上层两个点的最优路径，选择数字之和最大的那条路径就是顶点到该点的最佳路径，也就是说如果我们知道顶点到第n层中每一个点的最佳路径，那么我们就可以求出顶点到第n+1层中每一个点的最佳路径，而第一层是最优路径是已知的，最终的结果就是从底层的n条路径中选一个数值最大的就是答案 参考技术B 给楼主提供另一个思路
杨辉三角 计算权值

acm选修课——动态规划

动态规划

动态规划

动态规划

概念

求最优，
满足最优性原理：
有最优子结构，从小规模最优化到大规模最优化
又名：记忆化搜索

对比

贪心：从小到大
分治：子问题求解独立

证明

求状态转移方程的过程
就是暴力剪枝，记忆化搜索

例题

1.最长上升子序列

http://poj.org/problem?id=2533

找最长上升子序列
优化：可以想到，f[i]，第i个上升子序列的最小值，是持续递增的（反证法），以此改成了二分

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#ifdef LOCAL
FILE*fp=freopen("text.in","r",stdin);//文件忘记注释害人不浅！！ 
#endif
int a[1005],f[1005]; //第i个的最小值 
signed main(){
	int n;
	scanf("%d",&n);
	for(int i=0;i<n;i++){
		scanf("%d",&a[i]);
	}
	int cnt=0;
	memset(f,0x3f,sizeof(int)*(n+1));
	f[0]=-1;//注意边界数据。。 
	//可以想到，是持续递增的，可以以此二分 
	for(int i=0;i<n;i++){
		int l=0,r=cnt,m=(l+r)/2;//初始化 
		while(l<r){
			if(f[m]<a[i]&&f[m+1]>=a[i])break;
			if(f[m+1]<a[i])l=m+1;
			if(f[m]>=a[i])r=m;
			m=(l+r)/2;//注意顺序 
		}
		f[m+1]=a[i];
		if(m==cnt)cnt++;
		/*for(int j=cnt;j>=0;j--){
			if(f[j]<a[i]&&f[j+1]>=a[i]){
				f[j+1]=a[i];
				if(j==cnt)cnt++;
			}
		}*/
	}
	printf("%d\\n",cnt);
	return 0;
}

2.数塔

http://acm.hdu.edu.cn/showproblem.php?pid=2084
自底向上

代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int a[1005],f[1005]; //第i个的最小值 
signed main(){
	int n;
	freopen("text.in","r",stdin);
	scanf("%d",&n);
	for(int i=0;i<n;i++){
		scanf("%d",&a[i]);
	}
	int cnt=0;
	memset(f,0x3f,sizeof(int)*(n+1));
	f[0]=-1;//注意边界数据。。 
	for(int i=0;i<n;i++){
		for(int j=cnt;j>=0;j--){
			if(f[j]<a[i]&&f[j+1]>a[i]){
				f[j+1]=a[i];
				if(j==cnt)cnt++;
			}
		}
	}
	printf("%d\\n",cnt);
	return 0;
}

3.最长公共子序列

https://www.luogu.com.cn/problem/P1439

1.正常想法：

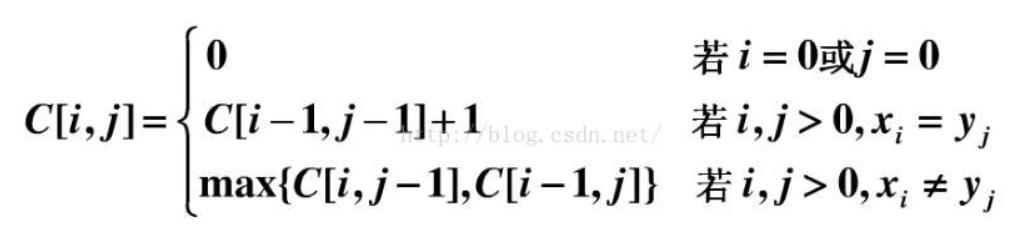
在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;
#ifdef LOCAL
FILE*fp=freopen("text.in","r",stdin);
#endif
int a[100003],b[100003],s[2][100003];//滚动数组节省空间 
int main(){
	int t;
	scanf("%d",&t);
	for(int i=1;i<=t;i++){
		scanf("%d",&a[i]);
	}
	for(int i=1;i<=t;i++){
		scanf("%d",&b[i]);
	}
	
	for(int i=1;i<=t;i++){
		s[i%2][0]=0;
		for(int j=1;j<=t;j++){
			if(a[i]==b[j]){
				s[i%2][j]=s[(i+1)%2][j-1]+1;
			}else{
				s[i%2][j]=max(s[i%2][j-1],s[(i+1)%2][j]);
			}
		}
	} 
	printf("%d\\n",s[t%2][t]);
	return 0;
}

2.这里数据量大，利用不重复，化二公共匹配为按另一个一个中顺序为优先级的一上升子序列为好

#include<bits/stdc++.h>
#ifdef LOCAL
FILE*fp=freopen("text.in","r",stdin);//文件忘记注释害人不浅！！ 
#endif
using namespace std;
map<int,int>m;
int a[100005],f[100005];
signed main(){
	int n,te;
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&te);
		m[te]=i;
	}
	for(int i=1;i<=n;i++){
		scanf("%d",&te);
		a[i]=m[te];
	}
	memset(f+1,0x3f,sizeof(int)*(n+1));
	int cnt=0;
	for(int i=1;i<=n;i++){
		int l=0,r=cnt,m=(l+r)/2;
		while(l<r){
			if(f[m]<a[i]&&f[m+1]>=a[i])break;
			if(f[m+1]<a[i])l=m+1;
			else r=m; 
			m=(l+r)/2;
		}
		f[m+1]=a[i];
		if(m==cnt)cnt++;
	}
	printf("%d",cnt);
	return 0;
}

4.字符串的修改

https://www.luogu.com.cn/problem/P2758

5.海盗分赃

http://acm.hdu.edu.cn/showproblem.php?pid=1538

6.The Uxuhul Voting System

http://acm.hnu.cn/online/?action=problem&type=show&id=10526&courseid=0

附加题：

1.Doing Homework HDU - 1074【状压dp】

http://acm.hdu.edu.cn/showproblem.php?pid=1074

#include<bits/stdc++.h>
#ifdef LOCAL
FILE*FP=freopen("text.in","r",stdin);
#endif
#define int long long 
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
char str[15][102];
int d[15],c[15],s[1<<15],p[1<<15];
int Day(int now){
	int sum=0,cnt=0;
	while(now){
		if(now&1)sum+=c[cnt];
		now>>=1;
		cnt++;
	}
	return sum;
}
void print(int num){
	if(num==0)return;
	print(num-(1<<p[num]));
	printf("%s\\n",str[p[num]]);
}
signed main(){
	int t;
	scanf("%d",&t);
	while(t--){
		int n;
		scanf("%d",&n);
		for(int i=0;i<n;i++){
			scanf("%s%d%d",str[i],&d[i],&c[i]);
		}
		s[0]=0;
		int num=(1<<n)-1;
		for(int i=1;i<=num;i++){
			s[i]=INF;
			int day=Day(i);
			for(int j=0;j<n;j++){
				if(!((i>>j)&1))continue;//再次提醒：！单目优先级高 
				int te=s[i-(1<<j)]+max(0LL,day-d[j]);
				if(te<=s[i]){
					s[i]=te;
					p[i]=j;
				}
			}
		}
		printf("%lld\\n",s[num]);
		print(num);
	}
	return 0;
}

2.hdu1024 max sum plus plus

http://acm.hdu.edu.cn/showproblem.php?pid=1024

#include<bits/stdc++.h>
using namespace std;
#define N 1000005
#define INF 0x3f3f3f3f
int a[N],s[N],p[N];
int t,m,n,ma;
int main(){
	while(~scanf("%d%d",&m,&n)){
		for(int i=1;i<=n;i++){
			scanf("%d",&a[i]);
		}
		memset(s,0,sizeof(int)*(n+2));
		memset(p,0,sizeof(int)*(n+2));
		for(int i=1;i<=m;i++){
			//ma=-INF;
			for(int j=i;j<=n;j++){
				s[j]=max(s[j-1],p[j-1])+a[j];
				if(j==i)p[j-1]=-INF,s[j-1]=-INF;
				else p[j-1]=max(p[j-2],s[j-1]);
				//p[j-1]=ma;//完成上行使命2333 
				//ma=max(ma,s[j]);//由于s[i-1]是可能更大的，所以要-INF 
			}
		}
		printf("%d\\n",*max_element(s+m,s+n+1));
	}
}

以上是关于ACM动态规划题的主要内容，如果未能解决你的问题，请参考以下文章

2018年暑假ACM个人训练题9（动态规划）解题报告

动态规划题 HDU-1024

ACM大神是怎么解决动态规划的？搞定DP看这就够了

ACM程序设计动态规划 第一篇 引入

DP动态规划-打ACM你必须知道的算法

ACM学习历程—SNNUOJ 1239 Counting Star Time(树状数组 && 动态规划 && 数论)