圆方树与仙人掌

Posted 2023-04-25 lsty

圆方树

前置知识：

1. 点双连通分量
2. tarjan 求点双

对于一个无向图，在维护某些信息时可以利用圆方树的方法把原图转为一棵树来处理

我们称在原图上的点是 圆点

对于每个点双联通分量，新建一个连向点双内所有点的新点，称其为 方点

点双内的所有点除了向 方点 连边以外不向点双内其他点连边，换句话说一个点双内，以方点为中心形成了一个菊花图的形状

来自WC的PPT(和小粉兔的博客)

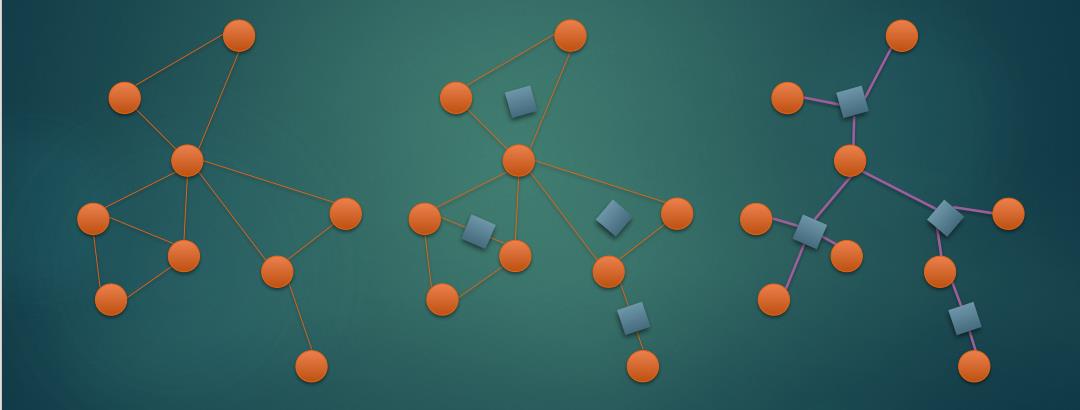
点双的数量 \\(<n\\)，所以圆方树的点数 \\(<2n\\)

显然如果原图有 \\(k\\) 个联通块，则原图会形成一个 \\(k\\) 棵树组成的森林

Tarjan 构造圆方树

利用 Tarjan 可以在求点双的同时顺便把圆方树建出来，在统计同一个点双里面的点的时候加一个向方点连边的过程即可

为了风格统一这里没有使用通常建圆方树时点入栈的方法，而是平时tarjan的边入栈

void dfs(int u, int fa) 
	low[u] = rnk[u] = ++dfc;
	int child = 0;
	for(int i : G[u]) 
		auto e = E[i];
		int v = e.v;
		if(!rnk[v]) 
			stk.push(e);
			dfs(v, u);
			low[u] = min(low[v], low[u]);
			child++;

			if(low[v] >= rnk[u]) 
				is_cut[u] = true;
				bcccnt++;

				while(1) 
					auto x = stk.top();
					stk.pop();
                    //建圆方树
					if(bccnu[x.u] != bcccnt)
						add2(x.u, n + bcccnt), bccnu[x.u] = bcccnt;
					if(bccnu[x.v] != bcccnt)
						add2(x.v, n + bcccnt), bccnu[x.v] = bcccnt;
					if(x == e)
						break;
				
			
		 else if(rnk[v] < rnk[u] && v != fa) 
			stk.push(e);
			low[u] = min(low[u], rnk[v]);
		
	
	if(fa == 0 && child == 1)
		is_cut[u] = 0;

inline void tarjan() 
	for(int u = 1; u <= n; u++)
		if(!rnk[u])
			dfs(u, 0);

圆方树的性质

1. 圆方树中圆点和方点交替出现

Example 1: UVA1464

给你一个 \\(n\\) 个点 \\(m\\) 条边的无向图，问从边 \\(S\\) 出发到边 \\(T\\) 无论怎么走都必须经过的点有几个

Solution

把圆方树建出来，答案就是 $u$ 和 $v$ 在树上简单路径上的圆点数量。
由于圆点和方点交替出现，分类讨论可以知道 $u$ 和 $v$ 之间圆点数量是 $(dep[u] + dep[v] - 2 * dep[lca]) / 2 - 1$

折叠代码块

 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

const int N = 1e4 + 10, M = 10 * N;
int n, m;

vector G[N], tr[N << 1];

int cnt;

struct edge 

int u, v;

edge() 

edge(int _u, int _v) 

u = _u, v = _v;



bool operator == (const edge& x) const 

return x.u == u && x.v == v;



E[M << 2], T[M << 2];
inline void add(int u, int v) 

E[cnt++] = edge(u, v);

E[cnt++] = edge(v, u);

G[u].push_back(cnt - 2);

G[v].push_back(cnt - 1);


int low[N], rnk[N], dfc;

int bccnu[N], is_cut[N], bcccnt;

int cnt2;
stack stk;
void add2(int u, int v) 

//printf("Add Edge: %d %d\\n", u, v);

T[cnt2++] = edge(u, v);

T[cnt2++] = edge(v, u);

tr[u].push_back(cnt2 - 2);

tr[v].push_back(cnt2 - 1);


void dfs(int u, int fa) 

low[u] = rnk[u] = ++dfc;

int child = 0;

for(int i : G[u]) 

auto e = E[i];

int v = e.v;

if(!rnk[v]) 

stk.push(e);

dfs(v, u);

low[u] = min(low[v], low[u]);

child++;
		if(low[v] >= rnk[u]) 
			is_cut[u] = true;
			bcccnt++;

			while(1) 
				auto x = stk.top();
				stk.pop();
				if(bccnu[x.u] != bcccnt)
					add2(x.u, n + bcccnt), bccnu[x.u] = bcccnt;
				if(bccnu[x.v] != bcccnt)
					add2(x.v, n + bcccnt), bccnu[x.v] = bcccnt;
				if(x == e)
					break;
			
		
	 else if(rnk[v] < rnk[u] && v != fa) 
		stk.push(e);
		low[u] = min(low[u], rnk[v]);
	

if(fa == 0 && child == 1)
	is_cut[u] = 0;



inline void tarjan() 

for(int u = 1; u <= n; u++)

if(!rnk[u])

dfs(u, 0);


int fa[21][N << 1];

int dep[N << 1];

void tree(int u, int f) 

fa[0][u] = f;

dep[u] = dep[f] + 1;
for(int i : tr[u]) 
	auto x = T[i];
	int v = x.v;
	if(v == f)
		continue;
	tree(v, u);



int LCA(int u, int v) 

if(dep[u] < dep[v])

swap(u, v);

for(int i = 20; i >= 0; i--)

if(dep[fa[i][u]] >= dep[v])

u = fa[i][u];

if(u == v)

return u;

for(int i = 20; i >= 0; i--) 

if(fa[i][u] != fa[i][v])

u = fa[i][u], v = fa[i][v];





u = fa[0][u];

return u;


inline void clear() 

for(int u = 1; u <= n; u++)

G[u].clear();

for(int u = 1; u <= n + bcccnt; u++)

tr[u].clear();

memset(is_cut, 0, (n + 1) * sizeof(int));

memset(bccnu, 0, (n + 1) * sizeof(int));

memset(low, 0, (n + 1) * sizeof(int));

memset(rnk, 0, (n + 1) * sizeof(int));

memset(fa, 0, sizeof(fa));

memset(dep, 0, sizeof(dep));

cnt = cnt2 = dfc = bcccnt = 0;


int calc(int u, int v) 

int lca = LCA(u, v);

return (dep[u] + dep[v] - 2 * dep[lca]) / 2 - 1;


int query(int u, int v) 

int a[2], b[2];

a[0] = E[(u - 1) * 2].u, a[1] = E[(u - 1) * 2].v;

b[0] = E[(v - 1) * 2].u, b[1] = E[(v - 1) * 2].v;

int ans = 0;

for(int i = 0; i < 2; i++)

for(int j = 0; j < 2; j++)

ans = max(ans, calc(a[i], b[j]));

return ans;


int main() 

//	freopen("input.txt", "r", stdin);

while(scanf("%d%d", &n, &m) == 2 && (n | m)) 

for(int i = 1; i <= m; i++) 

int u, v;

scanf("%d%d", &u, &v);

add(u, v);



tarjan();

for(int u = 1; u <= n + bcccnt; u++)

if(!dep[u])

tree(u, 0);

for(int k = 1; k < 21; k++)

for(int u = 1; u <= n + bcccnt; u++)

fa[k][u] = fa[k-1][fa[k-1][u]];
	int Q;
	scanf("%d", &Q);
	for(int i = 1; i <= Q; i++) 
		int u, v;
		scanf("%d%d", &u, &v);

		printf("%d\\n", query(u, v));
	
	clear();

return 0;

例题

仙人掌上圆方树

圆方树总结

• 圆方树：一种将由图转化而成的树，从而大大了增加题目的可解性，且大多广泛用于仙人掌图中。

• 针对仙人掌图上的圆方树：仙人掌是指一条边至多只被一个环包含的无向图。

• 树上的点：圆方树上分为两类点，一类是圆点，一类是方点。圆点即原图中所有的点，方点即为了去环而新添加进去的，满足一定性质的点。

• 构造思路：圆圆边直接加入，对于仙人掌中的任意一个环，每个环上的点在圆方树上对应的圆点向这个环对应的方点连边，方点为一个新建节点。

• 环的根：指定一个圆点为圆方树的根，把方点的父亲叫做这个方点对应的环的根。

• 圆方边边权：若一个在环上的圆点不是环的根，它到对应方点的边权为到环的根的最短距离，环的根到环所对应的方点的边权为零。

解题：

• 多数是为了可以用树上的算法，例如倍增、树剖解决问题，以两点间路径的问题为例：

• 若 \(lca\) 是圆点，那么答案就是路径上的贡献；

• 若 \(lca\) 是方点，则找到进入这个环的两个点，这两个点之间的有两条路径，选择合题意的一条加入贡献。

• 在树链剖分中，进入一个环的两个点有两种情况：一是一个为 \(dfs\) 序比 \(lca\) 大 \(1\) 的点，即 \(lca\) 所在重链上的儿子，另一个为最后经过的 \(top\)；二是最后经过的两个 \(top\)。

洛谷模板题：

#include <cmath>
#include <queue>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int maxn = 40000 + 10;
int n, m, q, head_g[maxn], head_t[maxn], st[17][maxn], edge_num_g, edge_num_t, dfn_num, col_num, top;
int dfn[maxn], low[maxn], sta[maxn];
long long deep[maxn], dis[maxn], sum[maxn], sccsum[maxn];

struct Edge  int v, nxt; long long w;  edge_g[maxn << 2], edge_t[maxn << 2];

inline void Add_edge_g(int u, int v, long long w) 
  edge_g[++edge_num_g].v = v, edge_g[edge_num_g].w = w, edge_g[edge_num_g].nxt = head_g[u], head_g[u] = edge_num_g;


inline void Add_edge_t(int u, int v, long long w) 
  edge_t[++edge_num_t].v = v, edge_t[edge_num_t].w = w, edge_t[edge_num_t].nxt = head_t[u], head_t[u] = edge_num_t;


inline void Tarjan(int x, int p) 
  dfn[x] = low[x] = ++dfn_num, sta[++top] = x;
  for(int i = head_g[x]; i; i = edge_g[i].nxt) if( edge_g[i].v != p ) 
    if( dfn[edge_g[i].v] == 0 ) 
      sum[edge_g[i].v] = sum[x] + edge_g[i].w, Tarjan(edge_g[i].v, x), low[x] = min(low[x], low[edge_g[i].v]);
      if( low[edge_g[i].v] > dfn[x] ) Add_edge_t(x, edge_g[i].v, edge_g[i].w), Add_edge_t(edge_g[i].v, x, edge_g[i].w);  // 树边，圆圆边加入
    
    else if( dfn[edge_g[i].v] < low[x] )   // 返祖边，得环，建立方点及圆方边
      sccsum[++col_num] = sum[x] - sum[edge_g[i].v] + edge_g[i].w;  // 得环长，col_num 认为是方点编号
      for(int j = top; sta[j] != edge_g[i].v; --j) 
        int _w = min(sum[sta[j]] - sum[edge_g[i].v], sccsum[col_num] - sum[sta[j]] + sum[edge_g[i].v]); // 到此环的根的距离，即圆方边边权
        Add_edge_t(n + col_num, sta[j], _w), Add_edge_t(sta[j], n + col_num, _w);
      
      Add_edge_t(n + col_num, edge_g[i].v, 0), Add_edge_t(edge_g[i].v, n + col_num, 0); // 环的根所对应的圆方边权为 0
      low[x] = dfn[edge_g[i].v];
    
  
  --top;


inline void Deep_fs(int x, int p) 
  for(int i = 1; i < 17; ++i) st[i][x] = st[i - 1][st[i - 1][x]];
  for(int i = head_t[x]; i; i = edge_t[i].nxt) if( edge_t[i].v != p ) 
    st[0][edge_t[i].v] = x;
    dis[edge_t[i].v] = dis[x] + edge_t[i].w, deep[edge_t[i].v] = deep[x] + 1, Deep_fs(edge_t[i].v, x);
  


inline long long Querry(int x, int y) 
  int lca = 0, res = dis[x] + dis[y];
  if( deep[x] < deep[y] ) swap(x, y);
  for(int i = 16; i >= 0; --i) if( deep[st[i][x]] >= deep[y] ) x = st[i][x];
  if( x == y ) lca = x;
  else 
    for(int i = 16; i >= 0; --i) if( st[i][x] != st[i][y] ) x = st[i][x], y = st[i][y];
    lca = st[0][x];
  
  if( lca <= n ) return res - (dis[lca] << 1);
  if( dfn[x] > dfn[y] ) swap(x, y);
  return res - dis[x] - dis[y] + min(sum[y] - sum[x], sccsum[lca - n] - sum[y] + sum[x]);


int main(int argc, char const *argv[])

  scanf("%d%d%d", &n, &m, &q);
  for(int u, v, w, i = 1; i <= m; ++i) scanf("%d%d%d", &u, &v, &w), Add_edge_g(u, v, w), Add_edge_g(v, u, w);
  deep[1] = 1, Tarjan(1, 0), Deep_fs(1, 0);
  for(int u, v, i = 1; i <= q; ++i) scanf("%d%d", &u, &v), printf("%lld\n", Querry(u, v));

  return 0;