第14届蓝桥杯C++B组省赛题解(A-J)(更新完毕)
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第14届蓝桥杯C++B组省赛题解(A-J)(更新完毕)相关的知识,希望对你有一定的参考价值。
A. 日期统计
题目内容
小蓝现在有一个长度为 \\(100\\) 的数组,数组中的每个元素的值都在 \\(0\\) 到 \\(9\\) 的范围之内。
数组中的元素从左至右如下所示:
5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 2 7
0 5 8 8 5 7 0 9 9 1 9 4 4 6 8 6 3 3 8 5 1 6 3 4 6 7 0 7 8 2 7 6 8 9 5 6 5 6 1 4 0 1
0 0 9 4 8 0 9 1 2 8 5 0 2 5 3 3
现在他想要从这个数组中寻找一些满足以下条件的子序列:
- 子序列的长度为 \\(8\\);
- 这个子序列可以按照下标顺序组成一个 \\(yyyymmdd\\) 格式的日期,并且
要求这个日期是 \\(2023\\) 年中的某一天的日期,例如 \\(20230902,20231223\\)。
\\(yyyy\\) 表示年份,\\(mm\\) 表示月份,\\(dd\\) 表示天数,当月份或者天数的长度只有一位时需要一个前导零补充。
请你帮小蓝计算下按上述条件一共能找到多少个不同的 \\(2023\\) 年的日期。
对于相同的日期你只需要统计一次即可。
本题的结果为一个整数,在提交答案时只输出这个整数,输出多余的内容将无法得分。
思路
八重循环枚举日期+set去重即可
\\(Tips:\\) 前4重特判2023,否则程序会跑的很慢
代码
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n=100;
int num[N];
set<string>s;
bool check(string all)
int m=stoi(all.substr(0,2));
int d=stoi(all.substr(2,2));
int mon[]=0,31,28,31,30,31,30,31,31,30,31,30,31;
if(m>=1&&m<=12)
if(d>=1&&d<=mon[m])
return true;
return false;
int main()
for(int i=0;i<n;i++)cin>>num[i];
for(int a=0;a<n;a++)
if(num[a]!=2)continue;
for(int b=a+1;b<n;b++)
if(num[b]!=0)continue;
for(int c=b+1;c<n;c++)
if(num[c]!=2)continue;
for(int d=c+1;d<n;d++)
if(num[d]!=3)continue;
for(int e=d+1;e<n;e++)
for(int f=e+1;f<n;f++)
for(int g=f+1;g<n;g++)
for(int h=g+1;h<n;h++)
string n1=to_string(num[e]);
string n2=to_string(num[f]);
string n3=to_string(num[g]);
string n4=to_string(num[h]);
string all=n1+n2+n3+n4;
if(check(all))s.insert(all);
cout<<s.size()<<endl;
return 0;
答案
235
B.01 串的熵
题目内容
对于一个长度 $ n $ 的 \\(01\\) 串 \\(S = x_1x_2x_3...x_n\\)。
香农信息熵的定义为:\\(H(S)=-\\sum_i=1^np(x_i)log_2(p(x_i))\\) ,其中 \\(p(0)\\), \\(p(1)\\) 表示在这个 \\(01\\) 串中 \\(0\\) 和 \\(1\\) 出现的占比。
比如,对于 \\(S = 100\\) 来说,信息熵 \\(H(S) = - \\frac13log_2(\\frac13) - \\frac23 log_2(\\frac23) = 1.3083\\)。
对于一个长度为 \\(23333333\\) 的 \\(01\\) 串,如果其信息熵为 \\(11625907.5798\\) ,且 \\(0\\) 出现次数比 \\(1\\) 少,那么这个 \\(01\\) 串中 \\(0\\) 出现了多少次?
本题的结果为一个整数,在提交答案时只输出这个整数,输出多余的内容将无法得分。
思路
按题意模拟即可,由题意可得 \\(H(S)\\)的值只与 \\(01\\) 出现的次数有关,因为 \\(0\\) 出现次数比 \\(1\\) 少,所以可以从 \\(\\lfloor \\frac233333332 \\rfloor = 11666666\\) 开始往下枚举0的个数,同时计算 \\(p(0),p(1)\\) 的占比,带入公式验证是否相等,注意设置误差范围去判断浮点数是否相等
代码
#include<bits/stdc++.h>
using namespace std;
const double eps=1e-4;
//#define double long double
int len;
int main()
int len=23333333;
for(int i=len/2;i>=1;i--)
double px0=1.0*i/len,px1=1.0*(len-i)/len;
double H=-(i*px0*log2(px0)+(len-i)*px1*log2(px1));
if(fabs(H-11625907.5798)<=eps)
cout<<i<<endl;
return 0;
return 0;
答案
11027421
C.冶炼金属
题目内容
小蓝有一个神奇的炉子用于将普通金属 \\(O\\) 冶炼成为一种特殊金属 \\(X\\) 。这个炉子有一个称作转换率的属性 \\(V\\) ,\\(V\\) 是一个正整数,这意味着消耗 \\(V\\) 个普通金属 \\(O\\) 恰好可以冶炼出一个特殊金属 \\(X\\)。当普通金属 \\(O\\) 的数目不足 \\(V\\) 时,无法继续冶炼。现在给出了 \\(N\\) 条冶炼记录,每条记录中包含两个整数 \\(A\\) 和 \\(B\\),这表示本次投入了 \\(A\\) 个普通金属\\(O\\),最终冶炼出了 \\(B\\) 个特殊金属 \\(X\\)。每条记录都是独立的,这意味着上一次没消耗完的普通金属 \\(O\\) 不会累加到下一次的冶炼当中。根据这 \\(N\\) 条冶炼记录,请你推测出转换率 \\(V\\) 的最小值和最大值分别可能是多少。题目保证评测数据不存在无解的情况。
输入格式
第一行一个整数 \\(N\\),表示冶炼记录的数目。
接下来输入 \\(N\\) 行,每行两个整数 \\(A、B\\) ,含义如题目所述。
对于 \\(30\\%\\) 的评测用例,\\(1 ≤ N ≤ 100\\)
对于 \\(60\\%\\) 的评测用例,\\(1 ≤ N ≤ 1000\\)
对于 \\(100\\%\\) 的评测用例,\\(1 ≤ N ≤ 10000,1 ≤ B ≤ A ≤ 1,000,000,000\\)
输出格式
输出两个整数,分别表示 \\(V\\) 可能的最小值和最大值,中间用空格分开。
输入样例
3
75 3
53 2
59 2
输出样例
20 25
思路
求最小值和最大值问题,可以利用二分答案进行判断。
-
求最小值
- 假设最终答案为 \\(S\\)
- 因为 \\(S\\) 的最优性,若要求答案 \\(<S\\),对于每组金属 \\(A\\) 至少有一个不能冶炼出 \\(B\\) 个特殊金属
- 若答案可以 \\(>S\\),则一定存在一个属性 \\(V\\) ,使得每组金属 \\(A\\) 都能冶炼出对应的 \\(B\\) 个特殊金属,最优解就处于可行性的分界点上
- 假设最终答案为 \\(S\\)
-
求最大值与上面同理
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
int a[N],b[N];
int n;
bool check_min(int x)
//如果某一组存在a[i]/x的值比实际B大,说明V可以继续增加
for(int i=0;i<n;i++)
if(a[i]/x>b[i])return false;
return true;
bool check_max(int x)
//如果某一组存在a[i]/x的值比实际B小,说明V可以继续减小
for(int i=0;i<n;i++)
if(a[i]/x<b[i])return false;
return true;
int main()
cin>>n;
for(int i=0;i<n;i++)cin>>a[i]>>b[i];
int l=0,r=1e9;
//求最小值
while(l<r)
int mid=l+r>>1;
if(check_min(mid))r=mid;
else l=mid+1;
cout<<l<<\' \';
l=0,r=1e9;
//求最大值
while(l<r)
int mid=l+r+1>>1;
//
if(check_max(mid))l=mid;
else r=mid-1;
cout<<l<<endl;
return 0;
D.飞机降落
题目内容
\\(N\\) 架飞机准备降落到某个只有一条跑道的机场,其中第 \\(i\\) 架飞机在 \\(T_i\\) 时刻到达机场上空,到达时它的剩余油料还可以继续盘旋 \\(D_i\\) 个单位时间。即它最早可以于 \\(T_i\\) 时刻开始降落,最晚可以于 \\(T_i + D_i\\) 时刻开始降落。降落过程需要 \\(L_i\\) 个单位时间。一架飞机降落完毕时,另一架飞机可以立即在同一时刻开始降落。但是不能在前一架飞机完成降落前开始降落。请你判断 \\(N\\) 架飞机是否可以全部安全降落。
输入格式
输入包含多组数据。
第一行包含一个整数 \\(T\\) ,代表测试数据的组数。
对于每组数据,第一行包含一个整数 \\(N\\) 。
以下 \\(N\\) 行,每行包含三个整数:\\(T_i,D_i\\) 和 \\(L_i\\)
对于 \\(30\\%\\) 的数据,\\(N ≤ 2\\)
对于 \\(100\\%\\) 的数据,\\(1 ≤ T ≤ 10,1 ≤ N ≤ 10,0 ≤ T_i,D_i,L_i ≤ 100,000\\)
输出格式
对于每组数据,输出 \\(YES\\) 或者 \\(NO\\),代表是否可以全部安全降落。
输入样例
2
3
0 100 10
10 10 10
0 2 20
3
0 10 20
10 10 20
20 10 20
输出样例
YES
NO
对于第一组数据:
安排第 \\(3\\) 架飞机于 \\(0\\) 时刻开始降落,\\(20\\) 时刻完成降落。
安排第 \\(2\\) 架飞机于 \\(20\\) 时刻开始降落,\\(30\\) 时刻完成降落。
安排第 \\(1\\) 架飞机于 \\(30\\) 时刻开始降落,\\(40\\) 时刻完成降落。
对于第二组数据,无论如何安排,都会有飞机不能及时降落。
思路
\\(N\\)最大只有\\(10\\),最多10组测试组数,可以暴搜枚举所有方案
- 优化:若搜索到一种合法方案,剪枝一路返回即可,不需要继续搜索
代码
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int>PII;
const int N=12;
PII a[N];
int d[N];
bool st[N];
int n;
//代表枚举到第u层,当前飞机的降落结束时间为now
bool dfs(int u,int now)
if(u>=n)
for(int i=0;i<n;i++)
if(!st[i])return false;
return true;
for(int i=0;i<n;i++)
if(!st[i])
st[i]=true;
//如果当前飞机的最早降落时间小于等于now,并且最晚降落时间大于等于now,
//则从当前时刻开始降落
if(a[i].x<=now&&a[i].y>=now)
//降落结束时间now更新为now+d[i],继续枚举下一架飞机
if(dfs(u+1,now+d[i]))return true;
//如果当前飞机的最早降落时间大于等于now
else if(a[i].x>=now)
//降落结束时间now更新为a[i].x+d[i],继续枚举下一架飞机
if(dfs(u+1,a[i].x+d[i]))return true;
st[i]=false;
return false;
int main()
int T;
cin>>T;
while(T--)
cin>>n;
for(int i=0;i<n;i++)
cin>>a[i].x>>a[i].y>>d[i];
a[i].y+=a[i].x;
memset(st,0,sizeof st);
puts(dfs(0,0)?"YES":"NO");
return 0;
E.接龙数列
题目内容
对于一个长度为 \\(K\\) 的整数数列:\\(A_1, A_2, ... , A_K\\),我们称之为接龙数列:当且仅当 \\(A_i\\) 的首位数字恰好等于 \\(A_i−1\\) 的末位数字\\((2 ≤ i ≤ K)\\)。例如:\\(12, 23, 35, 56, 61, 11\\) 是接龙数列;\\(12, 23, 34, 56\\) 不是接龙数列,因为 \\(56\\) 的首位数字不等于 \\(34\\) 的末位数字。所有长度为 1 的整数数列都是接龙数列。现在给定一个长度为 \\(N\\) 的数列 \\(A_1, A_2, ... , A_N\\),请你计算最少从中删除多少个数,可以使剩下的序列是接龙序列?
输入格式
第一行包含一个整数 \\(N\\) 。
第二行包含 \\(N\\) 个整数 \\(A_1, A_2, ... , A_N\\)。
对于 \\(20\\%\\) 的数据,\\(1 ≤ N ≤ 20\\)。
对于 \\(50\\%\\) 的数据,\\(1 ≤ N ≤ 10000\\)。
对于 \\(100\\%\\) 的数据,\\(1 ≤ N ≤ 10^5,1 ≤ A_i ≤ 10^9\\)。
所有 \\(A_i\\) 保证不包含前导 \\(0\\)。
输出格式
一个整数代表答案。
输入样例
5
11 121 22 12 2023
输出样例
1
删除 \\(22\\),剩余 $ 11, 121, 12, 2023 $ 是接龙数列。
思路
线性 \\(dp\\),定义状态 \\(f[i]\\) , 代表以 \\(i\\) 结尾的最长序列的长度
因此,所求的最少删除数的个数 = $n - $最长接龙序列的长度
代码
#include<bits/stdc++.h>
using namespace std;
const int N=12;
int f[N];
int main()
int n;
cin>>n;
int maxv=0;
for(int i=0;i<n;i++)
string s;
cin>>s;
int a=s[0]-\'0\',b=s.back()-\'0\';
f[b]=max(f[b],f[a]+1);//接到前面以a结尾的数后面;或者替换掉前面一个以b结尾的数,保持不变
maxv=max(maxv,f[b]);//更新最大值
cout<<n-maxv<<endl;
return 0;
F.岛屿数量
题目内容
小蓝得到了一副大小为 \\(M × N\\) 的格子地图,可以将其视作一个只包含字符\\(0\\)(代表海水)和 \\(1\\)(代表陆地)的二维数组,地图之外可以视作全部是海水,每个岛屿由在上/下/左/右四个方向上相邻的 \\(1\\) 相连接而形成。在岛屿 A 所占据的格子中,如果可以从中选出 \\(k\\) 个不同的格子,使得他们的坐标能够组成一个这样的排列:\\((x_0, y_0),(x_1, y_1), . . . ,(x_k−1, y_k−1)\\),其中 \\((\\) \\(x_(i+1)\\%k, y_(i+1)\\%k\\) \\()\\) 是由 \\((x_i, y_i)\\) 通过上/下/左/右移动一次得来的 \\((0 ≤ i ≤ k − 1)\\),此时这 \\(k\\) 个格子就构成了一个 “环”。如果另一个岛屿 \\(B\\) 所占据的格子全部位于这个 “环” 内部,此时我们将岛屿 B 视作是岛屿 \\(A\\) 的子岛屿。若 \\(B\\) 是 \\(A\\) 的子岛屿,\\(C\\) 又是 \\(B\\) 的子岛屿,那 \\(C\\) 也是 \\(A\\) 的子岛屿。请问这个地图上共有多少个岛屿?在进行统计时不需要统计子岛屿的数目。
输入格式
第一行一个整数 \\(T\\),表示有 \\(T\\) 组测试数据。
接下来输入 \\(T\\) 组数据。对于每组数据,第一行包含两个用空格分隔的整数 \\(M、N\\) 表示地图大小;接下来输入 \\(M\\) 行,每行包含 \\(N\\) 个字符,字符只可能是 \\(0\\) 或 \\(1\\)
输出格式
对于每组数据,输出一行,包含一个整数表示答案。
输入样例
2
5 5
01111
11001
10101
10001
11111
5 6
111111
100001
010101
100001
111111
输出样例
1
3
对于第一组数据,包含两个岛屿,下面用不同的数字进行了区分:
01111
11001
10201
10001
11111
岛屿 \\(2\\) 在岛屿 \\(1\\) 的 “环” 内部,所以岛屿 \\(2\\) 是岛屿 \\(1\\) 的子岛屿,答案为 \\(1\\)。
对于第二组数据,包含三个岛屿,下面用不同的数字进行了区分:
111111
100001
020301
100001
111111
注意岛屿 \\(3\\) 并不是岛屿 \\(1\\) 或者岛屿 \\(2\\) 的子岛屿,因为岛屿 \\(1\\) 和岛屿 \\(2\\) 中均没有“环”。
对于 \\(30\\%\\) 的评测用例,\\(1 ≤ M, N ≤ 10\\) 。
对于 \\(100\\%\\) 的评测用例,\\(1 ≤ T ≤ 10,1 ≤ M, N ≤ 50\\) 。
思路
两次宽搜,从 \\((1,1)\\) 处存图
- 第一次宽搜,先从 \\((0,0)\\) ,即海水处开始向八个方向搜索,将能搜索到的 \\(0\\) 标记成 \\(\\#\\),将每块岛屿分隔开
- 第二次宽搜,遍历 \\(g[][]\\) 数组,当遇到 \\(1\\) 的时候,将 \\(1\\) 包围的整块区域标记成 \\(\\#\\),同时要统计的岛屿个数加一
代码
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int,int>PII;
const int N=55;
char g[N][N];
int n,m;
int dx[]=-1,0,1,0,-1,-1,1,1;
int dy[]=0,1,0,-1,-1,1,1,-1;
//分隔岛屿
void bfs1(int x,int y)
queue<PII>q;
q.push(0,0);
g[0][0]=\'#\';
while(q.size())
auto t=q.front();
q.pop();
for(int i=0;i<8;i++)
int a=t.x+dx[i],b=t.y+dy[i];
if(a<0||a>n+1||b<0||b>m+1||g[a][b]==\'1\'||g[a][b]==\'#\')continue;
g[a][b]=\'#\';
q.push(a,b);
//将整块岛屿标记
void bfs2(int x,int y)
queue<PII>q;
q.push(x,y);
g[x][y]=\'#\';
while(q.size())
auto t=q.front();
q.pop();
for(int i=0;i<4;i++)
int a=t.x+dx[i],b=t.y+dy[i];
if(a<1||a>n||b<1||b>m||g[a][b]==\'#\')continue;
g[a][b]=\'#\';
q.push(a,b);
int main()
int T;
cin>>T;
while(T--)
cin>>n>>m;
memset(g,\'0\',sizeof g);
for(int i=1;i<=n;i++)cin>>g[i]+1;
int x,y;
bfs1(x,y);
int cnt=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(g[i][j]==\'1\')
bfs2(i,j),cnt++;//统计个数
cout<<cnt<<endl;
return 0;
G.子串简写
题目内容
程序猿圈子里正在流行一种很新的简写方法:
对于一个字符串,只保留首尾字符,将首尾字符之间的所有字符用这部分的长度代替。
例如 \\(internationalization\\) 简写成 \\(i18n,Kubernetes\\) 简写成 \\(K8s, Lanqiao\\) 简写成 \\(L5o\\) 等。
在本题中,我们规定长度大于等于 \\(K\\) 的字符串都可以采用这种简写方法。
长度小于 \\(K\\) 的字符串不允许使用这种简写。
给定一个字符串 \\(S\\) 和两个字符 \\(c_1\\) 和 \\(c_2\\)。
请你计算 \\(S\\) 有多少个以 \\(c_1\\) 开头 \\(c_2\\) 结尾的子串可以采用这种简写?
输入格式
第一行包含一个整数 \\(K\\)。
第二行包含一个字符串 \\(S\\) 和两个字符 \\(c_1\\) 和 \\(c_2\\)。
对于 \\(20\\%\\) 的数据,\\(2 ≤ K ≤ |S| ≤ 10000\\)。
对于 \\(100\\%\\) 的数据,\\(2 ≤ K ≤ |S| ≤ 5 × 10^5\\)。
\\(S\\) 只包含小写字母。\\(c_1\\) 和 \\(c_2\\) 都是小写字母。
\\(|S|\\) 代表字符串 \\(S\\) 的长度。
输出格式
一个整数代表答案
输入样例
4
abababdb a b
输出样例
6
符合条件的子串如下所示,中括号内是该子串:
\\([abab]abdb\\)
\\([ababab]db\\)
\\([abababdb]\\)
\\(ab[abab]db\\)
\\(ab[ababdb]\\)
\\(abab[abdb]\\)
思路
先求出 \\(c_1\\) 的前缀和数组 \\(s[i]\\) ,统计\\(c_1\\)在前缀中出现的次数。接着遍历字符串,每遇到一次 \\(c_2\\) ,就加上 \\(s[i-k+1]\\) ,即加上以 \\(c_1\\) 开头 \\(c_2\\) 结尾且长度大于等于 \\(K\\) 的字符串,最后得到答案。
\\(Tips:\\)注意最后答案可能很大,要开 \\(longlong\\)
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=5e5+10;
char str[N];
ll cnt[N];
char st,ed;
int k;
int main()
cin>>k;
cin>>str+1>>st>>ed;
int n=strlen(str+1);
//统计c1的前缀和
for(int i=1;i<=n;i++)
if(str[i]==st)cnt[i]=cnt[i-1]+1;
else cnt[i]=cnt[i-1];
//累加求个数
ll res=0;
for(int i=k;i<=n;i++)
if(str[i]==ed)res+=cnt[i-k+1];
cout<<res<<endl;
return 0;
H.整数删除
题目内容
给定一个长度为 \\(N\\) 的整数数列:\\(A_1, A_2, . . . , A_N\\) 。你要重复以下操作 \\(K\\) 次:
每次选择数列中最小的整数(如果最小值不止一个,选择最靠前的),将其删除。并把与它相邻的整数加上被删除的数值。输出 \\(K\\) 次操作后的序列。
输入格式
第一行包含两个整数 \\(N\\) 和 \\(K\\)。
第二行包含 \\(N\\) 个整数,\\(A_1, A_2, A_3, . . . , A_N\\)。
输出格式
输出 \\(N − K\\) 个整数,中间用一个空格隔开,代表 \\(K\\) 次操作后的序列。
输入样例
5 3
1 4 2 8 7
输出样例
17 7
数列变化如下,中括号里的数是当次操作中被选择的数:
[1] 4 2 8 7
5 [2] 8 7
[7] 10 7
17 7
对于 \\(20\\%\\) 的数据,\\(1 ≤ K < N ≤ 10000\\)。
对于 \\(100\\%\\) 的数据,\\(1 ≤ K < N ≤ 5 × 10^5,0 ≤ A_i ≤ 10^8\\)。
思路
题目关键是删除数列最小值,并且动态维护最小值。若取出最小元素的值比原来有变化,要重新放入优先队列中判断;否则就将其删除
- 删除操作考虑使用双链表,进行 \\(O(1)\\) 删除
- 最小值利用优先队列去维护
代码
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
const int N=5e5+10;
typedef long long ll;
typedef pair<ll,int>PII;
ll e[N],l[N],r[N];
priority_queue<PII,vector<PII>,greater<PII>>q;
int n,k;
//双链表删除
void dele(int k)
l[r[k]]=l[k];
r[l[k]]=r[k];
e[l[k]]+=e[k];
e[r[k]]+=e[k];
int main()
cin>>n>>k;
//双链表的头尾
r[0]=1,l[n+1]=n;
for(int i=1;i<=n;i++)
int x;
cin>>x;
e[i]=x,l[i]=i-1,r[i]=i+1;
q.push(e[i],i);//优先队列,小根堆,储存值和编号
while(k--)
auto t=q.top();
q.pop();
//取出最小元素,如果值有变化,重新放入优先队列中;否则将其删除
if(t.x!=e[t.y])q.push(e[t.y],t.y),k++;
else dele(t.y);
for(int i=r[0];i!=n+1;i=r[i])
cout<<e[i]<<\' \';
return 0;
I.景区导游
题目内容
某景区一共有 \\(N\\) 个景点,编号 \\(1\\) 到 \\(N\\)。景点之间共有 \\(N − 1\\) 条双向的摆渡车线路相连,形成一棵树状结构。在景点之间往返只能通过这些摆渡车进行,需要花费一定的时间。
小明是这个景区的资深导游,他每天都要按固定顺序带客人游览其中 \\(K\\) 个景点:\\(A_1, A_2, . . . , A_K\\) 。今天由于时间原因,小明决定跳过其中一个景点,只带游客按顺序游览其中 \\(K − 1\\) 个景点。具体来说,如果小明选择跳过 \\(A_i\\),那么他会按顺序带游客游览 $ A_1, A_2, . . . , A_i−1, A_i+1, . . . , A_K, (1 ≤ i ≤ K) $。
请你对任意一个 \\(A_i\\),计算如果跳过这个景点,小明需要花费多少时间在景点之间的摆渡车上?
输入格式
第一行包含 \\(2\\) 个整数 \\(N\\) 和 \\(K\\)。
以下 \\(N − 1\\) 行,每行包含 \\(3\\) 个整数 \\(u, v\\) 和 \\(t\\),代表景点 \\(u\\) 和 \\(v\\) 之间有摆渡车线路,花费 \\(t\\) 个单位时间。
最后一行包含 \\(K\\) 个整数 \\(A_1, A_2, . . . , A_K\\) 代表原定游览线路。
输出格式
输出 \\(K\\) 个整数,其中第 \\(i\\) 个代表跳过 \\(A_i\\) 之后,花费在摆渡车上的时间。
输入样例
6 4
1 2 1
1 3 1
3 4 2
3 5 2
4 6 3
2 6 5 1
输出样例
10 7 13 14
原路线是 \\(2 → 6 → 5 → 1\\)。
当跳过 \\(2\\) 时,路线是 \\(6 → 5 → 1\\),其中 \\(6 → 5\\) 花费时间 \\(3 + 2 + 2 = 7,5 → 1\\) 花费时间 \\(2 + 1 = 3\\),总时间花费 \\(10\\)。
当跳过 \\(6\\) 时,路线是 \\(2 → 5 → 1\\),其中 \\(2 → 5\\) 花费时间 \\(1 + 1 + 2 = 4,5 → 1\\) 花费时间 \\(2 + 1 = 3\\),总时间花费 \\(7\\)。
当跳过 \\(5\\) 时,路线是 \\(2 → 6 → 1\\),其中 \\(2 → 6\\) 花费时间 \\(1 + 1 + 2 + 3 = 7,6 → 1\\) 花费时间 \\(3 + 2 + 1 = 6\\),总时间花费 \\(13\\)。
当跳过 $1 $时,路线时 \\(2 → 6 → 5\\),其中 \\(2 → 6\\) 花费时间 \\(1 + 1 + 2 + 3 = 7,6 → 5\\) 花费时间 \\(3 + 2 + 2 = 7\\),总时间花费 \\(14\\)。
对于 \\(20\\%\\) 的数据,\\(2 ≤ K ≤ N ≤ 10^2\\)。
对于 \\(40\\%\\) 的数据,\\(2 ≤ K ≤ N ≤ 10^4\\)。
对于 \\(100\\%\\) 的数据,\\(2 ≤ K ≤ N ≤ 10^5,1 ≤ u, v, A_i ≤ N,1 ≤ t ≤ 10^5\\)。保证 \\(A_i\\) 两两不同。
思路
\\(LCA\\)板子题,题目中是一棵树形图,求用时即为求树上任意两点间的距离,可利用\\(LCA\\)快速求出两点之间的距离。求树上两个点距离的时候,可以预处理出每个点到根节点的距离。
两点间最短距离公式: \\(x\\) 到 \\(y\\) 的距离 \\(= d[x]+d[y] - 2*d[lca(x,y)]\\) ,本题可以先计算不跳过景点时的总用时,之后分类讨论
- 删除第 \\(1\\) 个结点时,减去 \\(1 \\sim 2\\) 之间的用时即可
- 删除第 \\(k\\) 个结点时,减去 \\(k-1 \\sim k\\) 之间的用时
- 其他情况减去 \\(i-1 \\sim i,i\\sim i+1\\) 之间的用时,并且加上 \\(i-1 \\sim i+1\\) 之间的用时
时间复杂度:预处理 \\(O(nlogn)\\) 查询:\\(O(logn)\\)
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,M=N*2;
typedef long long ll;
int h[N],e[M],ne[M],w[M],idx;
int f[N][20];
int depth[N];
ll d[N];
int A[N];
void add(int a,int b,int c)
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
//计算所有结点到根节点1的距离
void bfs()
queue<int>q;
depth[1]=1;
q.push(1);
while(q.size())
int t=q.front();
q.pop();
for(int i=h[t];i!=-1;i=ne[i])
int j=e[i];
if(depth[j])continue;
q.push(j);
if(depth[j])continue;
depth[j]=depth[t]+1;
d[j]=d[t]+w[i];
f[j][0]=t;
for(int k=1;k<=19;k++)
f[j][k]=f[f[j][k-1]][k-1];
//倍增法求lca
int lca(int a,int b)
if(depth[a]<depth[b])swap(a,b);
for(int i=19;i>=0;i--)
if(depth[f[a][i]]>=depth[b])
a=f[a][i];
if(a==b)return a;
for(int i=19;i>=0;i--)
if(f[a][i]!=f[b][i])
a=f[a][i],b=f[b][i];
return f[a][0];
int main()
memset(h,-1,sizeof h);
int n,k;
cin>>n>>k;
for(int i=0;i<n-1;i++)
int a,b,c;
cin>>a>>b>>c;
add(a,b,c),add(b,a,c);
bfs();
for(int i=1;i<=k;i++)
cin>>A[i];
//求不删除结点前的总用时
ll res=0;
for(int i=2;i<=k;i++)
int p=lca(A[i],A[i-1]);
res+=d[A[i]]+d[A[i-1]]-2*d[p];
for(int i=1;i<=k;i++)
ll dist;
if(i==1)//删除第一个结点时,减去1~2之间的用时即可
int p=lca(A[1],A[2]);
dist=d[A[1]]+d[A[2]]-2*d[p];
cout<<res-dist<<\' \';
else if(i==k)//删除第k个结点时,减去k-1~k之间的用时
int p=lca(A[k],A[k-1]);
dist=d[A[k]]+d[A[k-1]]-2*d[p];
cout<<res-dist<<\' \';
else//其他情况减去i-1~i,i~i+1之间的用时,并且加上i-1~i+1之间的用时
int p1=lca(A[i-1],A[i]);
int p2=lca(A[i],A[i+1]);
int p3=lca(A[i-1],A[i+1]);
dist=d[A[i-1]]+d[A[i]]-2*d[p1]+d[A[i]]+d[A[i+1]]-2*d[p2];
cout<<res-dist+d[A[i-1]]+d[A[i+1]]-2*d[p3]<<\' \';
return 0;
J.砍树
题目内容
题目描述
给定一棵由 \\(n\\) 个结点组成的树以及 \\(m\\) 个不重复的无序数对 $(a_1, b_1), (a_2, b_2), ... , (a_m, b_m) $,其中 \\(a_i\\) 互不相同,\\(b_i\\) 互不相同,\\(a_i ≠ b_j(1 ≤ i, j ≤ m)\\)。
小明想知道是否能够选择一条树上的边砍断,使得对于每个 \\((a_i, b_i)\\) 满足 \\(a_i\\) 和 \\(b_i\\) 不连通。
如果可以则输出应该断掉的边的编号(编号按输入顺序从 \\(1\\) 开始),否则输出 \\(-1\\) 。
输入格式
输入共 \\(n + m\\) 行,第一行为两个正整数 \\(n,m\\)。
后面 \\(n − 1\\) 行,每行两个正整数 \\(x_i,y_i\\) 表示第 \\(i\\) 条边的两个端点。
后面 \\(m\\) 行,每行两个正整数 \\(a_i,b_i\\) 。
对于 \\(30\\%\\) 的数据,保证 \\(1 < n ≤ 1000\\)。
对于 \\(100\\%\\) 的数据,保证 \\(1 < n ≤ 100000,1 ≤ m ≤ n / 2\\) 。
输出格式
一行一个整数,表示答案,如有多个答案,输出编号最大的一个。
输入样例
6 2
1 2
2 3
4 3
2 5
6 5
3 6
4 5
输出样例
4
断开第 2 条边后形成两个连通块:3, 4,1, 2, 5, 6,满足 3 和 6 不连通,4 和 5 不连通。
断开第 4 条边后形成两个连通块:1, 2, 3, 4,5, 6,同样满足 3 和 6 不连通,4 和 5 不连通。
4 编号更大,因此答案为 4。
思路
$LCA + $树上差分模板题,若砍掉某条边让这两点不连通,那么这条边一定是从 \\(x\\) 到 \\(y\\) 路径上的一点,我们可以利用树上差分,让 \\(diff[x]+1,diff[y]+1,diff[lca(x,y)]-2\\) ,最后做一遍 \\(dfs\\) 求和,让从 \\(x\\) 到 \\(y\\) 路径的边权值都加1,只需要从编号最大的倒序遍历,若存在一条边的值为 \\(m\\),则该边即为所求答案。若不存在,则输出 \\(-1\\)
代码
#include<bits/stdc++.h>
#define x first
#define y second;
using namespace std;
const int N=1e5+10,M=N*2;
typedef pair<int,int>PII;
int h[N],e[M],ne[M],idx;
int depth[N];//记录深度
int f[N][20];
int diff[N];//差分数组
PII edge[N];//记录每条边的编号
int n,m;
void add(int a,int b)
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
void dfs(int u,int fa)
depth[u]=depth[fa]+1;
f[u][0]=fa;
for(int i=1;i<=19;i++)
f[u][i]=f[f[u][i-1]][i-1];
for(int i=h[u];i!=-1;i=ne[i])
int j=e[i];
if(j!=fa)
dfs(j,u);
//倍增法求lca
int lca(int a,int b)
if(depth[a]<depth[b])swap(a,b);
for(int i=19;i>=0;i--)
if(depth[f[a][i]]>=depth[b])
a=f[a][i];
if(a==b)return a;
for(int i=19;i>=0;i--)
if(f[a][i]!=f[b][i])
a=f[a][i],b=f[b][i];
return f[a][0];
//利用dfs对树上的差分数组求和
void dfs1(int u,int fa)
for(int i=h[u];i!=-1;i=ne[i])
int j=e[i];
if(j!=fa)
dfs1(j,u);
diff[u]+=diff[j];
int main()
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=1;i<n;i++)
int a,b;
cin>>a>>b;
edge[i]=a,b;
add(a,b),add(b,a);
dfs(1,0);
for(int i=0;i<m;i++)
int a,b;
cin>>a>>b;
int p=lca(a,b);
diff[a]++,diff[b]++;
diff[p]-=2;
dfs1(1,0);
int res=-1;
for(int i=n-1;i>=1;i--)
int a=edge[i].x,b=edge[i].y;
if(depth[a]<depth[b])swap(a,b);//边的权值保存在深度大的节点上
if(diff[a]==m)
res=i;
break;
cout<<res<<endl;
return 0;
Java第六届蓝桥杯JAVA组B组省赛题解
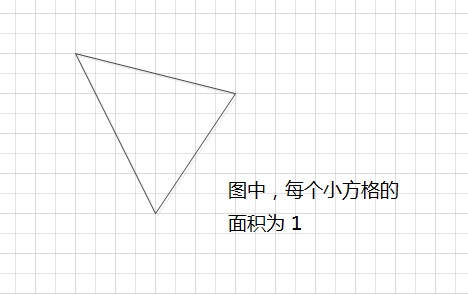
三角形面积
|
【题目描述】 如【图1】所示。图中的所有小方格面积都是1。 请填写三角形的面积。不要填写任何多余内容或说明性文字。
【知识点涉及】 【分析与解答】 【代码设计】 |
立方变自身
|
【题目描述】 【知识点涉及】 【分析与解答】 【代码设计】 |
三羊献瑞
|
【题目描述】 【知识点涉及】 【分析与解答】 【代码设计】 |
循环节长度
|
【题目描述】 【知识点涉及】 【分析与解答】 【代码设计】 |
九数组分数
|
【题目描述】 【知识点涉及】 【分析与解答】 【代码设计】 |
牌型种数
|
【题目描述】 【知识点涉及】 【分析与解答】 【代码设计】 |
加法变乘法
|
【题目描述】 【知识点涉及】 【分析与解答】 【代码设计】 |
饮料换购
|
【题目描述】 【知识点涉及】 【分析与解答】 【代码设计】 |
垒骰子
|
【题目描述】 【知识点涉及】 【分析与解答】 【代码设计】 |
生命之树
|
【题目描述】 【知识点涉及】 【分析与解答】 【代码设计】 |
以上是关于第14届蓝桥杯C++B组省赛题解(A-J)(更新完毕)的主要内容,如果未能解决你的问题,请参考以下文章