做8点的FFT程序 用C或matlab实现

Posted 2023-04-24

做8点的FFT程序 用C或matlab实现 我要具体的程序 思路不要

参考技术A n年前做的了基2的
#include "stdafx.h"
#include "complex.h"

void main()

const double pi = 3.14159265;
int i; //循环变量
//////////////////////////////////////////////////////////////////
//信号生成：正弦信号，固定频率。生成1024点
const N = 64; //信号点数
const n =N/2; //半点数，用于循环控制
float S[N]; //信号数组
float temp;
temp = (float) (8 * pi) / N; //出现两个周期
for(i=0; i<N; i++) S[i] = (float) sin(temp * i);
//////////////////////////////////////////////////////////////////
//旋转因子数组生成
complex W[n];
temp = (float) (2 * pi / N);
for(i=0; i<n; i++)
W[i].SetReal((float)cos(temp * i));
W[i].SetImag((float)-sin(temp * i));
// cout<<W[i]<<endl;

///////////////////////////////////////////////////////////////////
//变换：基2－FFT
//先做蝶形运算，再对信号排序
///////////////////////////////////////////////////////////////////

///////////////////////////////////////////////////////////////////
//读入排序的信号
complex* x;
x = new complex[N*sizeof(complex)];//计算用数组
///////////////////////////////////////////////////////////////////
//读入信号
for(i=0; i<N; i++) x[i].SetReal(S[i]);
///////////////////////////////////////////////////////////////////
//蝶形运算
int j, k; //循环变量
complex t;
for(i=n, k=1; i>=1; i>>=1, k<<=1)
k %= n; //旋转因子调整
for(j=0; j<N;)
t = x[j+i]; //蝶形运算
x[j+i] = x[j] - t;
x[j] = x[j] + t;
x[j+i] = x[j+i] * W[(j%i)*k];
j++;
if((j%i) == 0) j += i; //交叉


/////////////////////////////////////////////////////////////////////
//生成（以8点为例）形如0，4，2，6，1，5，3，7的排序数组
int* y;
y = new int[N*sizeof(int)]; //调整计算用数组的排序用数组
for(i=0; i<N; i++) y[i] = 0;
for(i=1, k=n; i<=n; i<<=1, k>>=1)
for(j=0; j<2*i; j++) y[i+j] = y[j] + k;
//////////////////////////////////////////////////////////////////////
//排序
complex* X;
X = new complex[N*sizeof(complex)];
for(i=0; i<N; i++) X[y[i]] = x[i];
delete [] x; //销毁运算数组
delete [] y; //销毁排序数组
////////////////////////////////////////////////////////////////////////
//归一化
float a[N];
for(i=0; i<N; i++) a[i] = X[i].mod();
delete [] X;
temp = a[0];
for(i=1; i<N; i++) if(a[i]>temp) temp = a[i];
for(i=0; i<N; i++) a[i] =(float) a[i] / temp;
for(i=0; i<N; i+=4) cout<<a[i]<<" "<<a[i+1]<<" "<<a[i+2]<<" "<<a[i+3]<<endl;

Matlab学习（用matlab进行fft谐波分析）

用matlab进行fft谐波分析

      FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外，FFT可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。

      虽然很多人都知道FFT是什么，可以用来做什么，怎么去做，但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。

      现在就根据实际经验来说说FFT结果的具体物理意义。一个模拟信号，经过ADC采样之后，就变成了数字信号。采样定理告诉我们，采样频率要大于信号频率的两倍，这些我就不在此罗嗦了。

      采样得到的数字信号，就可以做FFT变换了。N个采样点，经过FFT之后，就可以得到N个点的FFT结果。为了方便进行FFT运算，通常N取2的整数次方。

      假设采样频率为Fs，信号频率F，采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。而第一个点就是直流分量，它的模值就是直流分量的N倍。而每个点的相位呢，就是在该频率下的信号的相位。第一个点表示直流分量（即0Hz），而最后一个点N的再下一个点（实际上这个点是不存在的，这里是假设的第N+1个点，也可以看做是将第一个点分做两半分，另一半移到最后）则表示采样频率Fs，这中间被N-1个点平均分成N等份，每个点的频率依次增加。例如某点n所表示的频率为：Fn=(n-1)*Fs/N。由上面的公式可以看出，Fn所能分辨到频率为为Fs/N，如果采样频率Fs为1024Hz，采样点数为1024点，则可以分辨到1Hz。1024Hz的采样率采样1024点，刚好是1秒，也就是说，采样1秒时间的信号并做FFT，则结果可以分析到1Hz，如果采样2秒时间的信号并做FFT，则结果可以分析到0.5Hz。如果要提高频率分辨力，则必须增加采样点数，也即采样时间。频率分辨率和采样时间是倒数关系。

      假设FFT之后某点n用复数a+bi表示，那么这个复数的模就是An=根号a*a+b*b，相位就是Pn=atan2(b,a)。根据以上的结果，就可以计算出n点（n≠1，且n<=N/2）对应的信号的表达式为：An/(N/2)*cos(2*pi*Fn*t+Pn)，即2*An/N*cos(2*pi*Fn*t+Pn)。对于n=1点的信号，是直流分量，幅度即为A1/N。

      由于FFT结果的对称性，通常我们只使用前半部分的结果，即小于采样频率一半的结果。

      下面以一个实际的信号来做说明。

      假设我们有一个信号，它含有2V的直流分量，频率为50Hz、相位为-30度、幅度为3V的交流信号，以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下：

S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)

式中cos参数为弧度，所以-30度和90度要分别换算成弧度。我们以256Hz的采样率对这个信号进行采样，总共采样256点。按照我们上面的分析，Fn=(n-1)*Fs/N，我们可以知道，每两个点之间的间距就是1Hz，第n个点的频率就是n-1。我们的信号有3个频率：0Hz、50Hz、75Hz，应该分别在第1个点、第51个点、第76个点上出现峰值，其它各点应该接近0。实际情况如何呢？我们来看看FFT的结果的模值如图所示。

 

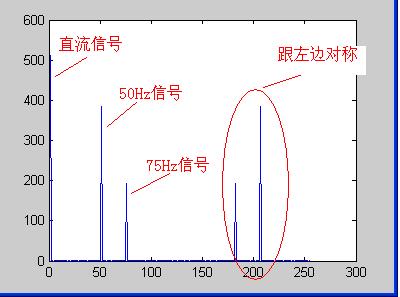
图1 FFT结果

      从图中我们可以看到，在第1点、第51点、和第76点附近有比较大的值。我们分别将这三个点附近的数据拿上来细看：

1点： 512+0i

2点： -2.6195E-14 - 1.4162E-13i

3点： -2.8586E-14 - 1.1898E-13i

50点：-6.2076E-13 - 2.1713E-12i

51点：332.55 - 192i

52点：-1.6707E-12 - 1.5241E-12i

75点：-2.2199E-13 -1.0076E-12i

76点：3.4315E-12 + 192i

77点：-3.0263E-14 +7.5609E-13i

      很明显，1点、51点、76点的值都比较大，它附近的点值都很小，可以认为是0，即在那些频率点上的信号幅度为0。接着，我们来计算各点的幅度值。分别计算这三个点的模值，结果如下：

1点： 512

51点：384

76点：192

      按照公式，可以计算出直流分量为：512/N=512/256=2；50Hz信号的幅度为：384/(N/2)=384/(256/2)=3；75Hz信号的幅度为192/(N/2)=192/(256/2)=1.5。可见，从频谱分析出来的幅度是正确的。

      然后再来计算相位信息。直流信号没有相位可言，不用管它。先计算50Hz信号的相位，atan2(-192, 332.55)=-0.5236,结果是弧度，换算为角度就是180*(-0.5236)/pi=-30.0001。再计算75Hz信号的相位，atan2(192, 3.4315E-12)=1.5708弧度，换算成角度就是180*1.5708/pi=90.0002。可见，相位也是对的。根据FFT结果以及上面的分析计算，我们就可以写出信号的表达式了，它就是我们开始提供的信号。

      总结：假设采样频率为Fs，采样点数为N，做FFT之后，某一点n（n从1开始）表示的频率为：Fn=(n-1)*Fs/N；该点的模值除以N/2就是对应该频率下的信号的幅度（对于直流信号是除以N）；该点的相位即是对应该频率下的信号的相位。相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值，范围从-pi到pi。要精确到xHz，则需要采样长度为1/x秒的信号，并做FFT。要提高频率分辨率，就需要增加采样点数，这在一些实际的应用中是不现实的，需要在较短的时间内完成分析。解决这个问题的方法有频率细分法，比较简单的方法是采样比较短时间的信号，然后在后面补充一定数量的0，使其长度达到需要的点数，再做FFT，这在一定程度上能够提高频率分辨力。具体的频率细分法可参考相关文献。

      [附录：本测试数据使用的matlab程序]

close all; %先关闭所有图片

Adc=2;  %直流分量幅度

A1=3;   %频率F1信号的幅度

A2=1.5; %频率F2信号的幅度

F1=50;  %信号1频率(Hz)

F2=75;  %信号2频率(Hz)

Fs=256; %采样频率(Hz)

P1=-30; %信号1相位(度)

P2=90;  %信号相位(度)

N=256;  %采样点数

t=[0:1/Fs:N/Fs]; %采样时刻

%信号

S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180);

plot(S);%显示原始信号

title(\'原始信号\');

figure;

Y = fft(S,N); %做FFT变换

Ayy = (abs(Y)); %取模

plot(Ayy(1:N)); %显示原始的FFT模值结果

title(\'FFT 模值\');

figure;

Ayy=Ayy/(N/2);   %换算成实际的幅度

Ayy(1)=Ayy(1)/2;

F=([1:N]-1)*Fs/N; %换算成实际的频率值

plot(F(1:N/2),Ayy(1:N/2));   %显示换算后的FFT模值结果

title(\'幅度-频率曲线图\');

figure;

Pyy=[1:N/2];

for i="1:N/2"

Pyy(i)=phase(Y(i)); %计算相位

Pyy(i)=Pyy(i)*180/pi; %换算为角度

end;

plot(F(1:N/2),Pyy(1:N/2));   %显示相位图

title(\'相位-频率曲线图\')